Giao tiếp kỹ thuật số - Mã đường dây
A line codelà mã được sử dụng để truyền dữ liệu của tín hiệu kỹ thuật số qua đường truyền. Quá trình mã hóa này được lựa chọn để tránh chồng chéo và biến dạng tín hiệu như nhiễu giữa các ký hiệu.
Thuộc tính của mã hóa dòng
Sau đây là các thuộc tính của mã hóa dòng:
Khi mã hóa được thực hiện để làm cho nhiều bit hơn truyền trên một tín hiệu, băng thông được sử dụng sẽ giảm đi nhiều.
Đối với một băng thông nhất định, điện năng được sử dụng hiệu quả.
Xác suất lỗi giảm đi nhiều.
Phát hiện lỗi được thực hiện và lưỡng cực cũng có khả năng sửa chữa.
Mật độ quyền lực nhiều thuận lợi.
Nội dung thời gian là phù hợp.
Chuỗi dài của 1s và 0s được tránh để duy trì tính minh bạch.
Các loại mã hóa dòng
Có 3 loại mã hóa dòng
- Unipolar
- Polar
- Bi-polar
Tín hiệu đơn cực
Tín hiệu đơn cực còn được gọi là On-Off Keying hoặc đơn giản OOK.
Sự hiện diện của xung thể hiện một 1 và sự vắng mặt của xung thể hiện một 0.
Có hai biến thể trong tín hiệu đơn cực -
- Non Return to Zero (NRZ)
- Trở về số không (RZ)
Đơn cực Không trở về 0 (NRZ)
Trong loại tín hiệu đơn cực này, Dữ liệu cao được biểu thị bằng một xung dương được gọi là Mark, có thời hạn T0bằng thời lượng bit ký hiệu. Đầu vào dữ liệu Thấp không có xung.
Hình dưới đây mô tả rõ ràng điều này.
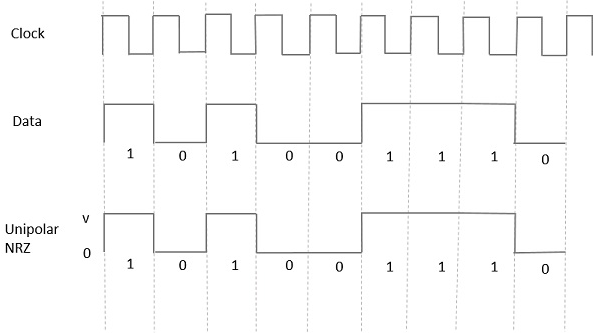
Advantages
Ưu điểm của Unipolar NRZ là -
- Nó đơn giản.
- Yêu cầu băng thông nhỏ hơn.
Disadvantages
Nhược điểm của NRZ đơn cực là -
Không sửa lỗi được thực hiện.
Sự hiện diện của các thành phần tần số thấp có thể làm giảm tín hiệu.
Không có đồng hồ hiện tại.
Mất đồng bộ hóa có thể xảy ra (đặc biệt là đối với các chuỗi dài 1s và 0s).
Đơn cực trở về 0 (RZ)
Trong loại tín hiệu đơn cực này, Dữ liệu cao, mặc dù được biểu thị bằng Mark pulse, thời hạn của nó T0nhỏ hơn thời lượng bit ký hiệu. Một nửa thời lượng bit vẫn ở mức cao nhưng nó ngay lập tức trở về 0 và cho thấy sự vắng mặt của xung trong nửa thời lượng bit còn lại.
Nó được hiểu rõ ràng với sự trợ giúp của hình sau.
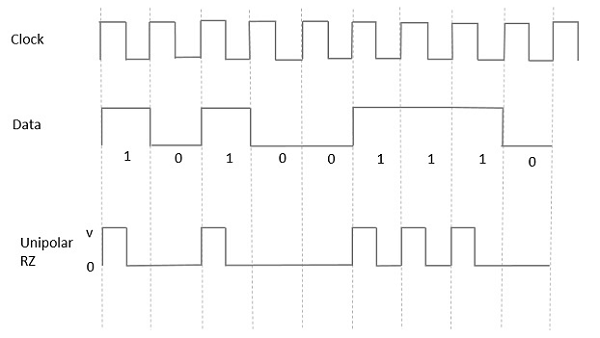
Advantages
Ưu điểm của RZ đơn cực là -
- Nó đơn giản.
- Vạch quang phổ có ở tỷ lệ ký hiệu có thể được sử dụng như một đồng hồ.
Disadvantages
Nhược điểm của RZ đơn cực là -
- Không sửa lỗi.
- Chiếm gấp đôi băng thông so với NRZ đơn cực.
- Sự sụt giảm tín hiệu được gây ra ở những nơi có tín hiệu khác 0 ở tần số 0 Hz.
Tín hiệu cực
Có hai phương pháp phát tín hiệu cực. Họ là -
- Polar NRZ
- Polar RZ
Polar NRZ
Trong loại tín hiệu Cực này, dữ liệu Cao được biểu thị bằng xung dương, trong khi dữ liệu Thấp được biểu thị bằng xung âm. Hình sau mô tả điều này tốt.
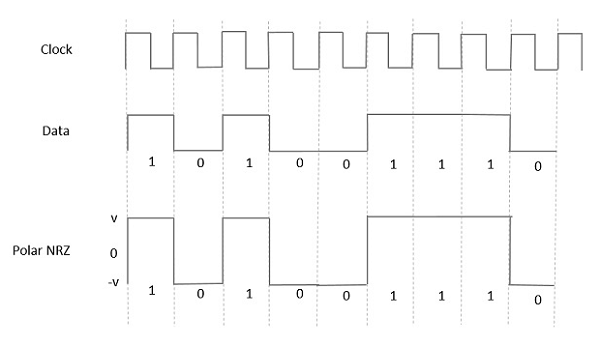
Advantages
Ưu điểm của Polar NRZ là -
- Nó đơn giản.
- Không có thành phần tần số thấp nào.
Disadvantages
Nhược điểm của Polar NRZ là -
Không sửa lỗi.
Không có đồng hồ hiện tại.
Sự sụt giảm tín hiệu được gây ra ở những nơi mà tín hiệu khác 0 tại 0 Hz.
Polar RZ
Trong loại báo hiệu Cực này, Dữ liệu cao, mặc dù được biểu thị bằng Mark pulse, thời hạn của nó T0nhỏ hơn thời lượng bit ký hiệu. Một nửa thời lượng bit vẫn ở mức cao nhưng nó ngay lập tức trở về 0 và cho thấy sự vắng mặt của xung trong nửa thời lượng bit còn lại.
Tuy nhiên, đối với đầu vào Thấp, một xung âm đại diện cho dữ liệu và mức 0 vẫn giữ nguyên trong nửa thời lượng bit còn lại. Hình dưới đây mô tả rõ điều này.
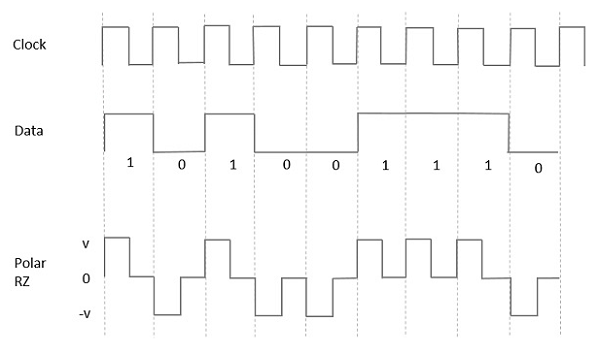
Advantages
Ưu điểm của Polar RZ là -
- Nó đơn giản.
- Không có thành phần tần số thấp nào.
Disadvantages
Nhược điểm của Polar RZ là -
Không sửa lỗi.
Không có đồng hồ hiện tại.
Chiếm gấp đôi băng thông của Polar NRZ.
Sự sụt giảm tín hiệu được gây ra ở những nơi mà tín hiệu khác 0 tại 0 Hz.
Tín hiệu lưỡng cực
Đây là một kỹ thuật mã hóa có ba mức điện áp cụ thể là +, - và 0. Một tín hiệu như vậy được gọi làduo-binary signal.
Một ví dụ của loại này là Alternate Mark Inversion (AMI). Cho một1, mức điện áp được chuyển đổi từ + sang - hoặc từ - sang +, có 1scó cực tính bằng nhau. A0 sẽ có mức điện áp bằng không.
Ngay cả trong phương pháp này, chúng tôi có hai loại.
- NRZ lưỡng cực
- RZ lưỡng cực
Từ các mô hình đã thảo luận cho đến nay, chúng tôi đã học được sự khác biệt giữa NRZ và RZ. Nó cũng diễn ra theo cùng một cách ở đây. Hình dưới đây mô tả rõ ràng điều này.
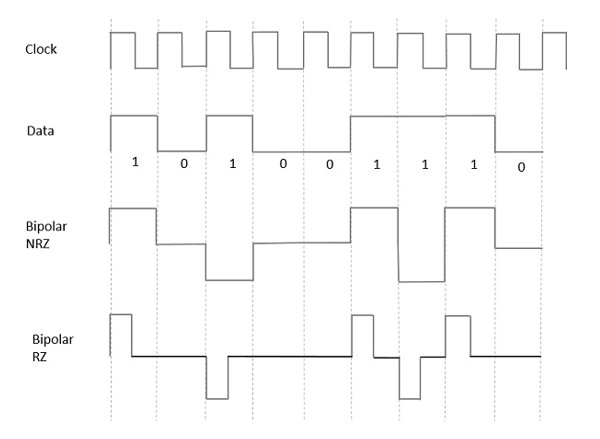
Hình trên có cả dạng sóng Bipolar NRZ và RZ. Thời lượng xung và thời lượng bit ký hiệu bằng nhau ở loại NRZ, trong khi thời lượng xung bằng một nửa thời lượng bit ký hiệu ở loại RZ.
Ưu điểm
Sau đây là những ưu điểm -
Nó đơn giản.
Không có thành phần tần số thấp nào.
Chiếm băng thông thấp hơn so với lược đồ NRZ đơn cực và cực.
Kỹ thuật này thích hợp để truyền qua các đường nối AC, vì tín hiệu không xảy ra ở đây.
Một khả năng phát hiện lỗi duy nhất có trong này.
Nhược điểm
Sau đây là những nhược điểm -
- Không có đồng hồ hiện tại.
- Chuỗi dữ liệu dài gây ra mất đồng bộ hóa.
Mật độ phổ công suất
Hàm mô tả cách sức mạnh của tín hiệu được phân phối ở các tần số khác nhau, trong miền tần số được gọi là Power Spectral Density (PSD).
PSD là Fourier Transform of Auto-Correlation (Sự tương đồng giữa các quan sát). Nó ở dạng xung hình chữ nhật.
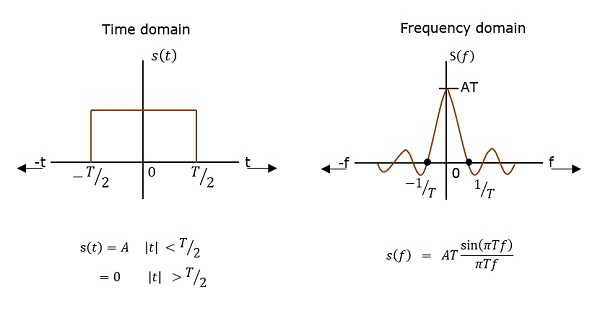
Nguồn gốc PSD
Theo định lý Einstein-Wiener-Khintchine, nếu biết hàm tương quan tự động hoặc mật độ phổ công suất của một quá trình ngẫu nhiên, thì quá trình kia có thể được tìm thấy chính xác.
Do đó, để tính mật độ phổ công suất, chúng ta sẽ sử dụng tương quan tự động theo thời gian $ (R_x (\ tau)) $ của tín hiệu công suất $ x (t) $ như hình dưới đây.
$ R_x (\ tau) = \ lim_ {T_p \ rightarrow \ infty} \ frac {1} {T_p} \ int _ {\ frac {{- T_p}} {2}} ^ {\ frac {T_p} {2}} x (t) x (t + \ tau) dt $
Vì $ x (t) $ bao gồm các xung, $ R_x (\ tau) $ có thể được viết là
$ R_x (\ tau) = \ frac {1} {T} \ displaystyle \ sum \ limit_ {n = - \ infty} ^ \ infty R_n \ delta (\ tau - nT) $
Trong đó $ R_n = \ lim_ {N \ rightarrow \ infty} \ frac {1} {N} \ sum_ka_ka_ {k + n} $
Nhận biết rằng $ R_n = R _ {- n} $ cho các tín hiệu thực, chúng tôi có
$ S_x (w) = \ frac {1} {T} (R_0 + 2 \ displaystyle \ sum \ limit_ {n = 1} ^ \ infty R_n \ cos nwT) $
Vì bộ lọc xung có phổ của $ (w) \ leftrightarrow f (t) $, chúng ta có
$ s_y (w) = \ mid F (w) \ mid ^ 2S_x (w) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (\ displaystyle \ sum \ limit_ {n = - \ infty} ^ \ infty R_ne ^ {- jnwT_ {b}}) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (R_0 + 2 \ displaystyle \ sum \ limit_ {n = 1} ^ \ infty R_n \ cos nwT) $
Do đó, chúng tôi nhận được phương trình cho Mật độ phổ công suất. Sử dụng điều này, chúng ta có thể tìm thấy PSD của nhiều mã dòng khác nhau.