Cầu AC
Trong chương này, chúng ta hãy thảo luận về cầu xoay chiều, có thể được sử dụng để đo độ tự cảm. Cầu xoay chiều chỉ hoạt động với tín hiệu điện áp xoay chiều. Cáccircuit diagram của cầu AC được hiển thị trong hình dưới đây.
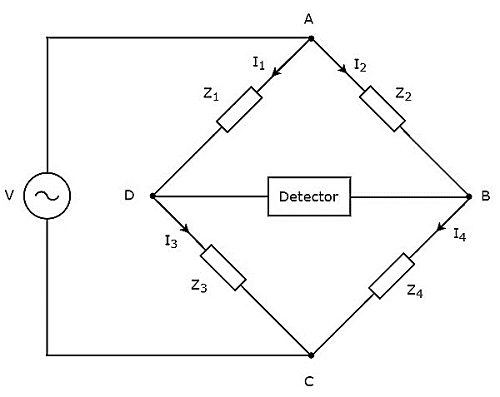
Như thể hiện trong hình trên, cầu xoay chiều chủ yếu bao gồm bốn nhánh, được kết nối theo hình thoi hoặc square shape. Tất cả các cánh tay này bao gồm một số trở kháng.
Bộ dò và nguồn điện áp xoay chiều cũng được yêu cầu để tìm giá trị của trở kháng chưa biết. Do đó, một trong hai chiếc này được đặt trên một đường chéo của cầu AC và chiếc còn lại được đặt ở đường chéo khác của cầu AC. Điều kiện cân bằng của cầu Wheatstone là -
$$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $$
Chúng tôi sẽ nhận được balancing condition of AC bridge, chỉ cần thay R bằng Z trong phương trình trên.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ \ Rightarrow Z_ {1} Z_ {4} = Z_ {2} Z_ {3} $
Ở đây, $ Z_ {1} $ và $ Z_ {2} $ là trở kháng cố định. Trong khi, $ Z_ {3} $ là trở kháng biến tiêu chuẩn và $ Z_ {4} $ là trở kháng không xác định.
Note - Chúng ta có thể chọn bất kỳ hai trong bốn trở kháng đó làm trở kháng cố định, một trở kháng làm trở kháng biến tiêu chuẩn & trở kháng còn lại làm trở kháng không xác định dựa trên ứng dụng.
Sau đây là hai cầu AC, có thể được sử dụng để đo inductance.
- Cầu Maxwell
- Cầu của Hay
Bây giờ, chúng ta hãy thảo luận về hai cầu AC này từng cái một.
Cầu Maxwell
Cầu Maxwell là cầu xoay chiều có bốn nhánh, được nối với nhau dưới dạng hình thoi hoặc square shape. Hai nhánh của cây cầu này bao gồm một điện trở duy nhất, một nhánh bao gồm một sự kết hợp nối tiếp của điện trở và cuộn cảm & nhánh còn lại bao gồm sự kết hợp song song của điện trở và tụ điện.
Một máy dò xoay chiều và nguồn điện áp xoay chiều được sử dụng để tìm giá trị của trở kháng chưa biết. Do đó, một trong hai cái này được đặt ở một đường chéo của cầu Maxwell và cái còn lại được đặt ở đường chéo khác của cầu Maxwell.
Cầu Maxwell được sử dụng để đo giá trị của điện cảm trung bình. Cáccircuit diagram của cầu Maxwell được hiển thị trong hình dưới đây.
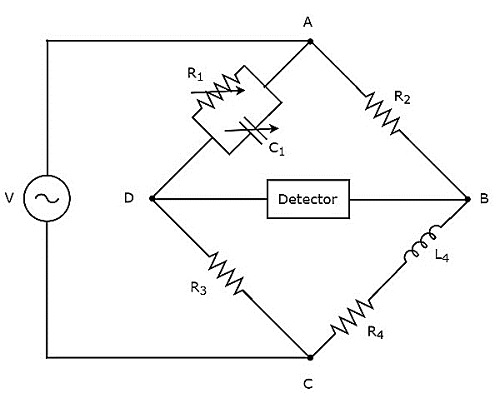
Trong đoạn mạch trên, các nhánh AB, BC, CD và DA cùng tạo thành hình thoi hoặc hình vuông. Các nhánh AB và CD gồm các điện trở, lần lượt là $ R_ {2} $ và $ R_ {3} $. Cánh tay, BC bao gồm một tổ hợp nối tiếp của điện trở, $ R_ {4} $ và cuộn cảm, $ L_ {4} $. Cánh tay, DA bao gồm sự kết hợp song song của điện trở, $ R_ {1} $ và tụ điện, $ C_ {1} $.
Gọi, $ Z_ {1}, Z_ {2}, Z_ {3} $ và $ Z_ {4} $ lần lượt là trở kháng của các nhánh DA, AB, CD và BC. Cácvalues of these impedances sẽ là
$$ Z_ {1} = \ frac {R_ {1} \ left (\ frac {1} {j \ omega C_ {1}} \ right)} {R_ {1} + \ frac {1} {j \ omega C_ {1}}} $$
$$ \ Rightarrow Z_ {1} = \ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}} $$
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute các giá trị trở kháng này trong điều kiện cân bằng sau của cầu xoay chiều.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left ({\ frac {R_ {1}} {1 + j \ omega R_ {1} C_ {1}}} \ right)} $$
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} \ left (1 + j \ omega R_ {1} C_ {1} \ right)} {R_ { 1}} đô la
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + \ frac {j \ omega R_ {1} C_ {1} R_ {2} R_ {3}} {R_ {1}} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} + j \ omega C_ {1} R_ {2} R_ {3} $
Bởi comparing các số hạng thực và ảo tương ứng của phương trình trên, chúng ta sẽ nhận được
$ R_ {4} = \ frac {R_ {2} R_ {3}} {R_ {1}} $ Phương trình 1
$ L_ {4} = C_ {1} R_ {2} R_ {3} $ Phương trình 2
Bằng cách thay các giá trị của điện trở $ R_ {1} $, $ R_ {2} $ và $ R_ {3} $ trong Phương trình 1, chúng ta sẽ nhận được giá trị của điện trở, $ R_ {4} $. Tương tự, bằng cách thay thế giá trị của tụ điện, $ C_ {1} $ và giá trị của điện trở, $ R_ {2} $ và $ R_ {3} $ trong Phương trình 2, chúng ta sẽ nhận được giá trị của cuộn cảm, $ L_ {4 } $.
Các advantage của cầu Maxwell là cả giá trị của điện trở, $ R_ {4} $ và cuộn cảm, $ L_ {4} $ đều độc lập với giá trị của tần số.
Cầu của Hay
Cầu của Hay là một phiên bản sửa đổi của cầu Maxwell, chúng tôi nhận được bằng cách sửa đổi nhánh, bao gồm sự kết hợp song song của điện trở và tụ điện vào nhánh, bao gồm một chuỗi kết hợp điện trở và tụ điện trong cầu Maxwell.
Cầu Hay dùng để đo giá trị của độ tự cảm cao. Cáccircuit diagram của cầu Hay được hiển thị trong hình dưới đây.
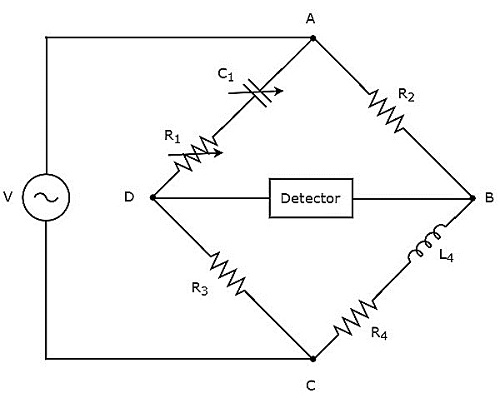
Trong đoạn mạch trên, các nhánh AB, BC, CD và DA cùng tạo thành hình thoi hoặc hình vuông. Các nhánh, AB và CD bao gồm các điện trở, lần lượt là $ R_ {2} $ và $ R_ {3} $. Cánh tay, BC bao gồm một tổ hợp nối tiếp của điện trở, $ R_ {4} $ và cuộn cảm, $ L_ {4} $. Phần nhánh, DA bao gồm một tổ hợp nối tiếp của điện trở, $ R_ {1} $ và tụ điện, $ C_ {1} $.
Gọi, $ Z_ {1}, Z_ {2}, Z_ {3} $ và $ Z_ {4} $ lần lượt là trở kháng của các nhánh DA, AB, CD và BC. Cácvalues of these impedances sẽ là
$$ Z_ {1} = R_ {1} + \ frac {1} {j \ omega C_ {1}} $$
$ \ Rightarrow Z_ {1} = \ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} $
$ Z_ {2} = R_ {2} $
$ Z_ {3} = R_ {3} $
$ Z_ {4} = R_ {4} + j \ omega L_ {4} $
Substitute các giá trị trở kháng này trong điều kiện cân bằng sau của cầu xoay chiều.
$$ Z_ {4} = \ frac {Z_ {2} Z_ {3}} {Z_ {1}} $$
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3}} {\ left (\ frac {1 + j \ omega R_ {1} C_ {1}} {j \ omega C_ {1}} \ right)} $
$ R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ {1} \ right)} $
Nhân tử số và mẫu số của số hạng bên phải của phương trình trên với $ 1 - j \ omega R_ {1} C_ {1} $.
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {R_ {2} R_ {3} j \ omega C_ {1}} {\ left (1 + j \ omega R_ {1} C_ { 1} \ right)} \ times \ frac {\ left (1 - j \ omega R_ {1} C_ {1} \ right)} {\ left (1 - j \ omega R_ {1} C_ {1} \ right )} $
$ \ Rightarrow R_ {4} + j \ omega L_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3} + j \ omega R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $
Bởi comparing các số hạng thực và ảo tương ứng của phương trình trên, chúng ta sẽ nhận được
$ R_ {4} = \ frac {\ omega ^ {2} {C_ {1}} ^ {2} R_ {1} R_ {2} R_ {3}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Phương trình 3
$ L_ {4} = \ frac {R_ {2} R_ {3} C_ {1}} {\ left (1+ \ omega ^ {2} {R_ {1}} ^ {2} {C_ {1}} ^ {2} \ right)} $ Phương trình 4
Bằng cách thay các giá trị của $ R_ {1}, R_ {2}, R_ {3}, C_ {1} $ và $ \ omega $ trong Phương trình 3 và Phương trình 4, chúng ta sẽ nhận được các giá trị của điện trở, $ R_ {4 } $ và cuộn cảm, $ L_ {4} $.