Kỹ thuật vi sóng - EH Plane Tee
Một điểm nối EH Plane Tee được hình thành bằng cách gắn hai ống dẫn sóng đơn giản song song và nối tiếp với một ống dẫn sóng hình chữ nhật đã có hai cổng. Điều này còn được gọi làMagic Tee, hoặc là Hybrid hoặc là 3dB coupler.
Các nhánh của ống dẫn sóng hình chữ nhật làm cho hai cổng được gọi là collinear ports tức là, Cổng 1 và Cổng 2, trong khi Cổng 3 được gọi là H-Arm hoặc là Sum port hoặc là Parallel port. Cổng 4 được gọi làE-Arm hoặc là Difference port hoặc là Series port.
Chi tiết mặt cắt của Magic Tee có thể được hiểu bằng hình sau.
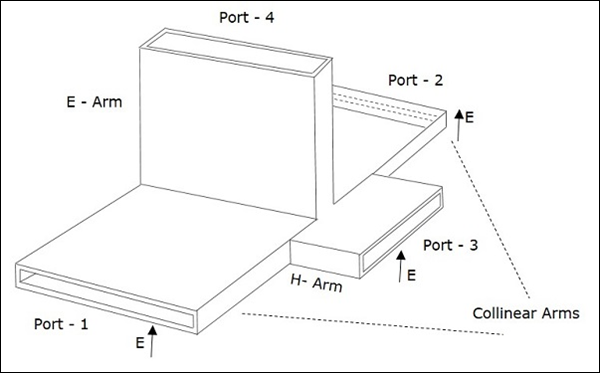
Hình dưới đây cho thấy kết nối được thực hiện bởi các nhánh bên với ống dẫn sóng hai chiều để tạo thành cả cổng song song và cổng nối tiếp.
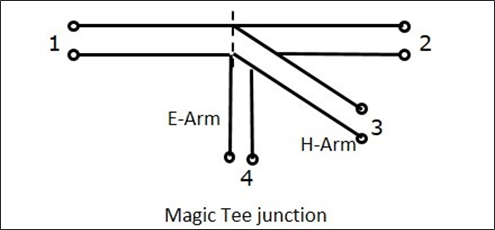
Đặc điểm của EH Plane Tee
Nếu một tín hiệu có độ lớn và pha bằng nhau được gửi đến cổng 1 và cổng 2, thì đầu ra ở cổng 4 bằng 0 và đầu ra ở cổng 3 sẽ là cộng của cả cổng 1 và 2.
Nếu tín hiệu được gửi đến cổng 4, (E-arm) thì nguồn được chia đều cho cổng 1 và 2 nhưng ngược pha, trong khi sẽ không có đầu ra ở cổng 3. Do đó, $ S_ {34} $ = 0 .
Nếu tín hiệu được cấp ở cổng 3, thì công suất được chia đều cho cổng 1 và 2, trong khi sẽ không có đầu ra ở cổng 4. Do đó, $ S_ {43} $ = 0.
Nếu một tín hiệu được cấp tại một trong các cổng thẳng hàng, thì sẽ không có đầu ra nào ở cổng thẳng hàng kia, vì nhánh E tạo ra trễ pha và nhánh H tạo ra trước pha. Vì vậy, $ S_ {12} $ = $ S_ {21} $ = 0.
Thuộc tính của EH Plane Tee
Các thuộc tính của EH Plane Tee có thể được xác định bởi ma trận $ \ left [S \ right] _ {4 \ times 4} $ của nó.
Nó là ma trận 4 × 4 vì có thể có 4 đầu vào và 4 đầu ra.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {21} & S_ {22} & S_ {23} & S_ {24} \\ S_ {31} & S_ {32} & S_ {33} & S_ {34} \\ S_ {41} & S_ {42} & S_ {43} & S_ {44} \ end {bmatrix} $ ........ Equation 1
Vì nó có phần H-Plane Tee
$ S_ {23} = S_ {13} $........ Equation 2
Vì nó có phần E-Plane Tee
$ S_ {24} = -S_ {14} $........ Equation 3
Cổng E-Arm và cổng H-Arm bị cô lập đến mức cổng còn lại sẽ không cung cấp đầu ra, nếu đầu vào được áp dụng tại một trong số chúng. Do đó, điều này có thể được lưu ý là
$ S_ {34} = S_ {43} = 0 $........ Equation 4
Từ tính chất đối xứng, chúng ta có
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21}, S_ {13} = S_ {31}, S_ {14} = S_ {41} $
$ S_ {23} = S_ {32}, S_ {24} = S_ {42}, S_ {34} = S_ {43} $........ Equation 5
Nếu cổng 3 và 4 hoàn toàn khớp với đường giao nhau, thì
$ S_ {33} = S_ {44} = 0 $........ Equation 6
Thay tất cả các phương trình trên vào phương trình 1, để thu được ma trận $ [S] $,
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {12} & S_ {22} & S_ {13} & -S_ {14 } \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} $........ Equation 7
Từ thuộc tính Nhất thể, $ [S] [S] ^ \ ast = [I] $
$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} & S_ {14} \\ S_ {12} & S_ {22} & S_ {13} & -S_ {14} \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} & S_ {14} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} & -S_ {14} ^ {*} \\ S_ {13} & S_ {13} & 0 & 0 \\ S_ {14} & -S_ {14} & 0 & 0 \ end {bmatrix} $
$ = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix} $
$ R_1C_1: \ còn lại | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 + \ left | S_ {14} \ right | ^ 2 = 1 $......... Equation 8
$ R_2C_2: \ trái | S_ {12} \ right | ^ 2 + \ left | S_ {22} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 + \ left | S_ {14} \ right | ^ 2 = 1 $......... Equation 9
$ R_3C_3: \ trái | S_ {13} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 10
$ R_4C_4: \ trái | S_ {14} \ right | ^ 2 + \ left | S_ {14} \ right | ^ 2 = 1 $......... Equation 11
Từ phương trình 10 và 11, chúng ta nhận được
$ S_ {13} = \ frac {1} {\ sqrt {2}} $........ Equation 12
$ S_ {14} = \ frac {1} {\ sqrt {2}} $........ Equation 13
So sánh phương trình 8 và 9, ta có
$ S_ {11} = S_ {22} $ ......... Equation 14
Sử dụng các giá trị này từ các phương trình 12 và 13, chúng tôi nhận được
$ \ còn lại | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 + \ frac {1} {2} + \ frac {1} {2} = 1 $
$ \ còn lại | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 = 0 $
$ S_ {11} = S_ {22} = 0 $ ......... Equation 15
Từ phương trình 9, chúng ta nhận được $ S_ {22} = 0 $ ......... Equation 16
Bây giờ chúng ta hiểu rằng cổng 1 và 2 hoàn toàn phù hợp với đường giao nhau. Vì đây là điểm giao nhau 4 cổng, bất cứ khi nào hai cổng khớp hoàn toàn, hai cổng còn lại cũng khớp hoàn hảo với điểm giao nhau.
Điểm giao nhau mà tất cả bốn cổng được kết hợp hoàn hảo được gọi là Magic Tee Junction.
Bằng cách thay thế các phương trình từ 12 đến 16, trong ma trận $ [S] $ của phương trình 7, chúng ta thu được ma trận tán xạ của Magic Tee là
$$ [S] = \ begin {bmatrix} 0 & 0 & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ 0 & 0 & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} {\ sqrt {2}} & 0 & 0 \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} {\ sqrt {2}} & 0 & 0 \ end {bmatrix} $$
Chúng tôi đã biết rằng, $ [b] $ = $ [S] [a] $
Viết lại những điều trên, chúng tôi nhận được
$$ \ begin {vmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \ end {vmatrix} = \ begin {bmatrix} 0 & 0 & \ frac {1} {2} & \ frac {1} {\ sqrt {2} } \\ 0 & 0 & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} {\ sqrt {2}} & 0 & 0 \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} {\ sqrt {2}} & 0 & 0 \ end {bmatrix} \ begin {vmatrix} a_1 \ \ a_2 \\ a_3 \\ a_4 \ end {vmatrix} $$
Các ứng dụng của EH Plane Tee
Một số ứng dụng phổ biến nhất của EH Plane Tee như sau:
Tiếp giáp EH Plane được sử dụng để đo trở kháng - Một đầu báo rỗng được kết nối với cổng E-Arm trong khi nguồn Vi sóng được kết nối với cổng H-Arm. Các cổng thẳng hàng cùng với các cổng này tạo thành một cầu nối và phép đo trở kháng được thực hiện bằng cách cân bằng cầu nối.
EH Plane Tee được sử dụng như một bộ song công - Bộ song công là một mạch hoạt động như một máy phát và máy thu, sử dụng một ăng-ten duy nhất cho cả hai mục đích. Cổng 1 và 2 được sử dụng làm bộ thu và phát nơi chúng được cách ly và do đó sẽ không gây nhiễu. Ăng-ten được kết nối với cổng E-Arm. Tải phù hợp được kết nối với cổng H-Arm, không cung cấp phản xạ. Bây giờ, có tồn tại truyền hoặc nhận mà không có bất kỳ vấn đề.
EH Plane Tee được sử dụng như một bộ trộn âm - Cổng E-Arm được kết nối với ăng-ten và cổng H-Arm được kết nối với bộ dao động cục bộ. Cổng 2 có tải phù hợp không có phản xạ và cổng 1 có mạch trộn, nhận một nửa công suất tín hiệu và một nửa công suất bộ dao động để tạo ra tần số IF.
Ngoài các ứng dụng trên, tiếp giáp EH Plane Tee còn được sử dụng làm cầu nối Vi sóng, Bộ phân biệt vi sóng, v.v.