Kỹ thuật vi sóng - H-Plane Tee
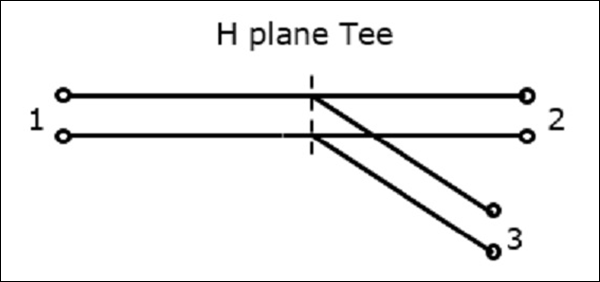
Tiếp giáp Tee mặt phẳng H được hình thành bằng cách gắn một ống dẫn sóng đơn giản vào một ống dẫn sóng hình chữ nhật đã có hai cổng. Các nhánh của ống dẫn sóng hình chữ nhật làm cho hai cổng được gọi làcollinear ports tức là, Port1 và Port2, trong khi cái mới, Port3 được gọi là Side arm hoặc H-arm. Tee mặt phẳng H này còn được gọi làShunt Tee.
Vì trục của cánh tay đòn song song với từ trường, đường giao nhau này được gọi là đường giao nhau H-Plane Tee. Điều này còn được gọi làCurrent junction, khi từ trường tự phân chia thành các nhánh. Các chi tiết về mặt cắt ngang của tee mặt phẳng H có thể được hiểu bằng hình sau.

Hình dưới đây cho thấy kết nối được thực hiện bởi sidearm với ống dẫn sóng hai chiều để tạo thành cổng nối tiếp.
Thuộc tính của Tăm mặt phẳng H
Các thuộc tính của H-Plane Tee có thể được xác định bởi ma trận $ \ left [S \ right] _ {3 \ times 3} $ của nó.
Nó là một ma trận 3 × 3 vì có thể có 3 đầu vào và 3 đầu ra có thể.
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1
Các hệ số tán xạ $ S_ {13} $ và $ S_ {23} $ ở đây bằng nhau vì đường giao nhau đối xứng trong mặt phẳng.
Từ tính chất đối xứng,
$ S_ {ij} = S_ {ji} $
$ S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} = S_ {13} \: \: S_ {13} = S_ {31} $
Cổng được kết hợp hoàn hảo
$ S_ {33} = 0 $
Bây giờ, ma trận $ [S] $ có thể được viết dưới dạng,
$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13 } & 0 \ end {bmatrix} $ ........ Equation 2
Chúng ta có thể nói rằng chúng ta có bốn ẩn số, xét tính chất đối xứng.
Từ thuộc tính Nhất thể
$$ [S] [S] \ ast = [I] $$
$$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & S_ {13} \\ S_ {13} & S_ {13} & 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & S_ {13} ^ {*} \\ S_ {13} ^ {*} & S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$
Nhân chúng ta nhận được,
(Lưu ý R là hàng và C là cột)
$ R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $
$ \ còn lại | S_ {11} \ right | ^ 2 + \ left | S_ {12} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $........ Equation 3
$ R_2C_2: \ trái | S_ {12} \ right | ^ 2 + \ left | S_ {22} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 4
$ R_3C_3: \ trái | S_ {13} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 5
$ R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 0 $ ......... Equation 6
$ 2 \ còn lại | S_ {13} \ right | ^ 2 = 1 \ quad hoặc \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 7
$ \ còn lại | S_ {11} \ right | ^ 2 = \ left | S_ {22} \ right | ^ 2 $
$ S_ {11} = S_ {22} $ ......... Equation 8
Từ phương trình 6, $ S_ {13} \ left (S_ {11} ^ {*} + S_ {12} ^ {*} \ right) = 0 $
Vì $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: hoặc \: S_ {11} ^ {*} = -S_ {12} ^ {*} $
Hoặc $ S_ {11} = -S_ {12} \: \: hoặc \: \: S_ {12} = -S_ {11} $......... Equation 9
Sử dụng chúng trong phương trình 3,
Vì $ S_ {13} \ neq 0, S_ {11} ^ {*} + S_ {12} ^ {*} = 0, \: hoặc \: S_ {11} ^ {*} = -S_ {12} ^ {*} $
$ \ còn lại | S_ {11} \ right | ^ 2 + \ left | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 \ quad hoặc \ quad 2 \ left | S_ {11} \ right | ^ 2 = \ frac {1} {2} \ quad hoặc \ quad S_ {11} = \ frac {1} {2} $..... Equation 10
Từ phương trình 8 và 9,
$ S_ {12} = - \ frac {1} {2} $......... Equation 11
$ S_ {22} = \ frac {1} {2} $......... Equation 12
Thay thế cho $ S_ {13} $, $ S_ {11} $, $ S_ {12} $ và $ S_ {22} $ từ phương trình 7 và 10, 11 và 12 trong phương trình 2,
Chúng tôi nhận được,
$$ \ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$
Chúng tôi biết rằng $ [b] $ = $ [s] [a] $
$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & - \ frac {1} {2} & \ frac {1} { \ sqrt {2}} \\ - \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt { 2}} & \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$
Đây là ma trận tán xạ cho H-Plane Tee, giải thích tính chất tán xạ của nó.