R - Hình vuông nhỏ nhất phi tuyến
Khi mô hình hóa dữ liệu thế giới thực để phân tích hồi quy, chúng tôi nhận thấy rằng hiếm khi xảy ra trường hợp phương trình của mô hình là một phương trình tuyến tính đưa ra một đồ thị tuyến tính. Hầu hết thời gian, phương trình của mô hình dữ liệu thế giới thực liên quan đến các hàm toán học ở mức độ cao hơn như số mũ của 3 hoặc hàm sin. Trong trường hợp như vậy, biểu đồ của mô hình là một đường cong chứ không phải là một đường thẳng. Mục tiêu của cả hồi quy tuyến tính và phi tuyến tính là điều chỉnh các giá trị của các tham số của mô hình để tìm đường hoặc đường cong gần nhất với dữ liệu của bạn. Khi tìm các giá trị này, chúng tôi sẽ có thể ước tính biến phản hồi với độ chính xác tốt.
Trong hồi quy Least Square, chúng tôi thiết lập một mô hình hồi quy trong đó tổng bình phương của các khoảng cách dọc của các điểm khác nhau từ đường cong hồi quy được tối thiểu hóa. Chúng tôi thường bắt đầu với một mô hình được xác định và giả định một số giá trị cho các hệ số. Sau đó, chúng tôi áp dụngnls() hàm của R để nhận các giá trị chính xác hơn cùng với khoảng tin cậy.
Cú pháp
Cú pháp cơ bản để tạo một phép thử bình phương nhỏ nhất phi tuyến trong R là:
nls(formula, data, start)Sau đây là mô tả về các tham số được sử dụng:
formula là một công thức mô hình phi tuyến bao gồm các biến và tham số.
data là khung dữ liệu dùng để đánh giá các biến trong công thức.
start là một danh sách được đặt tên hoặc vectơ số được đặt tên của các ước tính bắt đầu.
Thí dụ
Chúng ta sẽ xem xét một mô hình phi tuyến với giả định các giá trị ban đầu của các hệ số của nó. Tiếp theo, chúng ta sẽ xem khoảng tin cậy của các giá trị giả định này là gì để chúng ta có thể đánh giá mức độ ảnh hưởng của các giá trị này vào mô hình.
Vì vậy, hãy xem xét phương trình dưới đây cho mục đích này -
a = b1*x^2+b2Hãy giả sử các hệ số ban đầu là 1 và 3 và phù hợp với các giá trị này vào hàm nls ().
xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)
# Give the chart file a name.
png(file = "nls.png")
# Plot these values.
plot(xvalues,yvalues)
# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))
# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))
# Save the file.
dev.off()
# Get the sum of the squared residuals.
print(sum(resid(model)^2))
# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))Khi chúng tôi thực thi đoạn mã trên, nó tạo ra kết quả sau:
[1] 1.081935
Waiting for profiling to be done...
2.5% 97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484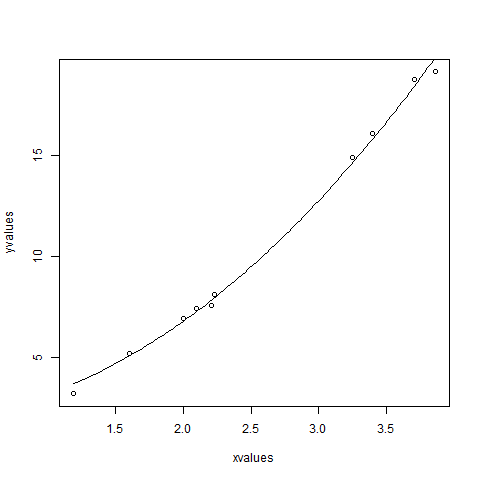
Chúng ta có thể kết luận rằng giá trị của b1 gần 1 hơn trong khi giá trị của b2 gần 2 hơn chứ không phải 3.