KI mit Python - Überwachtes Lernen: Klassifizierung

In diesem Kapitel konzentrieren wir uns auf die Implementierung der überwachten Lernklassifizierung.

Die Klassifizierungstechnik oder das Klassifizierungsmodell versucht, aus den beobachteten Werten eine Schlussfolgerung zu ziehen. Im Klassifizierungsproblem haben wir die kategorisierten Ausgaben wie "Schwarz" oder "Weiß" oder "Lehren" und "Nicht-Lehren". Beim Erstellen des Klassifizierungsmodells benötigen wir einen Trainingsdatensatz, der Datenpunkte und die entsprechenden Beschriftungen enthält. Zum Beispiel, wenn wir überprüfen möchten, ob das Bild von einem Auto ist oder nicht. Um dies zu überprüfen, erstellen wir einen Trainingsdatensatz mit den beiden Klassen „Auto“ und „Kein Auto“. Dann müssen wir das Modell anhand der Trainingsmuster trainieren. Die Klassifizierungsmodelle werden hauptsächlich zur Gesichtserkennung, Spam-Identifizierung usw. verwendet.

Schritte zum Erstellen eines Klassifikators in Python

Zum Erstellen eines Klassifikators in Python verwenden wir Python 3 und Scikit-learn, ein Werkzeug für maschinelles Lernen. Führen Sie die folgenden Schritte aus, um einen Klassifizierer in Python zu erstellen.

Schritt 1 - Scikit-Learn importieren

Dies wäre der erste Schritt zum Erstellen eines Klassifikators in Python. In diesem Schritt installieren wir ein Python-Paket namens Scikit-learn, eines der besten Module für maschinelles Lernen in Python. Der folgende Befehl hilft uns beim Importieren des Pakets -

Import Sklearn

Schritt 2 - Importieren Sie den Datensatz von Scikit-learn

In diesem Schritt können wir mit dem Datensatz für unser Modell des maschinellen Lernens beginnen. Hier werden wir verwendenthe Brustkrebs Wisconsin Diagnostic Database. Der Datensatz enthält verschiedene Informationen zu Brustkrebstumoren sowie Klassifizierungskennzeichnungen vonmalignant oder benign. Der Datensatz enthält 569 Instanzen oder Daten zu 569 Tumoren und enthält Informationen zu 30 Attributen oder Merkmalen wie dem Radius des Tumors, der Textur, der Glätte und der Fläche. Mit Hilfe des folgenden Befehls können wir den Brustkrebs-Datensatz von Scikit-learn importieren:

from sklearn.datasets import load_breast_cancer

Mit dem folgenden Befehl wird nun das Dataset geladen.

data = load_breast_cancer()

Es folgt eine Liste wichtiger Wörterbuchschlüssel -

Klassifizierungsbezeichnungsnamen (Zielnamen)
Die tatsächlichen Beschriftungen (Ziel)
Die Attribut- / Feature-Namen (Feature-Namen)
Das Attribut (Daten)

Mit Hilfe des folgenden Befehls können wir nun neue Variablen für jeden wichtigen Informationssatz erstellen und die Daten zuweisen. Mit anderen Worten, wir können die Daten mit den folgenden Befehlen organisieren:

label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']

Um es klarer zu machen, können wir jetzt die Klassenbezeichnungen, die Bezeichnung der ersten Dateninstanz, unsere Feature-Namen und den Wert des Features mit Hilfe der folgenden Befehle drucken:

print(label_names)

Mit dem obigen Befehl werden die bösartigen bzw. gutartigen Klassennamen gedruckt. Es wird als Ausgabe unten angezeigt -

['malignant' 'benign']

Der folgende Befehl zeigt nun, dass sie den Binärwerten 0 und 1 zugeordnet sind. Hier steht 0 für bösartigen Krebs und 1 für gutartigen Krebs. Sie erhalten folgende Ausgabe:

print(labels[0])
0

Die beiden folgenden Befehle erzeugen die Merkmalsnamen und Merkmalswerte.

print(feature_names[0])
mean radius
print(features[0])
[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
  1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
  2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
  8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
  5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
  2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
  1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
  4.60100000e-01 1.18900000e-01]

Aus der obigen Ausgabe können wir erkennen, dass die erste Dateninstanz ein bösartiger Tumor ist, dessen Radius 1,7990000e + 01 beträgt.

Schritt 3 - Organisieren von Daten in Sets

In diesem Schritt teilen wir unsere Daten in zwei Teile, nämlich einen Trainingssatz und einen Testsatz. Das Aufteilen der Daten in diese Sätze ist sehr wichtig, da wir unser Modell an den unsichtbaren Daten testen müssen. Um die Daten in Mengen aufzuteilen, verfügt sklearn über eine Funktion namenstrain_test_split()Funktion. Mit Hilfe der folgenden Befehle können wir die Daten in diese Sätze aufteilen -

from sklearn.model_selection import train_test_split

Der obige Befehl importiert das train_test_splitDie Funktion von sklearn und der folgende Befehl teilen die Daten in Trainings- und Testdaten auf. In dem unten angegebenen Beispiel verwenden wir 40% der Daten zum Testen und die verbleibenden Daten würden zum Trainieren des Modells verwendet.

train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)

Schritt 4 - Erstellen des Modells

In diesem Schritt werden wir unser Modell bauen. Wir werden den Naive Bayes-Algorithmus zum Erstellen des Modells verwenden. Die folgenden Befehle können zum Erstellen des Modells verwendet werden:

from sklearn.naive_bayes import GaussianNB

Der obige Befehl importiert das GaussianNB-Modul. Mit dem folgenden Befehl können Sie nun das Modell initialisieren.

gnb = GaussianNB()

Wir werden das Modell trainieren, indem wir es mit gnb.fit () an die Daten anpassen.

model = gnb.fit(train, train_labels)

Schritt 5 - Bewertung des Modells und seiner Genauigkeit

In diesem Schritt werden wir das Modell bewerten, indem wir Vorhersagen zu unseren Testdaten treffen. Dann werden wir auch seine Genauigkeit herausfinden. Um Vorhersagen zu treffen, verwenden wir die Funktion Predict (). Der folgende Befehl hilft Ihnen dabei:

preds = gnb.predict(test)
print(preds)

[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 
 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 
 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 
 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 
 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 
 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 
 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]

Die obigen Reihen von Nullen und Einsen sind die vorhergesagten Werte für die Tumorklassen - bösartig und gutartig.

Nun durch Vergleichen der beiden Arrays nämlich test_labels und predskönnen wir die Genauigkeit unseres Modells herausfinden. Wir werden das benutzenaccuracy_score()Funktion zur Bestimmung der Genauigkeit. Betrachten Sie dazu den folgenden Befehl:

from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965

Das Ergebnis zeigt, dass der NaïveBayes-Klassifikator zu 95,17% genau ist.

Auf diese Weise können wir mit Hilfe der obigen Schritte unseren Klassifikator in Python erstellen.

Gebäudeklassifikator in Python erstellen

In diesem Abschnitt erfahren Sie, wie Sie einen Klassifikator in Python erstellen.

Naiver Bayes-Klassifikator

Naive Bayes ist eine Klassifikationstechnik, mit der Klassifikatoren nach dem Bayes-Theorem erstellt werden. Die Annahme ist, dass die Prädiktoren unabhängig sind. In einfachen Worten wird davon ausgegangen, dass das Vorhandensein eines bestimmten Merkmals in einer Klasse nicht mit dem Vorhandensein eines anderen Merkmals zusammenhängt. Um einen Naïve Bayes-Klassifikator zu erstellen, müssen wir die Python-Bibliothek namens scikit learn verwenden. Es gibt drei Arten von Naive Bayes-ModellenGaussian, Multinomial and Bernoulli unter scikit lernpaket.

Um ein Naïve Bayes-Klassifikatormodell für maschinelles Lernen zu erstellen, benötigen wir das folgende & Minus

Datensatz

Wir werden den Datensatz mit dem Namen Breast Cancer Wisconsin Diagnostic Database verwenden. Der Datensatz enthält verschiedene Informationen zu Brustkrebstumoren sowie Klassifizierungskennzeichnungen vonmalignant oder benign. Der Datensatz enthält 569 Instanzen oder Daten zu 569 Tumoren und enthält Informationen zu 30 Attributen oder Merkmalen wie dem Radius des Tumors, der Textur, der Glätte und der Fläche. Wir können diesen Datensatz aus dem sklearn-Paket importieren.

Naives Bayes-Modell

Für die Erstellung des Naive Bayes-Klassifikators benötigen wir ein Naive Bayes-Modell. Wie bereits erwähnt, werden drei Arten von Naive Bayes-Modellen genanntGaussian, Multinomial und Bernoulliunter scikit lernpaket. Im folgenden Beispiel verwenden wir das Gaußsche Naive Bayes-Modell.

Mit den oben genannten Informationen werden wir ein maschinelles Lernmodell von Naive Bayes erstellen, um anhand der Tumorinformationen vorherzusagen, ob ein Tumor bösartig oder gutartig ist oder nicht.

Zunächst müssen wir das sklearn-Modul installieren. Dies kann mit Hilfe des folgenden Befehls erfolgen:

Import Sklearn

Jetzt müssen wir den Datensatz mit dem Namen Breast Cancer Wisconsin Diagnostic Database importieren.

from sklearn.datasets import load_breast_cancer

Mit dem folgenden Befehl wird nun das Dataset geladen.

data = load_breast_cancer()

Die Daten können wie folgt organisiert werden:

label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']

Um es klarer zu machen, können wir jetzt die Klassenbezeichnungen, die Bezeichnung der ersten Dateninstanz, unsere Feature-Namen und den Wert des Features mit Hilfe der folgenden Befehle drucken:

print(label_names)

Mit dem obigen Befehl werden die bösartigen bzw. gutartigen Klassennamen gedruckt. Es wird als Ausgabe unten angezeigt -

['malignant' 'benign']

Der folgende Befehl zeigt nun, dass sie den Binärwerten 0 und 1 zugeordnet sind. Hier steht 0 für bösartigen Krebs und 1 für gutartigen Krebs. Es wird als Ausgabe unten angezeigt -

print(labels[0])
0

Die folgenden zwei Befehle erzeugen die Merkmalsnamen und Merkmalswerte.

print(feature_names[0])
mean radius
print(features[0])

[ 1.79900000e+01 1.03800000e+01 1.22800000e+02 1.00100000e+03
  1.18400000e-01 2.77600000e-01 3.00100000e-01 1.47100000e-01
  2.41900000e-01 7.87100000e-02 1.09500000e+00 9.05300000e-01
  8.58900000e+00 1.53400000e+02 6.39900000e-03 4.90400000e-02
  5.37300000e-02 1.58700000e-02 3.00300000e-02 6.19300000e-03
  2.53800000e+01 1.73300000e+01 1.84600000e+02 2.01900000e+03
  1.62200000e-01 6.65600000e-01 7.11900000e-01 2.65400000e-01
  4.60100000e-01 1.18900000e-01]

Aus der obigen Ausgabe können wir erkennen, dass die erste Dateninstanz ein bösartiger Tumor ist, dessen Hauptradius 1,7990000e + 01 beträgt.

Um unser Modell auf unsichtbare Daten zu testen, müssen wir unsere Daten in Trainings- und Testdaten aufteilen. Dies kann mit Hilfe des folgenden Codes erfolgen:

from sklearn.model_selection import train_test_split

Der obige Befehl importiert das train_test_splitDie Funktion von sklearn und der folgende Befehl teilen die Daten in Trainings- und Testdaten auf. Im folgenden Beispiel verwenden wir 40% der Daten zum Testen und die verbleibenden Daten würden zum Trainieren des Modells verwendet.

train, test, train_labels, test_labels = 
train_test_split(features,labels,test_size = 0.40, random_state = 42)

Jetzt erstellen wir das Modell mit den folgenden Befehlen:

from sklearn.naive_bayes import GaussianNB

Der obige Befehl importiert das GaussianNBModul. Mit dem folgenden Befehl müssen wir nun das Modell initialisieren.

gnb = GaussianNB()

Wir werden das Modell trainieren, indem wir es mithilfe von an die Daten anpassen gnb.fit().

model = gnb.fit(train, train_labels)

Bewerten Sie nun das Modell, indem Sie die Testdaten vorhersagen. Dies kann wie folgt erfolgen:

preds = gnb.predict(test)
print(preds)

[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1
 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 
 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 0 0 
 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 
 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 
 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 
 1 1 0 1 1 1 1 1 1 0 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 
 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 0 0 1 1 0 1]

Die obigen Reihen von Nullen und Einsen sind die vorhergesagten Werte für die Tumorklassen, dh bösartig und gutartig.

from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965

Das Ergebnis zeigt, dass der NaïveBayes-Klassifikator zu 95,17% genau ist.

Das war ein Klassifikator für maschinelles Lernen, der auf dem Naïve Bayse Gaussian-Modell basierte.

Support Vector Machines (SVM)

Grundsätzlich ist Support Vector Machine (SVM) ein überwachter Algorithmus für maschinelles Lernen, der sowohl für die Regression als auch für die Klassifizierung verwendet werden kann. Das Hauptkonzept von SVM besteht darin, jedes Datenelement als Punkt im n-dimensionalen Raum darzustellen, wobei der Wert jedes Merkmals der Wert einer bestimmten Koordinate ist. Hier wären n die Funktionen, die wir hätten. Es folgt eine einfache grafische Darstellung, um das Konzept von SVM zu verstehen.

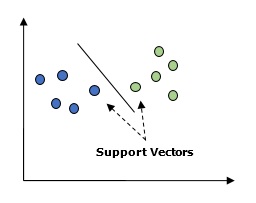
Im obigen Diagramm haben wir zwei Funktionen. Daher müssen wir diese beiden Variablen zunächst in einem zweidimensionalen Raum darstellen, in dem jeder Punkt zwei Koordinaten hat, die als Unterstützungsvektoren bezeichnet werden. Die Zeile teilt die Daten in zwei verschiedene klassifizierte Gruppen auf. Diese Zeile wäre der Klassifikator.

Hier erstellen wir einen SVM-Klassifikator unter Verwendung des Scikit-Learn- und Iris-Datasets. Scikitlearn Bibliothek hat diesklearn.svmModul und bietet sklearn.svm.svc zur Klassifizierung. Der SVM-Klassifikator zur Vorhersage der Klasse der Irispflanze basierend auf 4 Merkmalen ist unten gezeigt.

Datensatz

Wir werden den Iris-Datensatz verwenden, der 3 Klassen mit jeweils 50 Instanzen enthält, wobei sich jede Klasse auf eine Art Irispflanze bezieht. Jede Instanz hat die vier Merkmale, nämlich Kelchblattlänge, Kelchblattbreite, Blütenblattlänge und Blütenblattbreite. Der SVM-Klassifikator zur Vorhersage der Klasse der Irispflanze basierend auf 4 Merkmalen ist unten gezeigt.

Kernel

Es ist eine Technik, die von SVM verwendet wird. Grundsätzlich sind dies die Funktionen, die einen niedrigdimensionalen Eingaberaum in einen höherdimensionalen Raum umwandeln. Es konvertiert ein nicht trennbares Problem in ein trennbares Problem. Die Kernelfunktion kann eine beliebige zwischen linear, polynomial, rbf und sigmoid sein. In diesem Beispiel verwenden wir den linearen Kernel.

Importieren wir nun die folgenden Pakete -

import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as plt

Laden Sie nun die Eingabedaten -

iris = datasets.load_iris()

Wir nehmen die ersten beiden Funktionen -

X = iris.data[:, :2]
y = iris.target

Wir werden die Grenzen der Support-Vektor-Maschine mit den Originaldaten zeichnen. Wir erstellen ein Netz zum Plotten.

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]

Wir müssen den Wert des Regularisierungsparameters angeben.

C = 1.0

Wir müssen das SVM-Klassifikatorobjekt erstellen.

Svc_classifier = svm_classifier.SVC(kernel='linear', 
C=C, decision_function_shape = 'ovr').fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize = (15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap = plt.cm.tab10, alpha = 0.3)
plt.scatter(X[:, 0], X[:, 1], c = y, cmap = plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('SVC with linear kernel')

Logistische Regression

Grundsätzlich gehört das logistische Regressionsmodell zu den Mitgliedern der Familie der überwachten Klassifizierungsalgorithmen. Die logistische Regression misst die Beziehung zwischen abhängigen Variablen und unabhängigen Variablen, indem die Wahrscheinlichkeiten mithilfe einer logistischen Funktion geschätzt werden.

Wenn wir hier von abhängigen und unabhängigen Variablen sprechen, ist die abhängige Variable die Zielklassenvariable, die wir vorhersagen werden, und auf der anderen Seite sind die unabhängigen Variablen die Merkmale, die wir zur Vorhersage der Zielklasse verwenden werden.

Bei der logistischen Regression bedeutet das Schätzen der Wahrscheinlichkeiten, das Auftreten des Ereignisses mit Wahrscheinlichkeit vorherzusagen. Zum Beispiel möchte der Ladenbesitzer vorhersagen, dass der Kunde, der den Laden betreten hat, die Spielstation kaufen wird (zum Beispiel) oder nicht. Es gibt viele Merkmale des Kunden - Geschlecht, Alter usw., die vom Ladenbesitzer beobachtet werden, um die Wahrscheinlichkeit des Auftretens vorherzusagen, dh den Kauf einer Spielstation oder nicht. Die logistische Funktion ist die Sigmoidkurve, mit der die Funktion mit verschiedenen Parametern erstellt wird.

Voraussetzungen

Bevor wir den Klassifikator mithilfe der logistischen Regression erstellen, müssen wir das Tkinter-Paket auf unserem System installieren. Es kann von installiert werdenhttps://docs.python.org/2/library/tkinter.html.

Mit Hilfe des unten angegebenen Codes können wir nun einen Klassifikator mithilfe der logistischen Regression erstellen.

Zuerst werden wir einige Pakete importieren -

import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt

Nun müssen wir die Beispieldaten definieren, die wie folgt durchgeführt werden können:

X = np.array([[2, 4.8], [2.9, 4.7], [2.5, 5], [3.2, 5.5], [6, 5], [7.6, 4],
              [3.2, 0.9], [2.9, 1.9],[2.4, 3.5], [0.5, 3.4], [1, 4], [0.9, 5.9]])
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2, 3, 3, 3])

Als nächstes müssen wir den logistischen Regressionsklassifikator erstellen, der wie folgt ausgeführt werden kann:

Classifier_LR = linear_model.LogisticRegression(solver = 'liblinear', C = 75)

Last but not least müssen wir diesen Klassifikator trainieren -

Classifier_LR.fit(X, y)

Wie können wir nun die Ausgabe visualisieren? Dies kann durch Erstellen einer Funktion mit dem Namen Logistic_visualize () - erfolgen.

Def Logistic_visualize(Classifier_LR, X, y):
   min_x, max_x = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
   min_y, max_y = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0

In der obigen Zeile haben wir die Minimal- und Maximalwerte X und Y definiert, die im Netzgitter verwendet werden sollen. Zusätzlich definieren wir die Schrittgröße für das Zeichnen des Netzgitters.

mesh_step_size = 0.02

Definieren wir das Netzgitter der X- und Y-Werte wie folgt:

x_vals, y_vals = np.meshgrid(np.arange(min_x, max_x, mesh_step_size),
                 np.arange(min_y, max_y, mesh_step_size))

Mit Hilfe des folgenden Codes können wir den Klassifikator auf dem Netzgitter ausführen -

output = classifier.predict(np.c_[x_vals.ravel(), y_vals.ravel()])
output = output.reshape(x_vals.shape)
plt.figure()
plt.pcolormesh(x_vals, y_vals, output, cmap = plt.cm.gray)
 
plt.scatter(X[:, 0], X[:, 1], c = y, s = 75, edgecolors = 'black', 
linewidth=1, cmap = plt.cm.Paired)

Die folgende Codezeile gibt die Grenzen des Diagramms an

plt.xlim(x_vals.min(), x_vals.max())
plt.ylim(y_vals.min(), y_vals.max())
plt.xticks((np.arange(int(X[:, 0].min() - 1), int(X[:, 0].max() + 1), 1.0)))
plt.yticks((np.arange(int(X[:, 1].min() - 1), int(X[:, 1].max() + 1), 1.0)))
plt.show()

Nachdem wir den Code ausgeführt haben, erhalten wir den folgenden logistischen Regressionsklassifizierer für die Ausgabe:

Entscheidungsbaum-Klassifikator

Ein Entscheidungsbaum ist im Grunde ein Flussdiagramm eines binären Baums, in dem jeder Knoten eine Gruppe von Beobachtungen gemäß einer Merkmalsvariablen aufteilt.

Hier erstellen wir einen Entscheidungsbaumklassifikator zur Vorhersage von Männern oder Frauen. Wir werden einen sehr kleinen Datensatz mit 19 Proben nehmen. Diese Proben würden aus zwei Merkmalen bestehen - "Höhe" und "Haarlänge".

Voraussetzung

Um den folgenden Klassifikator zu erstellen, müssen wir installieren pydotplus und graphviz. Grundsätzlich ist graphviz ein Werkzeug zum Zeichnen von Grafiken mit Punktdateien undpydotplusist ein Modul zur Graphviz Dot-Sprache. Es kann mit dem Paketmanager oder pip installiert werden.

Jetzt können wir den Entscheidungsbaumklassifikator mit Hilfe des folgenden Python-Codes erstellen:

Lassen Sie uns zunächst einige wichtige Bibliotheken wie folgt importieren:

import pydotplus
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.metrics import classification_report
from sklearn import cross_validation
import collections

Jetzt müssen wir den Datensatz wie folgt bereitstellen:

X = [[165,19],[175,32],[136,35],[174,65],[141,28],[176,15],[131,32],
[166,6],[128,32],[179,10],[136,34],[186,2],[126,25],[176,28],[112,38],
[169,9],[171,36],[116,25],[196,25]]

Y = ['Man','Woman','Woman','Man','Woman','Man','Woman','Man','Woman',
'Man','Woman','Man','Woman','Woman','Woman','Man','Woman','Woman','Man']
data_feature_names = ['height','length of hair']

X_train, X_test, Y_train, Y_test = cross_validation.train_test_split
(X, Y, test_size=0.40, random_state=5)

Nach der Bereitstellung des Datensatzes müssen wir das Modell anpassen. Dies kann wie folgt erfolgen:

clf = tree.DecisionTreeClassifier()
clf = clf.fit(X,Y)

Die Vorhersage kann mit Hilfe des folgenden Python-Codes erfolgen:

prediction = clf.predict([[133,37]])
print(prediction)

Wir können den Entscheidungsbaum mit Hilfe des folgenden Python-Codes visualisieren:

dot_data = tree.export_graphviz(clf,feature_names = data_feature_names,
            out_file = None,filled = True,rounded = True)
graph = pydotplus.graph_from_dot_data(dot_data)
colors = ('orange', 'yellow')
edges = collections.defaultdict(list)

for edge in graph.get_edge_list():
edges[edge.get_source()].append(int(edge.get_destination()))

for edge in edges: edges[edge].sort()

for i in range(2):dest = graph.get_node(str(edges[edge][i]))[0]
dest.set_fillcolor(colors[i])
graph.write_png('Decisiontree16.png')

Es gibt die Vorhersage für den obigen Code als [‘Woman’] und erstellen Sie den folgenden Entscheidungsbaum -

Wir können die Werte von Merkmalen in der Vorhersage ändern, um sie zu testen.

Zufälliger Waldklassifikator

Wie wir wissen, sind Ensemble-Methoden die Methoden, die maschinelle Lernmodelle zu einem leistungsfähigeren maschinellen Lernmodell kombinieren. Random Forest, eine Sammlung von Entscheidungsbäumen, ist einer davon. Es ist besser als ein einzelner Entscheidungsbaum, da es unter Beibehaltung der Vorhersagekraft eine Überanpassung durch Mittelung der Ergebnisse reduzieren kann. Hier werden wir das Zufallswaldmodell auf Scikit Learn Cancer Dataset implementieren.

Importieren Sie die erforderlichen Pakete -

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
import matplotlib.pyplot as plt
import numpy as np

Jetzt müssen wir den Datensatz bereitstellen, der wie folgt ausgeführt werden kann & minus

cancer = load_breast_cancer()
X_train, X_test, y_train,
y_test = train_test_split(cancer.data, cancer.target, random_state = 0)

Nach der Bereitstellung des Datensatzes müssen wir das Modell anpassen. Dies kann wie folgt erfolgen:

forest = RandomForestClassifier(n_estimators = 50, random_state = 0)
forest.fit(X_train,y_train)

Holen Sie sich jetzt die Genauigkeit beim Training und beim Testen der Teilmenge: Wenn wir die Anzahl der Schätzer erhöhen, wird auch die Genauigkeit der Test-Teilmenge erhöht.

print('Accuracy on the training subset:(:.3f)',format(forest.score(X_train,y_train)))
print('Accuracy on the training subset:(:.3f)',format(forest.score(X_test,y_test)))

Ausgabe

Accuracy on the training subset:(:.3f) 1.0
Accuracy on the training subset:(:.3f) 0.965034965034965

Nun hat der zufällige Wald wie der Entscheidungsbaum die feature_importanceModul, das eine bessere Sicht auf das Feature-Gewicht bietet als der Entscheidungsbaum. Es kann wie folgt gezeichnet und visualisiert werden:

n_features = cancer.data.shape[1]
plt.barh(range(n_features),forest.feature_importances_, align='center')
plt.yticks(np.arange(n_features),cancer.feature_names)
plt.xlabel('Feature Importance')
plt.ylabel('Feature')
plt.show()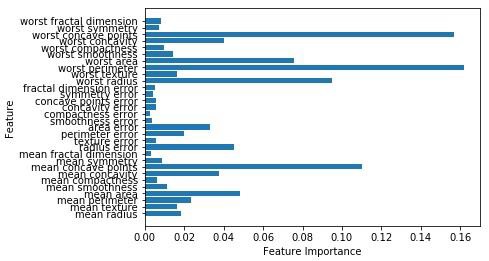

Leistung eines Klassifikators

Nach der Implementierung eines Algorithmus für maschinelles Lernen müssen wir herausfinden, wie effektiv das Modell ist. Die Kriterien zur Messung der Wirksamkeit können auf Datensätzen und Metriken basieren. Zur Bewertung verschiedener Algorithmen für maschinelles Lernen können wir verschiedene Leistungsmetriken verwenden. Angenommen, wenn ein Klassifizierer zur Unterscheidung zwischen Bildern verschiedener Objekte verwendet wird, können wir die Klassifizierungsleistungsmetriken wie Durchschnittsgenauigkeit, AUC usw. verwenden. In dem einen oder anderen Sinne ist die Metrik, die wir zur Bewertung unseres maschinellen Lernmodells auswählen Sehr wichtig, da die Auswahl der Metriken Einfluss darauf hat, wie die Leistung eines Algorithmus für maschinelles Lernen gemessen und verglichen wird. Im Folgenden sind einige der Metriken aufgeführt:

Verwirrung Matrix

Grundsätzlich wird es für Klassifizierungsprobleme verwendet, bei denen die Ausgabe aus zwei oder mehr Arten von Klassen bestehen kann. Dies ist der einfachste Weg, um die Leistung eines Klassifikators zu messen. Eine Verwirrungsmatrix ist im Grunde eine Tabelle mit zwei Dimensionen, nämlich "Ist" und "Vorausgesagt". Beide Dimensionen haben "True Positives (TP)", "True Negatives (TN)", "False Positives (FP)", "False Negatives (FN)".

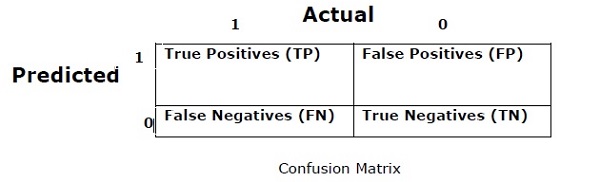
In der obigen Verwirrungsmatrix steht 1 für eine positive Klasse und 0 für eine negative Klasse.

Im Folgenden sind die mit der Verwirrungsmatrix verbundenen Begriffe aufgeführt:

True Positives − TPs sind die Fälle, in denen die tatsächliche Klasse des Datenpunkts 1 war und die vorhergesagte ebenfalls 1 ist.
True Negatives − TNs sind die Fälle, in denen die tatsächliche Klasse des Datenpunkts 0 war und die vorhergesagte ebenfalls 0 ist.
False Positives − FPs sind die Fälle, in denen die tatsächliche Klasse von Datenpunkten 0 war und die vorhergesagte ebenfalls 1 ist.
False Negatives − FNs sind die Fälle, in denen die tatsächliche Klasse des Datenpunkts 1 war und die vorhergesagte ebenfalls 0 ist.

Richtigkeit

Die Verwirrungsmatrix selbst ist kein Leistungsmaß als solches, aber fast alle Leistungsmatrizen basieren auf der Verwirrungsmatrix. Eine davon ist die Genauigkeit. Bei Klassifizierungsproblemen kann dies als die Anzahl der korrekten Vorhersagen definiert werden, die das Modell über alle Arten von Vorhersagen gemacht hat. Die Formel zur Berechnung der Genauigkeit lautet wie folgt:

$$ Genauigkeit = \ frac {TP + TN} {TP + FP + FN + TN} $$

Präzision

Es wird hauptsächlich beim Abrufen von Dokumenten verwendet. Es kann definiert werden, wie viele der zurückgegebenen Dokumente korrekt sind. Es folgt die Formel zur Berechnung der Genauigkeit -

$$ Präzision = \ frac {TP} {TP + FP} $$

Rückruf oder Empfindlichkeit

Es kann definiert werden, wie viele der positiven Ergebnisse das Modell zurückgibt. Es folgt die Formel zur Berechnung des Rückrufs / der Empfindlichkeit des Modells -

$$ Recall = \ frac {TP} {TP + FN} $$

Spezifität

Es kann definiert werden, wie viele der Negative das Modell zurückgibt. Es ist genau das Gegenteil zu erinnern. Es folgt die Formel zur Berechnung der Spezifität des Modells -

$$ Spezifität = \ frac {TN} {TN + FP} $$

Problem mit dem Klassenungleichgewicht

Das Klassenungleichgewicht ist das Szenario, in dem die Anzahl der Beobachtungen, die zu einer Klasse gehören, erheblich geringer ist als die der anderen Klassen. Dieses Problem tritt beispielsweise in dem Szenario auf, in dem seltene Krankheiten, betrügerische Bankgeschäfte usw. identifiziert werden müssen.

Beispiel für unausgeglichene Klassen

Betrachten wir ein Beispiel für einen Betrugserkennungsdatensatz, um das Konzept einer unausgeglichenen Klasse zu verstehen.

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

Lösung

Balancing the classes’wirkt als Lösung für unausgeglichene Klassen. Das Hauptziel des Klassenausgleichs besteht darin, entweder die Häufigkeit der Minderheitsklasse zu erhöhen oder die Häufigkeit der Mehrheitsklasse zu verringern. Im Folgenden sind die Ansätze zur Lösung des Problems der Ungleichgewichtsklassen aufgeführt:

Neuabtastung

Re-Sampling ist eine Reihe von Methoden zur Rekonstruktion der Probendatensätze - sowohl Trainingssätze als auch Testsätze. Eine erneute Probenahme wird durchgeführt, um die Genauigkeit des Modells zu verbessern. Im Folgenden finden Sie einige Techniken zur erneuten Probenahme.

Random Under-Sampling- Diese Technik zielt darauf ab, die Klassenverteilung auszugleichen, indem Beispiele für Mehrheitsklassen zufällig eliminiert werden. Dies geschieht so lange, bis die Instanzen der Mehrheits- und Minderheitsklasse ausgeglichen sind.

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

In diesem Fall nehmen wir 10% Proben ohne Ersatz aus nicht betrügerischen Instanzen und kombinieren sie dann mit den betrügerischen Instanzen.

Nicht betrügerische Beobachtungen nach zufälliger Stichprobe = 10% von 4950 = 495

Gesamtbeobachtungen nach Kombination mit betrügerischen Beobachtungen = 50 + 495 = 545

Daher beträgt jetzt die Ereignisrate für neuen Datensatz nach Unterabtastung = 9%

Der Hauptvorteil dieser Technik besteht darin, dass sie die Laufzeit reduzieren und die Speicherung verbessern kann. Auf der anderen Seite können jedoch nützliche Informationen verworfen und gleichzeitig die Anzahl der Trainingsdatenproben verringert werden.

Random Over-Sampling - Diese Technik zielt darauf ab, die Klassenverteilung auszugleichen, indem die Anzahl der Instanzen in der Minderheitsklasse durch Replikation erhöht wird.

Total observations = 5000
Fraudulent Observations = 50
Non-Fraudulent Observations = 4950
Event Rate = 1%

Wenn wir 50 betrügerische Beobachtungen 30 Mal replizieren, wären betrügerische Beobachtungen nach dem Replizieren der Beobachtungen der Minderheitenklasse 1500. Und dann wären die Gesamtbeobachtungen in den neuen Daten nach Überabtastung 4950 + 1500 = 6450. Daher die Ereignisrate für den neuen Datensatz wäre 1500/6450 = 23%.

Der Hauptvorteil dieser Methode besteht darin, dass keine nützlichen Informationen verloren gehen. Auf der anderen Seite besteht jedoch eine erhöhte Wahrscheinlichkeit einer Überanpassung, da die Ereignisse der Minderheitenklasse nachgebildet werden.

Ensemble-Techniken

Diese Methode wird im Wesentlichen verwendet, um vorhandene Klassifizierungsalgorithmen so zu ändern, dass sie für unausgeglichene Datensätze geeignet sind. Bei diesem Ansatz konstruieren wir mehrere zweistufige Klassifikatoren aus den Originaldaten und aggregieren dann ihre Vorhersagen. Der zufällige Waldklassifikator ist ein Beispiel für einen ensemblebasierten Klassifikator.