Datenstruktur und Algorithmen - AVL-Bäume
Was ist, wenn die Eingabe in den binären Suchbaum sortiert (aufsteigend oder absteigend) erfolgt? Es wird dann so aussehen -

Es wird beobachtet, dass die Worst-Case-Leistung von BST den linearen Suchalgorithmen am nächsten kommt, dh Ο (n). In Echtzeitdaten können wir das Datenmuster und ihre Häufigkeit nicht vorhersagen. Es besteht also die Notwendigkeit, die bestehende BST auszugleichen.
Benannt nach ihrem Erfinder Adelson, Velski & Landis, AVL treessind höhenausgleichende binäre Suchbaum. Der AVL-Baum überprüft die Höhe der linken und rechten Unterbäume und stellt sicher, dass der Unterschied nicht mehr als 1 beträgt. Dieser Unterschied wird als bezeichnetBalance Factor.
Hier sehen wir, dass der erste Baum ausgeglichen ist und die nächsten beiden Bäume nicht ausgeglichen sind -
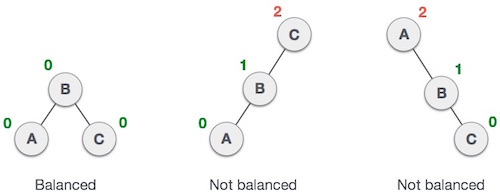
Im zweiten Baum der linke Teilbaum von C hat Höhe 2 und der rechte Teilbaum hat Höhe 0, der Unterschied ist also 2. Im dritten Baum ist der rechte Teilbaum von Ahat Höhe 2 und die linke fehlt, also ist es 0 und die Differenz ist wieder 2. Der AVL-Baum erlaubt, dass die Differenz (Ausgleichsfaktor) nur 1 beträgt.
BalanceFactor = height(left-sutree) − height(right-sutree)Wenn der Höhenunterschied zwischen linken und rechten Teilbäumen mehr als 1 beträgt, wird der Baum mithilfe einiger Rotationstechniken ausgeglichen.
AVL-Rotationen
Um sich selbst auszugleichen, kann ein AVL-Baum die folgenden vier Arten von Rotationen ausführen:
- Linksdrehung
- Rechtsdrehung
- Links-Rechts-Drehung
- Rechts-Links-Drehung
Die ersten beiden Umdrehungen sind Einzelumdrehungen und die nächsten beiden Umdrehungen sind Doppelumdrehungen. Um einen unausgeglichenen Baum zu haben, brauchen wir mindestens einen Baum der Höhe 2. Bei diesem einfachen Baum verstehen wir sie nacheinander.
Linksdrehung
Wenn ein Baum aus dem Gleichgewicht gerät und ein Knoten in den rechten Teilbaum des rechten Teilbaums eingefügt wird, führen wir eine einzelne Linksdrehung durch -

In unserem Beispiel Knoten Aist aus dem Gleichgewicht geraten, als ein Knoten in den rechten Teilbaum des rechten Teilbaums von A eingefügt wird. Wir führen die Linksdrehung durch, indem wir machenA der linke Teilbaum von B.
Rechtsdrehung
Der AVL-Baum kann aus dem Gleichgewicht geraten, wenn ein Knoten in den linken Teilbaum des linken Teilbaums eingefügt wird. Der Baum braucht dann eine Rechtsdrehung.

Wie dargestellt, wird der unausgeglichene Knoten durch Ausführen einer Rechtsdrehung zum rechten Kind seines linken Kindes.
Links-Rechts-Drehung
Doppelrotationen sind eine etwas komplexe Version bereits erklärter Versionen von Rotationen. Um sie besser zu verstehen, sollten wir jede Aktion notieren, die während der Rotation ausgeführt wird. Lassen Sie uns zunächst überprüfen, wie die Links-Rechts-Drehung durchgeführt wird. Eine Links-Rechts-Drehung ist eine Kombination aus Links- und Rechtsdrehung.
| Zustand | Aktion |
|---|---|

|
Ein Knoten wurde in den rechten Teilbaum des linken Teilbaums eingefügt. Das machtCein unausgeglichener Knoten. Diese Szenarien führen dazu, dass der AVL-Baum eine Links-Rechts-Drehung ausführt. |

|
Wir führen zuerst die Linksdrehung im linken Teilbaum von durch C. Das machtA, der linke Teilbaum von B. |

|
Knoten C ist immer noch unausgeglichen, aber jetzt liegt es am linken Teilbaum des linken Teilbaums. |

|
Wir werden jetzt den Baum nach rechts drehen und machen B der neue Wurzelknoten dieses Teilbaums. C Jetzt wird der rechte Teilbaum seines eigenen linken Teilbaums. |

|
Der Baum ist jetzt ausgeglichen. |
Rechts-Links-Drehung
Die zweite Art der Doppelrotation ist die Rechts-Links-Rotation. Es ist eine Kombination aus Rechtsdrehung und Linksdrehung.
| Zustand | Aktion |
|---|---|

|
Ein Knoten wurde in den linken Teilbaum des rechten Teilbaums eingefügt. Das machtAein unsymmetrischer Knoten mit Ausgleichsfaktor 2. |

|
Zuerst führen wir die richtige Drehung durch C Knoten machen C der rechte Teilbaum seines eigenen linken Teilbaums B. Jetzt,B wird der richtige Teilbaum von A. |

|
Knoten A ist aufgrund des rechten Teilbaums seines rechten Teilbaums immer noch unausgeglichen und erfordert eine Linksdrehung. |

|
Eine Linksdrehung wird durch Machen ausgeführt B der neue Wurzelknoten des Teilbaums. A wird der linke Teilbaum seines rechten Teilbaums B. |

|
Der Baum ist jetzt ausgeglichen. |