Heap-Datenstrukturen
Heap ist ein Sonderfall einer ausgeglichenen binären Baumdatenstruktur, bei der der Wurzelknotenschlüssel mit seinen untergeordneten Elementen verglichen und entsprechend angeordnet wird. Wennα hat untergeordneten Knoten β dann -
Schlüssel (α) ≥ Schlüssel (β)
Da der Wert von parent größer als der von child ist, wird diese Eigenschaft generiert Max Heap. Basierend auf diesen Kriterien kann ein Haufen von zwei Arten sein -
For Input → 35 33 42 10 14 19 27 44 26 31Min-Heap - Wenn der Wert des Wurzelknotens kleiner oder gleich einem seiner untergeordneten Knoten ist.
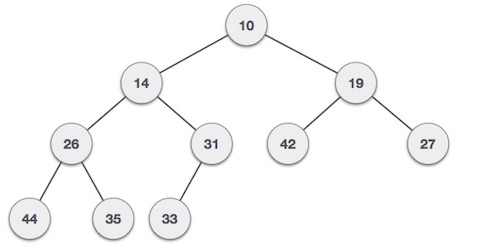
Max-Heap - Wenn der Wert des Wurzelknotens größer oder gleich einem seiner untergeordneten Knoten ist.

Beide Bäume werden mit derselben Eingabe und Ankunftsreihenfolge erstellt.
Max Heap Konstruktionsalgorithmus
Wir werden dasselbe Beispiel verwenden, um zu demonstrieren, wie ein Max Heap erstellt wird. Die Vorgehensweise zum Erstellen von Min Heap ist ähnlich, wir verwenden jedoch Min-Werte anstelle von Max-Werten.
Wir werden einen Algorithmus für den maximalen Heap ableiten, indem wir jeweils ein Element einfügen. Zu jedem Zeitpunkt muss der Heap sein Eigentum behalten. Beim Einfügen wird auch davon ausgegangen, dass wir einen Knoten in einen bereits Heapified-Baum einfügen.
Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.Note - Beim Min Heap-Konstruktionsalgorithmus erwarten wir, dass der Wert des übergeordneten Knotens kleiner als der des untergeordneten Knotens ist.
Lassen Sie uns die Max-Heap-Konstruktion anhand einer animierten Illustration verstehen. Wir betrachten das gleiche Eingabebeispiel, das wir zuvor verwendet haben.

Max Heap Deletion Algorithmus
Lassen Sie uns einen Algorithmus ableiten, der aus dem maximalen Heap gelöscht werden soll. Das Löschen im maximalen (oder minimalen) Heap erfolgt immer im Stammverzeichnis, um den maximalen (oder minimalen) Wert zu entfernen.
Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.