Elektronische Schaltungen - Vollweggleichrichter

Eine Gleichrichterschaltung, die sowohl die positiven als auch die negativen Halbzyklen gleichrichtet, kann als Vollweggleichrichter bezeichnet werden, da sie den gesamten Zyklus gleichrichtet. Der Aufbau eines Vollweggleichrichters kann in zwei Arten erfolgen. Sie sind

• Mittenabgriff-Vollweggleichrichter
• Brücken-Vollweggleichrichter

Beide haben ihre Vor- und Nachteile. Lassen Sie uns nun beide Konstruktionen durchgehen und mit ihren Wellenformen zusammenarbeiten, um herauszufinden, welche besser ist und warum.

Mittengewinde-Vollweggleichrichter

Eine Gleichrichterschaltung, deren Transformatorsekundär abgegriffen wird, um die gewünschte Ausgangsspannung zu erhalten, wobei alternativ zwei Dioden verwendet werden, um den gesamten Zyklus zu gleichrichten, wird als a bezeichnet Center-tapped Full wave rectifier circuit. Der Transformator ist hier im Gegensatz zu den anderen Fällen mittig abgegriffen.

Die Merkmale eines Transformators mit Mittenabgriff sind:

• Das Gewindeschneiden erfolgt durch Ziehen einer Leitung in der Mitte der Sekundärwicklung. Diese Wicklung wird dabei in zwei gleiche Hälften geteilt.

• Die Spannung am abgegriffenen Mittelpunkt ist Null. Dies bildet einen neutralen Punkt.

• Das Mittenabgriff liefert zwei getrennte Ausgangsspannungen, deren Größe gleich ist, deren Polarität jedoch entgegengesetzt ist.

• Eine Anzahl von Tapings kann herausgezogen werden, um unterschiedliche Spannungspegel zu erhalten.

Der Transformator mit Mittenabgriff und zwei Gleichrichterdioden wird beim Aufbau von a verwendet Center-tapped full wave rectifier. Das Schaltbild eines Vollweggleichrichters mit Mittenabgriff ist wie folgt.

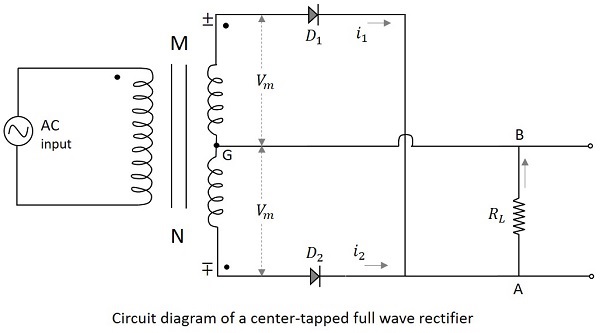
Arbeiten eines CT-FWR

Die Funktionsweise eines Vollweggleichrichters mit Mittenabgriff kann anhand der obigen Abbildung verstanden werden. Wenn die positive Halbwelle der Eingangsspannung angelegt wird, wird der Punkt M an der Transformatorsekundärseite in Bezug auf den Punkt N positiv. Dadurch wird die Diode $ D_1 $ in Vorwärtsrichtung vorgespannt. Daher fließt der Strom $ i_1 $ durch den Lastwiderstand von A nach B. Wir haben jetzt die positiven Halbzyklen im Ausgang

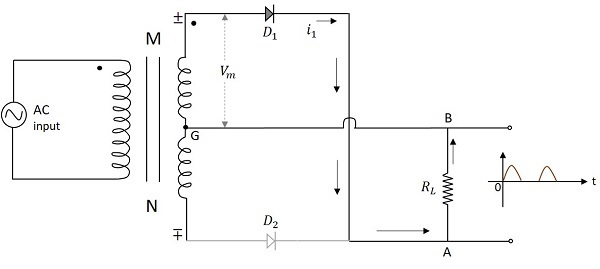
Wenn die negative Halbwelle der Eingangsspannung angelegt wird, wird der Punkt M an der Transformatorsekundärseite in Bezug auf den Punkt N negativ. Dadurch wird die Diode $ D_2 $ in Vorwärtsrichtung vorgespannt. Daher fließt der Strom $ i_2 $ durch den Lastwiderstand von A nach B. Wir haben jetzt die positiven Halbzyklen im Ausgang, selbst während der negativen Halbzyklen des Eingangs.

Wellenformen von CT FWR

Die Eingangs- und Ausgangswellenformen des Vollweggleichrichters mit Mittenabgriff sind wie folgt.

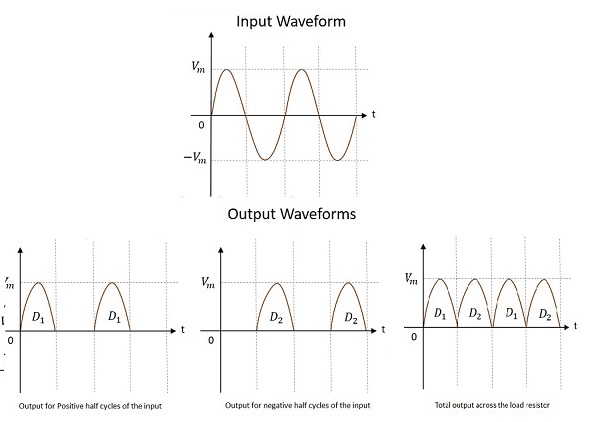
Aus der obigen Figur ist ersichtlich, dass die Ausgabe sowohl für die positiven als auch für die negativen Halbzyklen erhalten wird. Es wird auch beobachtet, dass der Ausgang über dem Lastwiderstand in dersame direction für beide Halbzyklen.

Inverse Spitzenspannung

Da die maximale Spannung an der halben Sekundärwicklung $ V_m $ beträgt, erscheint die gesamte Sekundärspannung an der nichtleitenden Diode. Daher diepeak inverse voltage ist doppelt so hoch wie die maximale Spannung an der Halbleiterwicklung, d. h

$$ PIV = 2V_m $$

Nachteile

Es gibt nur wenige Nachteile für einen Vollweggleichrichter mit Mittenabgriff wie -

• Die Position des Mittelabgriffs ist schwierig
• Die Gleichstromausgangsspannung ist klein
• Der PIV der Dioden sollte hoch sein

Die nächste Art von Vollweggleichrichterschaltung ist die Bridge Full wave rectifier circuit.

Brücken-Vollweggleichrichter

Dies ist eine solche Vollweggleichrichterschaltung, die vier in Brückenform geschaltete Dioden verwendet, um nicht nur den Ausgang während des gesamten Eingangszyklus zu erzeugen, sondern auch um die Nachteile der Mittenabgriff-Vollweggleichrichterschaltung zu beseitigen.

In dieser Schaltung ist kein Mittenabgriff des Transformators erforderlich. Vier Dioden mit den Bezeichnungen $ D_1 $, $ D_2 $, $ D_3 $ und $ D_4 $ werden beim Aufbau eines Brückennetzwerks verwendet, so dass zwei der Dioden für einen halben Zyklus und zwei für den anderen halben Zyklus der Eingangsversorgung leiten. Die Schaltung eines Brückenvollweggleichrichters ist wie in der folgenden Abbildung gezeigt.

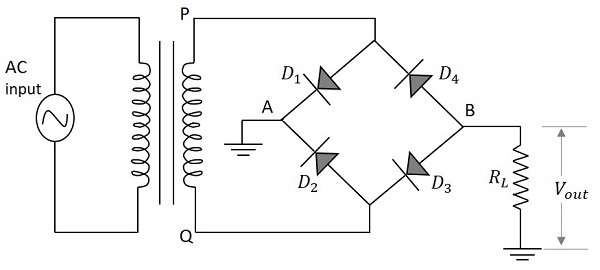
Arbeiten eines Brückengleichrichters

Der Vollweggleichrichter mit vier in der Brückenschaltung angeschlossenen Dioden wird verwendet, um eine bessere Vollwellenausgangsantwort zu erzielen. Wenn die positive Halbwelle der Eingangsversorgung gegeben ist, wird Punkt P in Bezug auf den Punkt positivQ. Dies macht die Diode $ D_1 $ und $ D_3 $ vorwärts vorgespannt, während $ D_2 $ und $ D_4 $ rückwärts vorgespannt sind. Diese beiden Dioden werden nun mit dem Lastwiderstand in Reihe geschaltet.

Die folgende Abbildung zeigt dies zusammen mit dem herkömmlichen Stromfluss in der Schaltung.

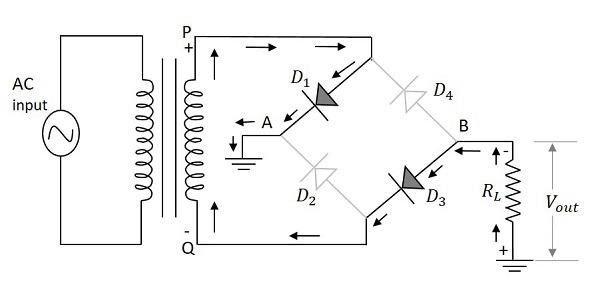
Daher leiten die Dioden $ D_1 $ und $ D_3 $ während der positiven Halbwelle der Eingangsversorgung, um den Ausgang entlang des Lastwiderstands zu erzeugen. Da zwei Dioden arbeiten, um den Ausgang zu erzeugen, ist die Spannung doppelt so hoch wie die Ausgangsspannung des Vollweggleichrichters mit Mittenabgriff.

Wenn die negative Halbwelle der Eingangsversorgung gegeben ist, wird Punkt P in Bezug auf den Punkt negativ Q. Dies macht die Diode $ D_1 $ und $ D_3 $ in Sperrrichtung vorgespannt, während $ D_2 $ und $ D_4 $ in Vorwärtsrichtung vorgespannt sind. Diese beiden Dioden werden nun mit dem Lastwiderstand in Reihe geschaltet.

Die folgende Abbildung zeigt dies zusammen mit dem herkömmlichen Stromfluss in der Schaltung.

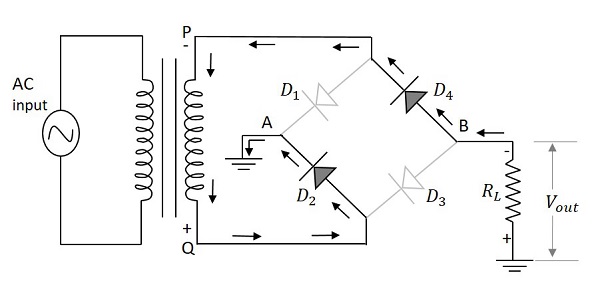
Daher leiten die Dioden $ D_ {2} $ und $ D_ {4} $ während der negativen Halbwelle der Eingangsversorgung, um den Ausgang entlang des Lastwiderstands zu erzeugen. Auch hier erzeugen zwei Dioden die Ausgangsspannung. Der Strom fließt in die gleiche Richtung wie während der positiven Halbwelle des Eingangs.

Wellenformen der Brücke FWR

Die Eingangs- und Ausgangswellenformen des Vollweggleichrichters mit Mittenabgriff sind wie folgt.

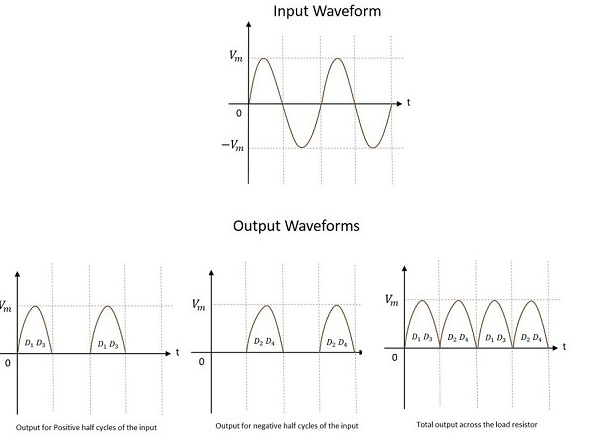
Aus der obigen Figur ist ersichtlich, dass die Ausgabe sowohl für die positiven als auch für die negativen Halbzyklen erhalten wird. Es wird auch beobachtet, dass der Ausgang über dem Lastwiderstand in dersame direction für beide Halbzyklen.

Inverse Spitzenspannung

Immer wenn zwei der Dioden parallel zur Sekundärseite des Transformators sind, erscheint die maximale Sekundärspannung über dem Transformator an den nichtleitenden Dioden, die den PIV der Gleichrichterschaltung bilden. Daher diepeak inverse voltage ist die maximale Spannung über der Sekundärwicklung, dh

$$ PIV = V_m $$

Vorteile

Es gibt viele Vorteile für einen Brücken-Vollweggleichrichter, wie z.

• Keine Notwendigkeit, in die Mitte zu tippen.
• Die Gleichstromausgangsspannung ist doppelt so hoch wie die des Center-Tapper-FWR.
• Der PIV der Dioden hat den halben Wert des Center-Tapper-FWR.
• Das Design der Schaltung ist bei besserer Ausgabe einfacher.

Lassen Sie uns nun die Eigenschaften eines Vollweggleichrichters analysieren.

Analyse des Vollweggleichrichters

Um eine Vollweggleichrichterschaltung zu analysieren, nehmen wir die Eingangsspannung $ V_ {i} $ als an.

$$ V_ {i} = V_m \ sin \ omega t $$

Der Strom $ i_1 $ durch den Lastwiderstand $ R_L $ ist gegeben durch

$$ i_1 = I_m \ sin \ omega t \ quad für \ quad0 \ leq \ omega t \ leq \ pi $$

$$ i_1 = \ quad0 \ quad \ quad \ quad für \ quad \ pi \ leq \ omega t \ leq 2 \ pi $$

Wo

$$ I_m = \ frac {V_m} {R_f + R_L} $$

$ R_f $ ist der Diodenwiderstand im EIN-Zustand.

In ähnlicher Weise ist der Strom $ i_2 $, der durch die Diode $ D_2 $ und den Lastwiderstand RL fließt, gegeben durch:

$$ i_2 = \ quad \: 0 \ quad \ quad \ quad für \ quad 0 \ leq \ omega t \ leq \ pi $$

$$ i_2 = I_m \ sin \ omega t \ quad für \ quad \ pi \ leq \ omega t \ leq 2 \ pi $$

Der durch $ R_L $ fließende Gesamtstrom ist die Summe der beiden Ströme $ i_1 $ und $ i_2 $ dh

$$ i = i_1 + i_2 $$

Gleichstrom oder Durchschnittsstrom

Der Durchschnittswert des Ausgangsstroms, den ein Gleichstrom-Amperemeter anzeigt, ist gegeben durch

$$ I_ {dc} = \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i_1 \: d \ left (\ omega t \ right) + \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i_2 \: d \ left (\ omega t \ right) $$

$$ = \ frac {1} {2 \ pi \ int_ {0} ^ {\ pi}} I_m \ sin \ omega t \: d \ left (\ omega t \ right) + 0 + 0 + $$

$$ \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} I_m \ sin \ omega t \: d \ left (\ omega t \ right) $$

$$ = \ frac {I_m} {\ pi} + \ frac {I_m} {\ pi} = \ frac {2I_m} {\ pi} = 0,636I_m $$

Dies ist doppelt so viel wie ein Halbwellengleichrichter.

DC-Ausgangsspannung

Die Gleichstromausgangsspannung über der Last ist gegeben durch

$$ V_ {dc} = I_ {dc} \ times R_L = \ frac {2I_mR_L} {\ pi} = 0.636I_mR_L $$

Somit ist die Ausgangsgleichspannung doppelt so hoch wie die eines Halbwellengleichrichters.

Effektivstrom

Der Effektivwert des Stroms ist gegeben durch

$$ I_ {rms} = \ left [\ frac {1} {\ pi} \ int_ {0} ^ {\ pi} t ^ 2 \: d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

Da der Strom in beiden Hälften die gleiche Form hat

$$ = \ left [\ frac {I_ {m} ^ {2}} {\ pi} \ int_ {0} ^ {\ pi} \ sin ^ 2 \ omega t \: d \ left (\ omega t \ right ) \ right] ^ {\ frac {1} {2}} $$

$$ = \ frac {I_m} {\ sqrt {2}} $$

Gleichrichtereffizienz

Der Gleichrichterwirkungsgrad ist definiert als

$$ \ eta = \ frac {P_ {dc}} {P_ {ac}} $$

Jetzt,

$$ P_ {dc} = \ left (V_ {dc} \ right) ^ 2 / R_L = \ left (2V_m / \ pi \ right) ^ 2 $$

Und,

$$ P_ {ac} = \ left (V_ {rms} \ right) ^ 2 / R_L = \ left (V_m / \ sqrt {2} \ right) ^ 2 $$

Deshalb,

$$ \ eta = \ frac {P_ {dc}} {P_ {ac}} = \ frac {\ left (2V_m / \ pi \ right) ^ 2} {\ left (V_m / \ sqrt {2} \ right) ^ 2} = \ frac {8} {\ pi ^ 2} $$

$$ = 0,812 = 81,2 \% $$

Der Gleichrichterwirkungsgrad kann wie folgt berechnet werden:

Die Gleichstromausgangsleistung,

$$ P_ {dc} = I_ {dc} ^ {2} R_L = \ frac {4I_ {m} ^ {2}} {\ pi ^ 2} \ times R_L $$

Die Wechselstrom-Eingangsleistung,

$$ P_ {ac} = I_ {rms} ^ {2} \ left (R_f + R_L \ right) = \ frac {I_ {m} ^ {2}} {2} \ left (R_f + R_L \ right) $ $

Deshalb,

$$ \ eta = \ frac {4I_ {m} ^ {2} R_L / \ pi ^ 2} {I_ {m} ^ {2} \ left (R_f + R_L \ right) / 2} = \ frac {8} {\ pi ^ 2} \ frac {R_L} {\ left (R_f + R_L \ right)} $$

$$ = \ frac {0.812} {\ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$

Daher ist die prozentuale Effizienz

$$ = \ frac {0.812} {1+ \ left (R_f + R_L \ right)} $$

$$ = 81,2 \% \ quad if \: R_f = 0 $$

Somit hat ein Vollweggleichrichter einen doppelten Wirkungsgrad als ein Halbwellengleichrichter.

Welligkeitsfaktor

Der Formfaktor der gleichgerichteten Ausgangsspannung eines Vollweggleichrichters ist gegeben durch

$$ F = \ frac {I_ {rms}} {I_ {dc}} = \ frac {I_m / \ sqrt {2}} {2I_m / \ pi} = 1,11 $$

Der Welligkeitsfaktor $ \ gamma $ ist definiert als (unter Verwendung der Wechselstromkreistheorie)

$$ \ gamma = \ left [\ left (\ frac {I_ {rms}} {I_ {dc}} \ right) -1 \ right] ^ {\ frac {1} {2}} = \ left (F ^ 2 -1 \ right) ^ {\ frac {1} {2}} $$

$$ = \ left [\ left (1.11 \ right) ^ 2 -1 \ right] ^ \ frac {1} {2} = 0.48 $$

Dies ist eine große Verbesserung gegenüber dem Welligkeitsfaktor des Halbwellengleichrichters von 1,21

Verordnung

Die Gleichstromausgangsspannung ist gegeben durch

$$ V_ {dc} = \ frac {2I_mR_L} {\ pi} = \ frac {2V_mR_L} {\ pi \ left (R_f + R_L \ right)} $$

$$ = \ frac {2V_m} {\ pi} \ left [1- \ frac {R_f} {R_f + R_L} \ right] = \ frac {2V_m} {\ pi} -I_ {dc} R_f $$

Transformator-Nutzungsfaktor

Die TUF eines Halbwellengleichrichters beträgt 0,287

Es gibt zwei Sekundärwicklungen in einem Gleichrichter mit Mittelabgriff, und daher ist die TUF des Vollwellengleichrichters mit Mittelabgriff gleich

$$ \ left (TUF \ right) _ {avg} = \ frac {P_ {dc}} {VA \: Bewertung \: von \: a \: Transformator} $$

$$ = \ frac {\ left (TUF \ right) _p + \ left (TUF \ right) _s + \ left (TUF \ right) _s} {3} $$

$$ = \ frac {0,812 + 0,287 + 0,287} {3} = 0,693 $$

Halbwellen- oder Vollwellengleichrichter

Nachdem wir alle Werte der verschiedenen Parameter des Vollweggleichrichters durchlaufen haben, versuchen wir einfach, die Merkmale von Halbwellen- und Vollwellengleichrichtern zu vergleichen und gegenüberzustellen.

Bedingungen	Halbwellengleichrichter	Center Tapped FWR	Brücke FWR
Anzahl der Dioden	$ 1 $	$ 2 $	$ 4 $
Transformatorabgriff	$ No $	$ Ja $	$ No $
Inverse Spitzenspannung	$ V_m $	$ 2V_m $	$ V_m $
Maximale Effizienz	$ 40.6 \% $	$ 81,2 \% $	$ 81,2 \% $
Durchschnitt / Gleichstrom	$ I_m / \ pi $	$ 2I_m / \ pi $	$ 2I_m / \ pi $
Gleichspannung	$ V_m / \ pi $	$ 2V_m / \ pi $	$ 2V_m / \ pi $
Effektivstrom	$ I_m / 2 $	$ I_m / \ sqrt {2} $	$ I_m / \ sqrt {2} $
Welligkeitsfaktor	$ 1,21 $	$ 0,48 $	$ 0,48 $
Ausgangsfrequenz	$ f_ {in} $	$ 2f_ {in} $	$ 2f_ {in} $