Sonderfunktionen von LPF und HPF
Tiefpass- und Hochpassfilterschaltungen werden in vielen Anwendungen als Spezialschaltungen verwendet. Tiefpassfilter (LPF) können alsIntegrator, während der Hochpassfilter (HPF) als Differentiator. Diese beiden mathematischen Funktionen sind nur mit diesen Schaltungen möglich, die den Aufwand eines Elektronikingenieurs in vielen Anwendungen verringern.
Tiefpassfilter als Integrator
Bei niedrigen Frequenzen neigt die kapazitive Reaktanz dazu, unendlich zu werden, und bei hohen Frequenzen wird die Reaktanz Null. Daher hat der LPF bei niedrigen Frequenzen einen endlichen Ausgang und bei hohen Frequenzen ist der Ausgang Null, was für eine Integratorschaltung gleich ist. Daher kann gesagt werden, dass ein Tiefpassfilter als arbeitetintegrator.
Damit sich die LPF als Integrator verhält
$$ \ tau \ gg T $$
Wobei $ \ tau = RC $ die Zeitkonstante der Schaltung ist
Dann ist die Spannungsänderung in C sehr klein.
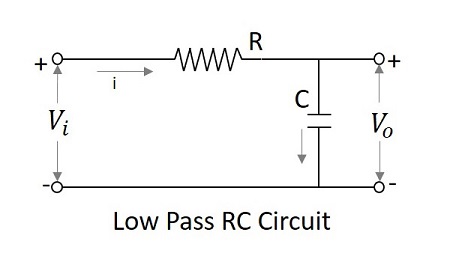
$$ V_ {i} = iR + \ frac {1} {C} \ int i \: dt $$
$$ V_ {i} \ cong iR $$
$$ Seit \: \: \ frac {1} {C} \ int i \: dt \ ll iR $$
$$ i = \ frac {V_ {i}} {R} $$
$$ Seit \: \: V_ {0} = \ frac {1} {C} \ int i dt = \ frac {1} {RC} \ int V_ {i} dt = \ frac {1} {\ tau} \ int V_ {i} dt $$
$$ Output \ propto \ int input $$
Daher erzeugt ein LPF mit großer Zeitkonstante einen Ausgang, der proportional zum Integral eines Eingangs ist.
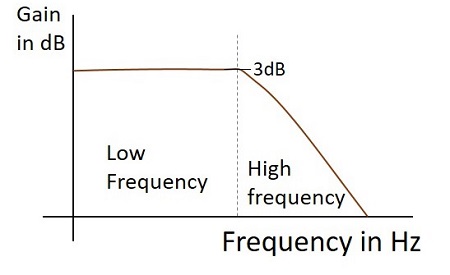
Frequenzgang
Der Frequenzgang eines praktischen Tiefpassfilters, wenn er als Integrator arbeitet, ist wie folgt.
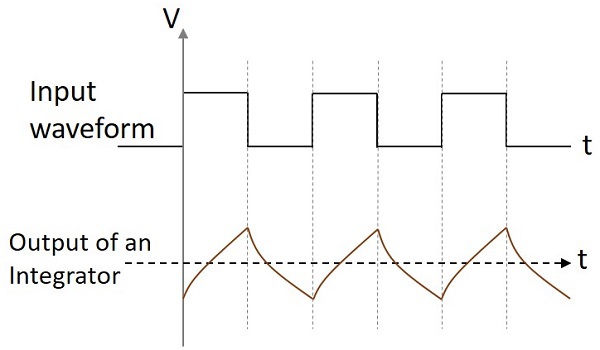
Ausgangswellenform
Wenn die Integratorschaltung einen Sinuswelleneingang erhält, ist der Ausgang eine Cosinuswelle. Wenn der Eingang eine Rechteckwelle ist, ändert die Form der Ausgangswelle ihre Form und erscheint wie in der folgenden Abbildung.
Hochpassfilter als Unterscheidungsmerkmal
Bei niedrigen Frequenzen ist der Ausgang eines Differenzierers Null, während bei hohen Frequenzen sein Ausgang einen endlichen Wert hat. Dies ist das gleiche wie für ein Unterscheidungsmerkmal. Daher soll sich das Hochpassfilter als Unterscheidungsmerkmal verhalten.
Wenn die Zeitkonstante des RC HPF sehr viel kleiner als die Zeitdauer des Eingangssignals ist, verhält sich die Schaltung als Differenzierer. Dann ist der Spannungsabfall über R im Vergleich zum Abfall über C sehr gering.
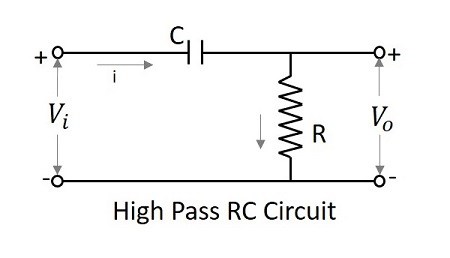
$$ V_ {i} = \ frac {1} {C} \ int i \: dt + iR $$
Aber $ iR = V_ {0} $ ist klein
$$ da V_ {i} = \ frac {1} {C} \ int i \: dt $$
$$ i = \ frac {V_ {0}} {R} $$
$$ Seit \: V_ {i} = \ frac {1} {\ tau} \ int V_ {0} \: dt $$
Wobei $ \ tau = RC $ die Zeitkonstante der Schaltung ist.
Differenzierung auf beiden Seiten,
$$ \ frac {dV_ {i}} {dt} = \ frac {V_0} {\ tau} $$
$$ V_ {0} = \ tau \ frac {dV_ {i}} {dt} $$
$$ Seit \: V_ {0} \ propto \ frac {dV_ {i}} {dt} $$
Der Ausgang ist proportional zur Differenz des Eingangssignals.
Frequenzgang
Der Frequenzgang eines praktischen Hochpassfilters, wenn er als Differenzierer arbeitet, ist wie unten gezeigt.
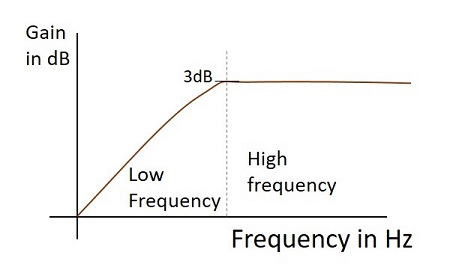
Ausgangswellenform
Wenn die Differenzierschaltung einen Sinuswelleneingang erhält, ist der Ausgang eine Cosinuswelle. Wenn der Eingang eine Rechteckwelle ist, ändert die Form der Ausgangswelle ihre Form und erscheint wie in der folgenden Abbildung.
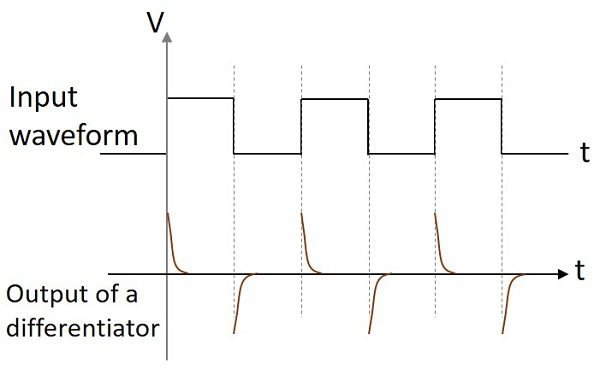
Diese beiden Schaltungen werden hauptsächlich in verschiedenen elektronischen Anwendungen verwendet. Eine Differenzierschaltung erzeugt eine konstante Ausgangsspannung, wenn sich der angelegte Eingang dazu neigt, sich stetig zu ändern. Eine Integratorschaltung erzeugt eine sich stetig ändernde Ausgangsspannung, wenn die angelegte Eingangsspannung konstant ist.