Elektronische Schaltungen - Gleichrichter

Wann immer die Notwendigkeit besteht, einen Wechselstrom in Gleichstrom umzuwandeln, kommt eine Gleichrichterschaltung zur Rettung. Eine einfache PN-Sperrschichtdiode wirkt als Gleichrichter. Die Vorwärtsvorspannungs- und Rückwärtsvorspannungsbedingungen der Diode bewirken die Gleichrichtung.

Berichtigung

Ein Wechselstrom hat die Eigenschaft, seinen Zustand kontinuierlich zu ändern. Dies wird durch Beobachtung der Sinuswelle verstanden, durch die ein Wechselstrom angezeigt wird. Es steigt in seiner positiven Richtung an, geht auf einen positiven Spitzenwert über, reduziert sich von dort auf normal und geht wieder auf den negativen Teil und erreicht den negativen Spitzenwert und kehrt wieder zum Normalwert zurück und geht weiter.

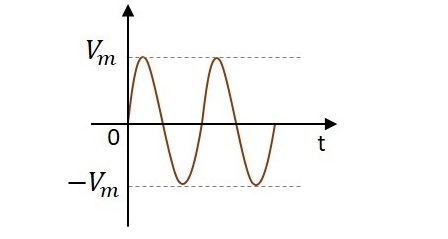
Während ihrer Reise in der Wellenbildung können wir beobachten, dass die Welle in positive und negative Richtungen geht. Eigentlich ändert es sich komplett und daher der Name Wechselstrom.

Während des Gleichrichtungsprozesses wird dieser Wechselstrom jedoch in Gleichstrom umgewandelt. Die Welle, die bis dahin sowohl in positiver als auch in negativer Richtung fließt, wird ihre Richtung nur auf positive Richtung beschränken, wenn sie in Gleichstrom umgewandelt wird. Daher darf der Strom nur in positiver Richtung fließen und widersteht in negativer Richtung, genau wie in der folgenden Abbildung.

Die Schaltung, die die Gleichrichtung durchführt, wird als a bezeichnet Rectifier circuit. Eine Diode wird als Gleichrichter verwendet, um eine Gleichrichterschaltung aufzubauen.

Arten von Gleichrichterschaltungen

Abhängig von ihrer Leistung gibt es zwei Haupttypen von Gleichrichterschaltungen. Sie sind

• Halbwellengleichrichter
• Vollweggleichrichter

Eine Halbwellengleichrichterschaltung korrigiert nur positive Halbzyklen der Eingangsversorgung, während eine Vollwellengleichrichterschaltung sowohl positive als auch negative Halbzyklen der Eingangsversorgung gleichrichtet.

Halbwellengleichrichter

Der Name Halbwellengleichrichter selbst besagt, dass die rectification wird nur für gemacht halfdes Zyklus. Das Wechselstromsignal wird über einen Eingangstransformator abgegeben, der je nach Verwendung nach oben oder unten geht. In Gleichrichterschaltungen wird meist ein Abwärtstransformator verwendet, um die Eingangsspannung zu reduzieren.

Das dem Transformator gegebene Eingangssignal wird durch eine PN-Sperrschichtdiode geleitet, die als Gleichrichter fungiert. Diese Diode wandelt die Wechselspannung nur für die positiven Halbzyklen des Eingangs in pulsierenden Gleichstrom um. Am Ende der Schaltung ist ein Lastwiderstand angeschlossen. Die folgende Abbildung zeigt die Schaltung eines Halbwellengleichrichters.

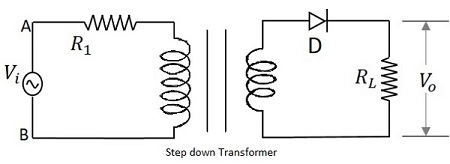
Arbeiten eines HWR

Das Eingangssignal wird an den Transformator gegeben, wodurch die Spannungspegel verringert werden. Der Ausgang des Transformators wird an die Diode abgegeben, die als Gleichrichter fungiert. Diese Diode wird für positive Halbzyklen des Eingangssignals eingeschaltet (leitet). Daher fließt ein Strom in der Schaltung und es tritt ein Spannungsabfall über dem Lastwiderstand auf. Die Diode wird für negative Halbzyklen ausgeschaltet (leitet nicht), und daher ist der Ausgang für negative Halbzyklen $ i_ {D} = 0 $ und $ V_ {o} = 0 $.

Daher ist der Ausgang nur für positive Halbzyklen der Eingangsspannung vorhanden (unter Vernachlässigung des umgekehrten Leckstroms). Dieser Ausgang pulsiert und wird über den Lastwiderstand geleitet.

Wellenformen eines HWR

Die Eingangs- und Ausgangswellenformen sind in der folgenden Abbildung dargestellt.

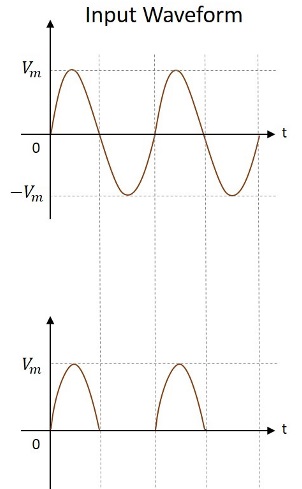
Daher ist der Ausgang eines Halbwellengleichrichters ein pulsierender Gleichstrom. Versuchen wir, die obige Schaltung zu analysieren, indem wir einige Werte verstehen, die vom Ausgang des Halbwellengleichrichters erhalten werden.

Analyse des Halbwellengleichrichters

Um eine Halbwellengleichrichterschaltung zu analysieren, betrachten wir die Gleichung der Eingangsspannung.

$$ v_ {i} = V_ {m} \ sin \ omega t $$

$ V_ {m} $ ist der Maximalwert der Versorgungsspannung.

Nehmen wir an, dass die Diode ideal ist.

• Der Widerstand in Vorwärtsrichtung, dh im EIN-Zustand, beträgt $ R_f $.
• Der Widerstand in umgekehrter Richtung, dh im AUS-Zustand, beträgt $ R_r $.

Die jetzige i in der Diode oder im Lastwiderstand ist $ R_L $ gegeben durch

$ i = I_m \ sin \ omega t \ quad für \ quad 0 \ leq \ omega t \ leq 2 \ pi $

$ i = 0 \ quad \ quad \ quad \ quad für \ quad \ pi \ leq \ omega t \ leq 2 \ pi $

Wo

$$ I_m = \ frac {V_m} {R_f + R_L} $$

DC-Ausgangsstrom

Der durchschnittliche aktuelle $ I_ {dc} $ ist gegeben durch

$$ I_ {dc} = \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i \: d \ left (\ omega t \ right) $$

$$ = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} I_m \ sin \ omega t \: d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0 \: d \ left (\ omega t \ right) \ right] $$

$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {- \ cos \ omega t \ right \} _ {0} ^ {\ pi} \ right] $$

$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {+ 1- \ left (-1 \ right) \ right \} \ right] = \ frac {I_m} {\ pi} = 0,318 I_m $$

Wenn wir den Wert von $ I_m $ einsetzen, erhalten wir

$$ I_ {dc} = \ frac {V_m} {\ pi \ left (R_f + R_L \ right)} $$

Wenn $ R_L >> R_f $, dann

$$ I_ {dc} = \ frac {V_m} {\ pi R_L} = 0,318 \ frac {V_m} {R_L} $$

DC-Ausgangsspannung

Die DC-Ausgangsspannung ist gegeben durch

$$ V_ {dc} = I_ {dc} \ mal R_L = \ frac {I_m} {\ pi} \ mal R_L $$

$$ = \ frac {V_m \ mal R_L} {\ pi \ left (R_f + R_L \ right)} = \ frac {V_m} {\ pi \ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$

Wenn $ R_L >> R_f $, dann

$$ V_ {dc} = \ frac {V_m} {\ pi} = 0,318 V_m $$

Effektivstrom und Spannung

Der Wert des Effektivstroms ist gegeben durch

$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i ^ {2} d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} I_ {m} ^ {2} \ sin ^ {2} \ omega t \: d \ left (\ omega t \ right) + \ frac {1} {2 \ pi} \ int _ {\ pi} ^ {2 \ pi} 0 \: d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {2 \ pi} \ int_ {0} ^ {\ pi} \ left (\ frac {1- \ cos 2 \ omega t} {2 } \ right) d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ left (\ omega t \ right) - \ frac {\ sin 2 \ omega t} {2} \ right \} _ {0} ^ {\ pi} \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ pi - 0 - \ frac {\ sin 2 \ pi} {2} + \ sin 0 \ right \} \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ right] ^ {\ frac {1} {2}} = \ frac {I_m} {2} $$

$$ = \ frac {V_m} {2 \ left (R_f + R_L \ right)} $$

Die Effektivspannung über der Last beträgt

$$ V_ {rms} = I_ {rms} \ mal R_L = \ frac {V_m \ mal R_L} {2 \ links (R_f + R_L \ rechts)} $$

$$ = \ frac {V_m} {2 \ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$

Wenn $ R_L >> R_f $, dann

$$ V_ {rms} = \ frac {V_m} {2} $$

Gleichrichtereffizienz

Jede Schaltung muss effizient arbeiten, um eine bessere Ausgabe zu erzielen. Um den Wirkungsgrad eines Halbwellengleichrichters zu berechnen, muss das Verhältnis der Ausgangsleistung zur Eingangsleistung berücksichtigt werden.

Der Gleichrichterwirkungsgrad ist definiert als

$$ \ eta = \ frac {dcpower \: \: geliefert \: \: an \: \: the \: \: load} {acinput \: \: power \: \: from \: \: transformator \: \ : sekundär} = \ frac {P_ {ac}} {P_ {dc}} $$

Jetzt

$$ P_ {dc} = \ left ({I_ {dc}} \ right) ^ 2 \ times R_L = \ frac {I_m R_L} {\ pi ^ 2} $$

Des Weiteren

$$ P_ {ac} = P_a + P_r $$

Wo

$ P_a = Leistung \: Verlustleistung \: am \: Übergang \: der \: Diode $

$$ = I_ {rms} ^ {2} \ mal R_f = \ frac {I_ {m} ^ {2}} {4} \ mal R_f $$

Und

$$ P_r = Leistung \: zerstreut \: in \: die \: Last \: Widerstand $$

$$ = I_ {rms} ^ {2} \ mal R_L = \ frac {I_ {m} ^ {2}} {4} \ mal R_L $$

$$ P_ {ac} = \ frac {I_ {m} ^ {2}} {4} \ mal R_f + \ frac {I_ {m} ^ {2}} {4} \ mal R_L = \ frac {I_ {m } ^ {2}} {4} \ left (R_f + R_L \ right) $$

Aus den beiden Ausdrücken von $ P_ {ac} $ und $ P_ {dc} $ können wir schreiben

$$ \ eta = \ frac {I_ {m} ^ {2} R_L / \ pi ^ 2} {I_ {m} ^ {2} \ left (R_f + R_L \ right) / 4} = \ frac {4} {\ pi ^ 2} \ frac {R_L} {\ left (R_f + R_L \ right)} $$

$$ = \ frac {4} {\ pi ^ 2} \ frac {1} {\ left \ {1+ \ left (R_f / R_L \ right) \ right \}} = \ frac {0.406} {\ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$

Prozentualer Wirkungsgrad des Gleichrichters

$$ \ eta = \ frac {40.6} {\ lbrace1 + \ lgroup \: R_ {f} / R_ {L} \ rgroup \ rbrace} $$

Theoretisch beträgt der Maximalwert der Gleichrichtereffizienz eines Halbwellengleichrichters 40,6%, wenn $ R_ {f} / R_ {L} = 0 $

Ferner kann der Wirkungsgrad auf folgende Weise berechnet werden

$$ \ eta = \ frac {P_ {dc}} {P_ {ac}} = \ frac {\ left (I_ {dc} \ right) ^ 2R_L} {\ left (I_ {rms} \ right) ^ 2R_L} = \ frac {\ left (V_ {dc} / R_L \ right) ^ 2R_L} {\ left (V_ {rms} / R_L \ right) ^ 2R_L} = \ frac {\ left (V_ {dc} \ right) ^ 2} {\ left (V_ {rms} \ right) ^ 2} $$

$$ = \ frac {\ left (V_m / \ pi \ right) ^ 2} {\ left (V_m / 2 \ right) ^ 2} = \ frac {4} {\ pi ^ 2} = 0,406 $$

$$ = 40,6 \% $$

Welligkeitsfaktor

Der gleichgerichtete Ausgang enthält eine gewisse Menge an Wechselstromkomponente in Form von Welligkeiten. Dies wird unter Beobachtung der Ausgangswellenform des Halbwellengleichrichters verstanden. Um einen reinen Gleichstrom zu erhalten, müssen wir eine Idee zu dieser Komponente haben.

Der Welligkeitsfaktor gibt die Welligkeit des gleichgerichteten Ausgangs an. Es wird mit bezeichnety. Dies kann als das Verhältnis des effektiven Wertes der Wechselstromkomponente von Spannung oder Strom zum direkten Wert oder Durchschnittswert definiert werden.

$$ \ gamma = \ frac {Welligkeit \: Spannung} {Gleichstrom \: Spannung} = \ frac {Effektivwert \: Wert \: von \: Begleiter} {Gleichstrom \: von \: Welle} = \ frac {\ left ( V_r \ right) _ {rms}} {v_ {dc}} $$

Hier,

$$ \ left (V_r \ right) _ {rms} = \ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}} $$

Deshalb,

$$ \ gamma = \ frac {\ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}}} {V_ {dc}} = \ sqrt {\ left (\ frac {V_ {rms} } {V_ {dc}} \ right) ^ 2-1} $$

Jetzt,

$$ V_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} V_ {m} ^ {2} \ sin ^ 2 \ omega t \: d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ = V_m \ left [\ frac {1} {4 \ pi} \ int_ {0} ^ {\ pi} \ left (1- \ cos2 \: \ omega t \ right) d \ left (\ omega t \ rechts) \ rechts] ^ {\ frac {1} {2}} = \ frac {V_m} {2} $$

$$ V_ {dc} = V_ {av} = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} V_m \ sin \ omega t \: d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0.d \ left (\ omega t \ right) \ right] $$

$$ = \ frac {V_m} {2 \ pi} \ left [- \ cos \ omega t \ right] _ {0} ^ {\ pi} = \ frac {V_m} {\ pi} $$

$$ \ gamma = \ sqrt {\ left [\ left \ {\ frac {\ left (V_m / 2 \ right)} {\ left (V_m / \ pi \ right)} \ right \} ^ 2-1 \ right ]} = \ sqrt {\ left \ {\ left (\ frac {\ pi} {2} \ right) ^ 2-1 \ right \}} = 1,21 $$

Der Welligkeitsfaktor ist auch definiert als

$$ \ gamma = \ frac {\ left (I_r \ right) _ {rms}} {I_ {dc}} $$

Da der Wert des in einem Halbwellengleichrichter vorhandenen Welligkeitsfaktors 1,21 beträgt, bedeutet dies, dass die im Ausgang vorhandene Wechselstrommenge $ 121 \% $ der Gleichspannung beträgt

Verordnung

Der Strom durch die Last kann je nach Lastwiderstand variieren. Aber selbst unter solchen Bedingungen erwarten wir, dass unsere Ausgangsspannung, die über diesen Lastwiderstand angelegt wird, konstant ist. Daher muss unsere Spannung auch unter verschiedenen Lastbedingungen geregelt werden.

Die Änderung der DC-Ausgangsspannung mit Änderung des DC-Laststroms ist definiert als Regulation. Die prozentuale Regulierung wird wie folgt berechnet.

$$ Prozentsatz \: Regulation = \ frac {V_ {no \: load} -V_ {full \: load}} {V_ {full \: load}} \ times 100 \% $$

Je niedriger die prozentuale Regelung ist, desto besser wäre die Stromversorgung. Ein ideales Netzteil hat eine Null-Prozent-Regelung.

Transformator-Nutzungsfaktor

Die Gleichstromleistung, die in einem Gleichrichterschaltkreis an die Last geliefert werden soll, bestimmt die Nennleistung des in einem Stromkreis verwendeten Transformators.

Der Transformatorauslastungsfaktor ist also definiert als

$$ TUF = \ frac {dcpower \: to \: be \: geliefert \: to \: the \: load} {acrating \: of \: the \: transformator \: sekundär} $$

$$ = \ frac {P_ {dc}} {P_ {ac \ left (bewertet \ right)}} $$

Nach der Theorie des Transformators beträgt die Nennspannung der Sekundärseite

$$ V_m / \ sqrt {2} $$

Die tatsächlich durchfließende Effektivspannung beträgt

$$ I_m / 2 $$

Deshalb

$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left (V_m / \ sqrt {2} \ right) \ times \ left (I_m / 2 \ right)} $ $

Aber

$$ V_m = I_m \ left (R_f + R_L \ right) $$

Deshalb

$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left \ {I_m \ left (R_f + R_L \ right) / \ sqrt {2} \ right \} \ times \ left (I_m / 2 \ right)} $$

$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} \ times \ frac {R_L} {\ left (R_f + R_L \ right)} $$

$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} = 0,287 $$

Inverse Spitzenspannung

Eine Diode sollte, wenn sie in Sperrrichtung angeschlossen ist, unter einem kontrollierten Spannungspegel betrieben werden. Wenn diese sichere Spannung überschritten wird, wird die Diode beschädigt. Daher ist es sehr wichtig, über diese maximale Spannung Bescheid zu wissen.

Die maximale inverse Spannung, der die Diode standhalten kann, ohne zerstört zu werden, wird als bezeichnet Peak Inverse Voltage. Zusamenfassend,PIV.

Hier ist der PIV nichts als Vm

Formfaktor

Dies kann als mathematisches Mittel der Absolutwerte aller Punkte auf der Wellenform verstanden werden. Dasform factorist definiert als das Verhältnis des Effektivwerts zum Durchschnittswert. Es wird mit bezeichnetF.

$$ F = \ frac {rms \: Wert} {Durchschnitt \: Wert} = \ frac {I_m / 2} {I_m / \ pi} = \ frac {0,5I_m} {0,318I_m} = 1,57 $$

Spitzenfaktor

Der Wert der Spitze in der Welligkeit muss berücksichtigt werden, um zu wissen, wie effektiv die Gleichrichtung ist. Der Wert des Spitzenfaktors ist ebenfalls ein wichtiger Gesichtspunkt.Peak factor ist definiert als das Verhältnis des Spitzenwerts zum Effektivwert.

Deshalb

$$ Peak Factor = \ frac {Peak \: Wert} {rms \: Wert} = \ frac {V_m} {V_m / 2} = 2 $$

All dies sind die wichtigen Parameter, die beim Studium eines Gleichrichters berücksichtigt werden müssen.