Mikrowellentechnik - E-Plane Tee

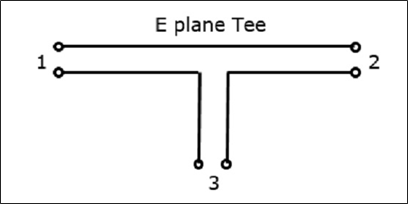
Ein E-Plane-Tee-Übergang wird gebildet, indem ein einfacher Wellenleiter an der breiteren Abmessung eines rechteckigen Wellenleiters angebracht wird, der bereits zwei Anschlüsse hat. Die Arme rechteckiger Wellenleiter bilden zwei Portscollinear ports dh Port1 und Port2, während der neue Port3 als Seitenarm oder bezeichnet wird E-arm. Dieses E-Flugzeug Tee wird auch als bezeichnetSeries Tee.

Da die Achse des Seitenarms parallel zum elektrischen Feld ist, wird diese Verbindung als E-Plane Tee-Verbindung bezeichnet. Dies wird auch als bezeichnetVoltage oder Series junction. Die Anschlüsse 1 und 2 sind um 180 ° zueinander phasenverschoben. Die Querschnittsdetails des T-Stücks in der E-Ebene können aus der folgenden Abbildung verstanden werden.

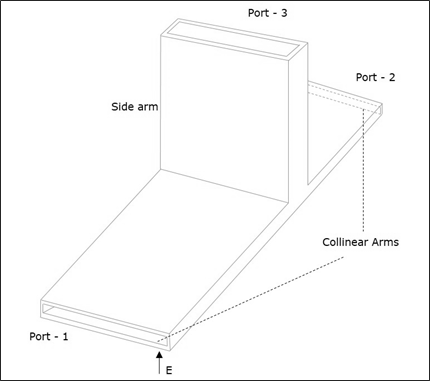
Die folgende Abbildung zeigt die Verbindung der Seitenwaffe mit dem bidirektionalen Wellenleiter zur Bildung des parallelen Anschlusses.

Eigenschaften des E-Flugzeug-T-Stücks

Die Eigenschaften von E-Plane Tee können durch seine $ [S] _ {3x3} $ -Matrix definiert werden.

Es ist eine 3 × 3-Matrix, da es 3 mögliche Eingänge und 3 mögliche Ausgänge gibt.

$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {21} & S_ {22} & S_ {23} \\ S_ {31} & S_ {32 } & S_ {33} \ end {bmatrix} $ ........ Equation 1

Die Streukoeffizienten $ S_ {13} $ und $ S_ {23} $ sind mit einem Eingang an Port 3 um 180 ° phasenverschoben.

$ S_ {23} = -S_ {13} $........ Equation 2

Der Hafen ist perfekt auf die Kreuzung abgestimmt.

$ S_ {33} = 0 $........ Equation 3

Aus der symmetrischen Eigenschaft,

$ S_ {ij} = S_ {ji} $

$ S_ {12} = S_ {21} \: \: S_ {23} = S_ {32} \: \: S_ {13} = S_ {31} $........ Equation 4

Unter Berücksichtigung der Gleichungen 3 und 4 kann die $ [S] $ -Matrix wie folgt geschrieben werden:

$ [S] = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} $........ Equation 5

Wir können sagen, dass wir vier Unbekannte haben, wenn man die Symmetrieeigenschaft berücksichtigt.

Aus dem Unitary-Eigentum

$$ [S] [S] \ ast = [I] $$

$$ \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13} \\ S_ {12} & S_ {22} & -S_ {13} \\ S_ {13} & -S_ {13} & 0 \ end {bmatrix} \: \ begin {bmatrix} S_ {11} ^ {*} & S_ {12} ^ {*} & S_ {13} ^ {*} \\ S_ {12} ^ {*} & S_ {22} ^ {*} & -S_ {13} ^ {*} \\ S_ {13} ^ {*} & -S_ {13} ^ {*} & 0 \ end {bmatrix} = \ begin { bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} $$

Multiplikation bekommen wir,

(R als Zeile und C als Spalte notieren)

$ R_1C_1: S_ {11} S_ {11} ^ {*} + S_ {12} S_ {12} ^ {*} + S_ {13} S_ {13} ^ {*} = 1 $

$ \ left | S_ {11} \ rechts | ^ 2 + \ links | S_ {11} \ rechts | ^ 2 + \ links | S_ {11} \ right | ^ 2 = 1 $........ Equation 6

$ R_2C_2: \ left | S_ {12} \ right | ^ 2 + \ left | S_ {22} \ right | ^ 2 + \ left | S_ {13} \ right | ^ 2 = 1 $......... Equation 7

$ R_3C_3: \ left | S_ {13} \ rechts | ^ 2 + \ links | S_ {13} \ right | ^ 2 = 1 $......... Equation 8

$ R_3C_1: S_ {13} S_ {11} ^ {*} - S_ {13} S_ {12} ^ {*} = 1 $ ......... Equation 9

Wenn wir die Gleichungen 6 und 7 gleichsetzen, erhalten wir

$ S_ {11} = S_ {22} $ ......... Equation 10

Aus Gleichung 8,

$ 2 \ left | S_ {13} \ right | ^ 2 \ quad oder \ quad S_ {13} = \ frac {1} {\ sqrt {2}} $......... Equation 11

Aus Gleichung 9,

$ S_ {13} \ left (S_ {11} ^ {*} - S_ {12} ^ {*} \ right) $

Oder $ S_ {11} = S_ {12} = S_ {22} $ ......... Equation 12

Unter Verwendung der Gleichungen 10, 11 und 12 in der Gleichung 6,

wir bekommen,

$ \ left | S_ {11} \ rechts | ^ 2 + \ links | S_ {11} \ right | ^ 2 + \ frac {1} {2} = 1 $

$ 2 \ left | S_ {11} \ right | ^ 2 = \ frac {1} {2} $

Oder $ S_ {11} = \ frac {1} {2} $ ......... Equation 13

Einsetzen der Werte aus den obigen Gleichungen in die $ [S] $ -Matrix,

Wir bekommen,

$$ \ left [S \ right] = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac { 1} {2} & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2}} & - \ frac {1} { \ sqrt {2}} & 0 \ end {bmatrix} $$

Wir wissen, dass $ [b] $ = $ [S] [a] $

$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \ end {bmatrix} = \ begin {bmatrix} \ frac {1} {2} & \ frac {1} {2} & \ frac {1} {\ sqrt {2}} \\ \ frac {1} {2} & \ frac {1} {2} & - \ frac {1} {\ sqrt {2}} \\ \ frac {1} {\ sqrt {2 }} & - \ frac {1} {\ sqrt {2}} & 0 \ end {bmatrix} \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \ end {bmatrix} $$

Dies ist die Streumatrix für E-Plane Tee, die die Streueigenschaften erklärt.