Mikrowellentechnik - Mikrowellengeräte

Wie andere Systeme bestehen auch die Mikrowellensysteme aus vielen Mikrowellenkomponenten, hauptsächlich mit Quelle an einem Ende und Last am anderen, die alle mit Wellenleitern oder Koaxialkabel- oder Übertragungsleitungssystemen verbunden sind.

Es folgen die Eigenschaften von Wellenleitern.

Hohes SNR
Geringe Dämpfung
Geringerer Einfügungsverlust

Wellenleiter-Mikrowellenfunktionen

Stellen Sie sich einen Wellenleiter mit 4 Ports vor. Wenn die Stromversorgung an einen Port angelegt wird, werden alle drei Ports in bestimmten Anteilen durchlaufen, wobei ein Teil davon möglicherweise vom selben Port zurückgespiegelt wird. Dieses Konzept ist in der folgenden Abbildung deutlich dargestellt.

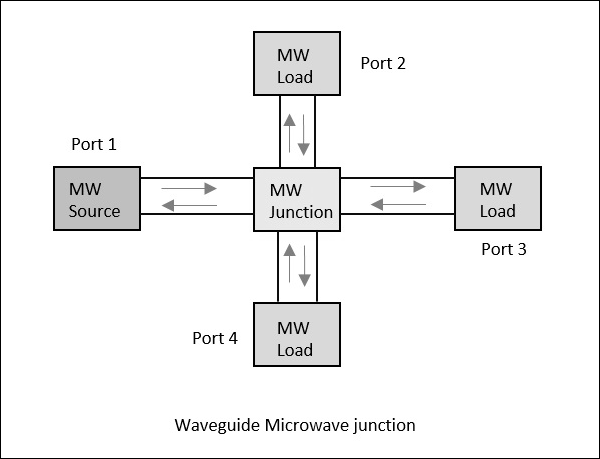
Streuparameter

Wenn in einem Netzwerk mit zwei Ports, wie in der folgenden Abbildung gezeigt, der Strom an einem Port angelegt wird, wie wir gerade besprochen haben, entweicht der größte Teil des Stroms vom anderen Port, während ein Teil davon auf denselben Port zurückgeführt wird. In der folgenden Abbildung, wennV₁ oder V₂ wird dann angewendet I₁ oder I₂ Strom fließt jeweils.

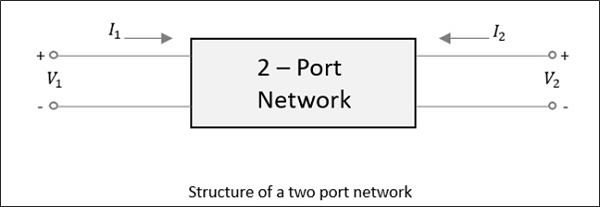
Wenn die Quelle auf den gegenüberliegenden Port angewendet wird, sind zwei weitere Kombinationen zu berücksichtigen. Für ein Netzwerk mit zwei Ports treten wahrscheinlich 2 × 2 = 4 Kombinationen auf.

Die Wanderwellen mit zugehörigen Leistungen bei Streuung durch die Ports, den Mikrowellenübergang können durch S-Parameter oder definiert werden Scattering Parameters, die in einer Matrixform dargestellt werden, genannt als "Scattering Matrix".

Streumatrix

Es ist eine quadratische Matrix, die alle Kombinationen von Leistungsbeziehungen zwischen den verschiedenen Eingangs- und Ausgangsanschlüssen eines Mikrowellenübergangs angibt. Die Elemente dieser Matrix werden aufgerufen"Scattering Coefficients" oder "Scattering (S) Parameters".

Betrachten Sie die folgende Abbildung.

Hier ist die Quelle über die Linie $ i ^ {th} $ verbunden, während $ a_1 $ die einfallende Welle und $ b_1 $ die reflektierte Welle ist.

Wenn eine Beziehung zwischen $ b_1 $ und $ a_1 $ gegeben ist,

$$ b_1 = (Reflexion \: \: Koeffizient) a_1 = S_ {1i} a_1 $$

$ S_ {1i} $ = Reflexionskoeffizient der Linie $ 1 ^ {st} $ (wobei $ i $ der Eingabeport und $ 1 $ der Ausgabeport ist)
$ 1 $ = Reflexion von $ 1 ^ {st} $ line
$ i $ = Quelle verbunden in der Zeile $ i ^ {th} $

Wenn die Impedanz übereinstimmt, wird die Leistung auf die Last übertragen. Unwahrscheinlich, wenn die Lastimpedanz nicht mit der charakteristischen Impedanz übereinstimmt. Dann tritt die Reflexion auf. Das heißt, Reflexion tritt auf, wenn

$$ Z_l \ neq Z_o $$

Wenn diese Nichtübereinstimmung jedoch für mehr als einen Port vorliegt, z. B. $ 'n' $ Ports, dann ist $ i = 1 $ bis $ n $ (da $ i $ eine beliebige Zeile von $ 1 $ bis $ n $ sein kann).

Deshalb haben wir

$$ b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n $$

$$ b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n $$

$$. $$

$$ b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n $$

Wenn das Ganze in einer Matrixform gehalten wird,

$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \\. \\. \\. \\ b_n \ end {bmatrix} = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13 } & ... & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & ... & S_ {2n} \\. &. &. & ... &. \\. &. &. & ... &. \\. &. &. & ... &. \\ S_ {n1} & S_ {n2} & S_ {n3} & ... & S_ {nn} \\ \ end {bmatrix} \ times \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \\. \ \. \\. \\ a_n \ end {bmatrix} $$

Column matrix $ [b] $ Scattering matrix $ [S] $Matrix $ [a] $

Die Spaltenmatrix $ \ left [b \ right] $ entspricht den reflektierten Wellen oder der Ausgabe, während die Matrix $ \ left [a \ right] $ den einfallenden Wellen oder der Eingabe entspricht. Die Streusäulenmatrix $ \ left [s \ right] $, die in der Größenordnung von $ n \ times n $ liegt, enthält die Reflexionskoeffizienten und Transmissionskoeffizienten. Deshalb,

$$ \ left [b \ right] = \ left [S \ right] \ left [a \ right] $$

Eigenschaften der [S] Matrix

Die Streumatrix wird als $ [S] $ -Matrix angegeben. Es gibt nur wenige Standardeigenschaften für die $ [S] $ -Matrix. Sie sind -

$ [S] $ ist immer eine quadratische Ordnungsmatrix (nxn)

$ [S] _ {n \ times n} $
$ [S] $ ist eine symmetrische Matrix

dh $ S_ {ij} = S_ {ji} $
$ [S] $ ist eine einheitliche Matrix

dh $ [S] [S] ^ * = I $
Die Summe der Produkte jedes Terms einer Zeile oder Spalte multipliziert mit dem komplexen Konjugat der entsprechenden Terme einer anderen Zeile oder Spalte ist Null. dh

$$ \ sum_ {i = j} ^ {n} S_ {ik} S_ {ik} ^ {*} = 0 \: für \: k \ neq j $$

$$ (k = 1,2,3, ... \: n) \: und \: (j = 1,2,3, ... \: n) $$

Wenn der elektrische Abstand zwischen einem $ k ^ {th} $ -Port und der Verbindungsstelle $ \ beta _kI_k $ ist, werden die Koeffizienten von $ S_ {ij} $, an denen $ k $ beteiligt ist, mit dem Faktor $ e ^ {- multipliziert j \ beta kIk} $

In den nächsten Kapiteln werden wir uns verschiedene Arten von Mikrowellen-T-Übergängen ansehen.