Diskrete Systemsimulation
In diskreten Systemen sind die Änderungen des Systemzustands diskontinuierlich und jede Änderung des Systemzustands wird als bezeichnet event. Das in einer diskreten Systemsimulation verwendete Modell verfügt über eine Reihe von Zahlen zur Darstellung des Systemzustands, die als a bezeichnet werdenstate descriptor. In diesem Kapitel lernen wir auch die Warteschlangensimulation kennen, die neben der Simulation eines Time-Sharing-Systems ein sehr wichtiger Aspekt bei der diskreten Ereignissimulation ist.
Es folgt die grafische Darstellung des Verhaltens einer diskreten Systemsimulation.
Diskrete Ereignissimulation ─ Hauptmerkmale
Die diskrete Ereignissimulation wird im Allgemeinen von einer Software ausgeführt, die in höheren Programmiersprachen wie Pascal, C ++ oder einer beliebigen speziellen Simulationssprache entwickelt wurde. Im Folgenden sind die fünf Hauptmerkmale aufgeführt:
Entities - Dies sind die Darstellungen realer Elemente wie Maschinenteile.
Relationships - Es bedeutet, Entitäten miteinander zu verbinden.
Simulation Executive - Es ist verantwortlich für die Steuerung der Vorlaufzeit und die Ausführung diskreter Ereignisse.
Random Number Generator - Es hilft, verschiedene Daten zu simulieren, die in das Simulationsmodell eingehen.
Results & Statistics - Es validiert das Modell und liefert seine Leistungsmessungen.
Zeitdiagrammdarstellung
Jedes System hängt von einem Zeitparameter ab. In einer grafischen Darstellung wird es als Uhrzeit oder Zeitzähler bezeichnet und zunächst auf Null gesetzt. Die Zeit wird basierend auf den folgenden zwei Faktoren aktualisiert:
Time Slicing - Dies ist die von einem Modell für jedes Ereignis festgelegte Zeit bis zum Fehlen eines Ereignisses.
Next Event- Dies ist das vom Modell definierte Ereignis für das nächste auszuführende Ereignis anstelle eines Zeitintervalls. Es ist effizienter als Time Slicing.
Simulation eines Warteschlangensystems
Eine Warteschlange ist die Kombination aller Entitäten im System, die bedient werden, und derjenigen, die darauf warten, dass sie an die Reihe kommen.
Parameter
Im Folgenden finden Sie eine Liste der im Warteschlangensystem verwendeten Parameter.
| Symbol | Beschreibung |
|---|---|
| λ | Bezeichnet die Ankunftsrate, dh die Anzahl der Ankünfte pro Sekunde |
| Ts | Bezeichnet die mittlere Servicezeit für jede Ankunft ohne die Wartezeit in der Warteschlange |
| σTs | Bezeichnet die Standardabweichung der Servicezeit |
| ρ | Bezeichnet die Serverauslastung, sowohl im Leerlauf als auch im ausgelasteten Zustand |
| u | Bezeichnet die Verkehrsintensität |
| r | Bezeichnet den Mittelwert der Elemente im System |
| R. | Bezeichnet die Gesamtzahl der Elemente im System |
| Tr | Bezeichnet die mittlere Zeit eines Elements im System |
| TR | Bezeichnet die Gesamtzeit eines Elements im System |
| σr | Bezeichnet die Standardabweichung von r |
| σTr | Bezeichnet die Standardabweichung von Tr |
| w | Bezeichnet die durchschnittliche Anzahl der in der Warteschlange wartenden Elemente |
| σw | Bezeichnet die Standardabweichung von w |
| Tw | Bezeichnet die mittlere Wartezeit aller Artikel |
| Td | Bezeichnet die mittlere Wartezeit der in der Warteschlange wartenden Elemente |
| N. | Bezeichnet die Anzahl der Server in einem System |
| mx (y) | Bezeichnet das y- te Perzentil, was den Wert von y bedeutet, unter dem x y Prozent der Zeit auftritt |
Single Server Queue
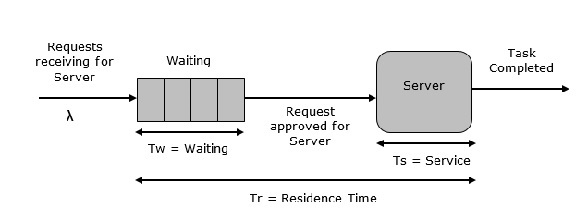
Dies ist das einfachste Warteschlangensystem, wie in der folgenden Abbildung dargestellt. Das zentrale Element des Systems ist ein Server, der die verbundenen Geräte oder Elemente bedient. Elemente fordern das zu bedienende System an, wenn der Server inaktiv ist. Dann wird es sofort zugestellt, andernfalls tritt es in eine Warteschlange ein. Nachdem die Aufgabe vom Server abgeschlossen wurde, wird der Artikel verlassen.
Multi Server Queue
Wie der Name schon sagt, besteht das System aus mehreren Servern und einer gemeinsamen Warteschlange für alle Elemente. Wenn ein Element für den Server angefordert wird, wird es zugewiesen, wenn mindestens ein Server verfügbar ist. Andernfalls beginnt die Warteschlange zu starten, bis der Server frei ist. In diesem System gehen wir davon aus, dass alle Server identisch sind, dh es gibt keinen Unterschied, welcher Server für welches Element ausgewählt wird.
Es gibt eine Ausnahme der Nutzung. LassenN seien Sie also die identischen Server ρist die Auslastung jedes Servers. ErwägenNρdie Nutzung des gesamten Systems zu sein; dann ist die maximale AuslastungN*100%und die maximale Eingaberate ist -
$ λmax = \ frac {\ text {N}} {\ text {T} s} $

Warteschlangenbeziehungen
Die folgende Tabelle zeigt einige grundlegende Warteschlangenbeziehungen.
| Allgemeine Geschäftsbedingungen | Einzelner Server | Multi Server |
|---|---|---|
| r = λTr Little's Formel | ρ = λTs | ρ = λTs / N. |
| w = λTw Little Formel | r = w + ρ | u = λTs = ρN |
| Tr = Tw + Ts | r = w + Nρ |
Simulation eines Time-Sharing-Systems
Das Time-Sharing-System ist so konzipiert, dass jeder Benutzer einen kleinen Teil der auf einem System gemeinsam genutzten Zeit verwendet, was dazu führt, dass mehrere Benutzer das System gleichzeitig gemeinsam nutzen. Der Wechsel jedes Benutzers erfolgt so schnell, dass jeder Benutzer das Gefühl hat, sein eigenes System zu verwenden. Es basiert auf dem Konzept der CPU-Planung und der Mehrfachprogrammierung, bei dem mehrere Ressourcen effektiv genutzt werden können, indem mehrere Jobs gleichzeitig auf einem System ausgeführt werden.
Example - SimOS Simulationssystem.
Es wurde von der Stanford University entwickelt, um die komplexen Computerhardware-Designs zu untersuchen, die Anwendungsleistung zu analysieren und die Betriebssysteme zu untersuchen. SimOS enthält eine Software-Simulation aller Hardwarekomponenten moderner Computersysteme, dh Prozessoren, Speicherverwaltungseinheiten (MMU), Caches usw.