Modellierung & Simulation - Kurzanleitung

Modellingist der Prozess der Darstellung eines Modells, das dessen Konstruktion und Arbeitsweise umfasst. Dieses Modell ähnelt einem realen System, mit dessen Hilfe der Analyst die Auswirkungen von Änderungen am System vorhersagen kann. Mit anderen Worten, beim Modellieren wird ein Modell erstellt, das ein System mit seinen Eigenschaften darstellt. Es ist ein Akt des Modellbaus.

Simulationeines Systems ist der zeitliche oder räumliche Betrieb eines Modells, mit dessen Hilfe die Leistung eines vorhandenen oder eines vorgeschlagenen Systems analysiert werden kann. Mit anderen Worten, Simulation ist der Prozess der Verwendung eines Modells zur Untersuchung der Leistung eines Systems. Es ist ein Akt der Verwendung eines Modells für die Simulation.

Geschichte der Simulation

Die historische Perspektive der Simulation ist in chronologischer Reihenfolge aufgezählt.

1940 - Eine Methode namens "Monte Carlo" wurde von Forschern (John von Neumann, Stanislaw Ulan, Edward Teller, Herman Kahn) und Physikern entwickelt, die an einem Manhattan-Projekt zur Untersuchung der Neutronenstreuung arbeiteten.
1960 - Die ersten speziellen Simulationssprachen wurden entwickelt, wie beispielsweise SIMSCRIPT von Harry Markowitz von der RAND Corporation.
1970 - In dieser Zeit wurden Untersuchungen zu mathematischen Grundlagen der Simulation eingeleitet.
1980 - In dieser Zeit wurden PC-basierte Simulationssoftware, grafische Benutzeroberflächen und objektorientierte Programmierung entwickelt.
1990 - In dieser Zeit wurden webbasierte Simulationen, ausgefallene animierte Grafiken, simulationsbasierte Optimierung und Markov-Ketten-Monte-Carlo-Methoden entwickelt.

Simulationsmodelle entwickeln

Simulationsmodelle bestehen aus folgenden Komponenten: Systementitäten, Eingabevariablen, Leistungsmessungen und Funktionsbeziehungen. Im Folgenden finden Sie die Schritte zum Entwickeln eines Simulationsmodells.

Step 1 - Identifizieren Sie das Problem mit einem vorhandenen System oder legen Sie die Anforderungen eines vorgeschlagenen Systems fest.
Step 2 - Entwerfen Sie das Problem unter Berücksichtigung der vorhandenen Systemfaktoren und -einschränkungen.
Step 3 - Sammeln und verarbeiten Sie die Systemdaten unter Beobachtung ihrer Leistung und ihres Ergebnisses.
Step 4 - Entwickeln Sie das Modell mithilfe von Netzwerkdiagrammen und überprüfen Sie es mithilfe verschiedener Überprüfungstechniken.
Step 5 - Validieren Sie das Modell, indem Sie seine Leistung unter verschiedenen Bedingungen mit dem realen System vergleichen.
Step 6 - Erstellen Sie ein Dokument des Modells für die zukünftige Verwendung, das Ziele, Annahmen, Eingabevariablen und Leistung im Detail enthält.
Step 7 - Wählen Sie einen geeigneten Versuchsaufbau gemäß den Anforderungen.
Step 8 - Induzieren Sie experimentelle Bedingungen am Modell und beobachten Sie das Ergebnis.

Simulationsanalyse durchführen

Im Folgenden finden Sie die Schritte zur Durchführung der Simulationsanalyse.

Step 1 - Bereiten Sie eine Problemstellung vor.
Step 2- Wählen Sie Eingabevariablen und erstellen Sie Entitäten für den Simulationsprozess. Es gibt zwei Arten von Variablen - Entscheidungsvariablen und nicht steuerbare Variablen. Entscheidungsvariablen werden vom Programmierer gesteuert, während nicht steuerbare Variablen die Zufallsvariablen sind.
Step 3 - Erstellen Sie Einschränkungen für die Entscheidungsvariablen, indem Sie sie dem Simulationsprozess zuweisen.
Step 4 - Bestimmen Sie die Ausgabevariablen.
Step 5 - Sammeln Sie Daten aus dem realen System, um sie in die Simulation einzugeben.
Step 6 - Entwickeln Sie ein Flussdiagramm, das den Fortschritt des Simulationsprozesses zeigt.
Step 7 - Wählen Sie eine geeignete Simulationssoftware, um das Modell auszuführen.
Step 8 - Überprüfen Sie das Simulationsmodell, indem Sie das Ergebnis mit dem Echtzeitsystem vergleichen.
Step 9 - Führen Sie ein Experiment mit dem Modell durch, indem Sie die Variablenwerte ändern, um die beste Lösung zu finden.
Step 10 - Wenden Sie diese Ergebnisse schließlich auf das Echtzeitsystem an.

Modellierung & Simulation ─ Vorteile

Im Folgenden sind die Vorteile der Verwendung von Modellierung und Simulation aufgeführt:

Easy to understand - Ermöglicht es zu verstehen, wie das System wirklich funktioniert, ohne an Echtzeitsystemen zu arbeiten.
Easy to test - Ermöglicht Änderungen am System und deren Auswirkungen auf die Ausgabe, ohne an Echtzeitsystemen zu arbeiten.
Easy to upgrade - Ermöglicht das Ermitteln der Systemanforderungen durch Anwenden verschiedener Konfigurationen.
Easy to identifying constraints - Ermöglicht die Durchführung von Engpassanalysen, die zu Verzögerungen im Arbeitsprozess, bei Informationen usw. führen.
Easy to diagnose problems- Bestimmte Systeme sind so komplex, dass es nicht einfach ist, ihre Interaktion gleichzeitig zu verstehen. Mit Modeling & Simulation können Sie jedoch alle Wechselwirkungen verstehen und ihre Auswirkungen analysieren. Darüber hinaus können neue Richtlinien, Vorgänge und Verfahren untersucht werden, ohne das reale System zu beeinträchtigen.

Modellierung & Simulation ─ Nachteile

Im Folgenden sind die Nachteile der Verwendung von Modellierung und Simulation aufgeführt:

Das Entwerfen eines Modells ist eine Kunst, die Fachwissen, Schulung und Erfahrung erfordert.
Operationen werden auf dem System unter Verwendung einer Zufallszahl ausgeführt, daher ist es schwierig, das Ergebnis vorherzusagen.
Die Simulation erfordert Personal und ist ein zeitaufwändiger Prozess.
Simulationsergebnisse sind schwer zu übersetzen. Es erfordert Experten zu verstehen.
Simulationsprozess ist teuer.

Modellierung & Simulation ─ Anwendungsbereiche

Modellierung und Simulation können auf die folgenden Bereiche angewendet werden: Militärische Anwendungen, Schulung und Support, Entwurf von Halbleitern, Telekommunikation, Entwürfe und Präsentationen im Tiefbau sowie E-Business-Modelle.

Zusätzlich wird es verwendet, um die interne Struktur eines komplexen Systems wie des biologischen Systems zu untersuchen. Es wird verwendet, um das Systemdesign wie Routing-Algorithmus, Fließband usw. zu optimieren. Es wird zum Testen neuer Designs und Richtlinien verwendet. Es wird verwendet, um analytische Lösungen zu verifizieren.

In diesem Kapitel werden verschiedene Konzepte und Klassifizierungen der Modellierung erörtert.

Modelle & Events

Im Folgenden finden Sie die Grundkonzepte von Modellierung und Simulation.

Object ist eine Einheit, die in der realen Welt existiert, um das Verhalten eines Modells zu untersuchen.
Base Model ist eine hypothetische Erklärung der Objekteigenschaften und ihres Verhaltens, die im gesamten Modell gültig ist.
System ist das artikulierte Objekt unter bestimmten Bedingungen, das in der realen Welt existiert.
Experimental Framewird verwendet, um ein System in der realen Welt zu untersuchen, z. B. experimentelle Bedingungen, Aspekte, Ziele usw. Der grundlegende experimentelle Rahmen besteht aus zwei Variablensätzen - den Rahmeneingabevariablen und den Rahmenausgabevariablen, die dem System oder den Modellterminals entsprechen. Die Frame-Eingabevariable ist dafür verantwortlich, die auf das System oder ein Modell angewendeten Eingaben abzugleichen. Die Frame-Ausgabevariable ist dafür verantwortlich, die Ausgabewerte an das System oder ein Modell anzupassen.
Lumped Model ist eine genaue Erklärung eines Systems, das den spezifizierten Bedingungen eines gegebenen experimentellen Rahmens folgt.
Verificationist der Prozess des Vergleichens von zwei oder mehr Elementen, um deren Genauigkeit sicherzustellen. In Modeling & Simulation kann die Überprüfung durchgeführt werden, indem die Konsistenz eines Simulationsprogramms und des konzentrierten Modells verglichen wird, um deren Leistung sicherzustellen. Es gibt verschiedene Möglichkeiten, einen Validierungsprozess durchzuführen, die wir in einem separaten Kapitel behandeln werden.
Validationist der Prozess des Vergleichs zweier Ergebnisse. In Modeling & Simulation wird die Validierung durchgeführt, indem experimentelle Messungen mit den Simulationsergebnissen im Kontext eines experimentellen Rahmens verglichen werden. Das Modell ist ungültig, wenn die Ergebnisse nicht übereinstimmen. Es gibt verschiedene Möglichkeiten, einen Validierungsprozess durchzuführen, die wir in einem separaten Kapitel behandeln werden.

Systemstatusvariablen

Die Systemstatusvariablen sind ein Datensatz, der erforderlich ist, um den internen Prozess innerhalb des Systems zu einem bestimmten Zeitpunkt zu definieren.

In einem discrete-event modelbleiben die Systemzustandsvariablen über Zeitintervalle konstant und die Werte ändern sich an definierten Punkten, die als Ereigniszeiten bezeichnet werden.
Im continuous-event modelDie Systemzustandsvariablen werden durch Differentialgleichungsergebnisse definiert, deren Wert sich im Laufe der Zeit kontinuierlich ändert.

Im Folgenden sind einige der Systemstatusvariablen aufgeführt:

Entities & Attributes- Eine Entität stellt ein Objekt dar, dessen Wert je nach Prozess mit anderen Entitäten statisch oder dynamisch sein kann. Attribute sind die lokalen Werte, die von der Entität verwendet werden.
Resources- Eine Ressource ist eine Entität, die gleichzeitig eine oder mehrere dynamische Entitäten bedient. Die dynamische Entität kann eine oder mehrere Einheiten einer Ressource anfordern. Wenn dies akzeptiert wird, kann die Entität die Ressource verwenden und nach Abschluss freigeben. Wenn dies abgelehnt wird, kann die Entität einer Warteschlange beitreten.
Lists- Listen werden verwendet, um die Warteschlangen darzustellen, die von den Entitäten und Ressourcen verwendet werden. Je nach Prozess gibt es verschiedene Möglichkeiten für Warteschlangen wie LIFO, FIFO usw.
Delay - Es ist eine unbestimmte Dauer, die durch eine Kombination von Systembedingungen verursacht wird.

Klassifizierung von Modellen

Ein System kann in die folgenden Kategorien eingeteilt werden.

Discrete-Event Simulation Model- In diesem Modell ändern sich die Werte der Zustandsvariablen nur zu bestimmten diskreten Zeitpunkten, zu denen die Ereignisse auftreten. Ereignisse treten nur zur definierten Aktivitätszeit und zu Verzögerungen auf.
Stochastic vs. Deterministic Systems - Stochastische Systeme sind nicht von Zufälligkeit betroffen und ihre Ausgabe ist keine Zufallsvariable, während deterministische Systeme von Zufälligkeit betroffen sind und ihre Ausgabe eine Zufallsvariable ist.
Static vs. Dynamic Simulation- Die statische Simulation umfasst Modelle, die nicht von der Zeit betroffen sind. Zum Beispiel: Monte-Carlo-Modell. Die dynamische Simulation umfasst Modelle, die von der Zeit betroffen sind.
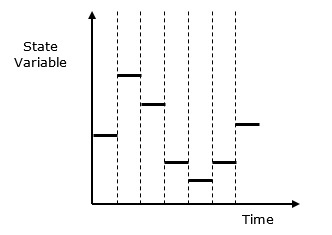
Discrete vs. Continuous Systems- Das diskrete System ist zu einem diskreten Zeitpunkt von den Änderungen der Zustandsvariablen betroffen. Sein Verhalten ist in der folgenden grafischen Darstellung dargestellt.

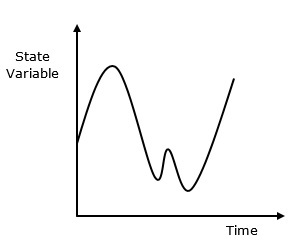
Das kontinuierliche System wird von der Zustandsvariablen beeinflusst, die sich mit der Zeit kontinuierlich ändert. Sein Verhalten ist in der folgenden grafischen Darstellung dargestellt.

Modellierungsprozess

Der Modellierungsprozess umfasst die folgenden Schritte.

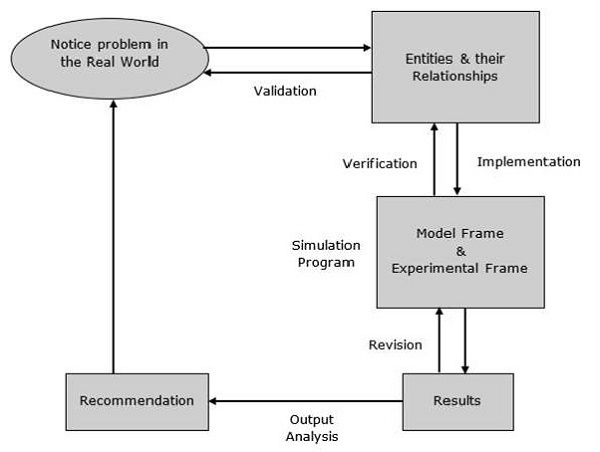
Step 1- Untersuchen Sie das Problem. In dieser Phase müssen wir das Problem verstehen und seine Klassifizierung entsprechend auswählen, z. B. deterministisch oder stochastisch.

Step 2- Entwerfen Sie ein Modell. In dieser Phase müssen wir die folgenden einfachen Aufgaben ausführen, die uns beim Entwerfen eines Modells helfen:

Sammeln Sie Daten gemäß dem Systemverhalten und zukünftigen Anforderungen.
Analysieren Sie die Systemfunktionen, ihre Annahmen und die erforderlichen Maßnahmen, um das Modell erfolgreich zu machen.
Bestimmen Sie die im Modell verwendeten Variablennamen, Funktionen, Einheiten, Beziehungen und deren Anwendungen.
Lösen Sie das Modell mit einer geeigneten Technik und überprüfen Sie das Ergebnis mithilfe von Überprüfungsmethoden. Überprüfen Sie als Nächstes das Ergebnis.
Bereiten Sie einen Bericht vor, der Ergebnisse, Interpretationen, Schlussfolgerungen und Vorschläge enthält.

Step 3- Geben Sie Empfehlungen ab, nachdem Sie den gesamten Prozess in Bezug auf das Modell abgeschlossen haben. Es umfasst Investitionen, Ressourcen, Algorithmen, Techniken usw.

Eines der wirklichen Probleme, mit denen der Simulationsanalyst konfrontiert ist, ist die Validierung des Modells. Das Simulationsmodell ist nur gültig, wenn das Modell eine genaue Darstellung des tatsächlichen Systems ist, andernfalls ist es ungültig.

Validierung und Verifizierung sind die beiden Schritte in jedem Simulationsprojekt, um ein Modell zu validieren.

Validationist der Prozess des Vergleichs zweier Ergebnisse. In diesem Prozess müssen wir die Darstellung eines konzeptionellen Modells mit dem realen System vergleichen. Wenn der Vergleich wahr ist, ist er gültig, andernfalls ungültig.
Verificationist der Prozess des Vergleichs von zwei oder mehr Ergebnissen, um deren Genauigkeit sicherzustellen. In diesem Prozess müssen wir die Implementierung des Modells und die zugehörigen Daten mit der konzeptionellen Beschreibung und den Spezifikationen des Entwicklers vergleichen.

Verifizierungs- und Validierungstechniken

Es gibt verschiedene Techniken zur Überprüfung und Validierung des Simulationsmodells. Im Folgenden sind einige der gängigen Techniken aufgeführt:

Techniken zur Überprüfung des Simulationsmodells

Im Folgenden finden Sie die Möglichkeiten zur Überprüfung des Simulationsmodells:

Durch Verwendung von Programmierkenntnissen zum Schreiben und Debuggen des Programms in Unterprogrammen.
Durch Verwendung der Richtlinie "Strukturierter Rundgang", bei der mehr als eine Person das Programm lesen soll.
Indem Sie die Zwischenergebnisse verfolgen und mit den beobachteten Ergebnissen vergleichen.
Durch Überprüfen der Ausgabe des Simulationsmodells mit verschiedenen Eingabekombinationen.
Durch Vergleichen des endgültigen Simulationsergebnisses mit den Analyseergebnissen.

Techniken zur Validierung des Simulationsmodells

Step 1- Entwerfen Sie ein Modell mit hoher Gültigkeit. Dies kann mit den folgenden Schritten erreicht werden:

Das Modell muss beim Entwerfen mit den Systemexperten besprochen werden.
Das Modell muss während des gesamten Prozesses mit dem Client interagieren.
Die Ausgabe muss von Systemexperten überwacht werden.

Step 2- Testen Sie das Modell anhand von Annahmedaten. Dies kann erreicht werden, indem die Annahmedaten in das Modell übernommen und quantitativ getestet werden. Eine empfindliche Analyse kann auch durchgeführt werden, um den Effekt einer Änderung des Ergebnisses zu beobachten, wenn signifikante Änderungen an den Eingabedaten vorgenommen werden.

Step 3- Bestimmen Sie die repräsentative Ausgabe des Simulationsmodells. Dies kann mit den folgenden Schritten erreicht werden:

Bestimmen Sie, wie nahe die Simulationsausgabe an der tatsächlichen Systemausgabe liegt.
Der Vergleich kann mit dem Turing-Test durchgeführt werden. Es präsentiert die Daten im Systemformat, das nur von Experten erklärt werden kann.
Die statistische Methode kann verwendet werden, um die Modellausgabe mit der tatsächlichen Systemausgabe zu vergleichen.

Modelldatenvergleich mit realen Daten

Nach der Modellentwicklung müssen wir die Ausgabedaten mit den realen Systemdaten vergleichen. Es folgen die beiden Ansätze, um diesen Vergleich durchzuführen.

Validierung des vorhandenen Systems

Bei diesem Ansatz verwenden wir reale Eingaben des Modells, um seine Ausgabe mit der der realen Eingaben des realen Systems zu vergleichen. Dieser Validierungsprozess ist unkompliziert, kann jedoch bei der Durchführung einige Schwierigkeiten bereiten, z. B. wenn die Ausgabe mit der durchschnittlichen Länge, Wartezeit, Leerlaufzeit usw. verglichen werden soll. Sie kann mithilfe statistischer Tests und Hypothesentests verglichen werden. Einige der statistischen Tests sind der Chi-Quadrat-Test, der Kolmogorov-Smirnov-Test, der Cramer-von-Mises-Test und der Moments-Test.

Validierung des Erstmodell

Bedenken Sie, wir müssen ein vorgeschlagenes System beschreiben, das weder gegenwärtig noch in der Vergangenheit existiert. Daher sind keine historischen Daten verfügbar, mit denen die Leistung verglichen werden kann. Daher müssen wir ein hypothetisches System verwenden, das auf Annahmen basiert. Das Befolgen nützlicher Hinweise hilft dabei, die Effizienz zu steigern.

Subsystem Validity- Ein Modell selbst verfügt möglicherweise nicht über ein vorhandenes System, mit dem es verglichen werden kann, kann jedoch aus einem bekannten Subsystem bestehen. Jede dieser Gültigkeiten kann separat geprüft werden.
Internal Validity - Ein Modell mit einem hohen Grad an interner Varianz wird abgelehnt, da ein stochastisches System mit hoher Varianz aufgrund seiner internen Prozesse die Änderungen in der Ausgabe aufgrund von Eingabeänderungen verbirgt.
Sensitivity Analysis - Es liefert die Informationen über die sensitiven Parameter im System, denen wir mehr Aufmerksamkeit schenken müssen.
Face Validity - Wenn das Modell mit entgegengesetzten Logiken arbeitet, sollte es abgelehnt werden, auch wenn es sich wie das reale System verhält.

In diskreten Systemen sind die Änderungen des Systemzustands diskontinuierlich und jede Änderung des Systemzustands wird als bezeichnet event. Das in einer diskreten Systemsimulation verwendete Modell verfügt über eine Reihe von Zahlen zur Darstellung des Systemzustands, die als a bezeichnet werdenstate descriptor. In diesem Kapitel lernen wir auch die Warteschlangensimulation kennen, die neben der Simulation eines Time-Sharing-Systems ein sehr wichtiger Aspekt bei der Simulation diskreter Ereignisse ist.

Es folgt die grafische Darstellung des Verhaltens einer diskreten Systemsimulation.

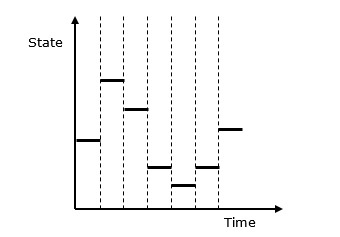
Diskrete Ereignissimulation ─ Hauptmerkmale

Die diskrete Ereignissimulation wird im Allgemeinen von einer Software ausgeführt, die in höheren Programmiersprachen wie Pascal, C ++ oder einer beliebigen speziellen Simulationssprache entwickelt wurde. Im Folgenden sind die fünf Hauptmerkmale aufgeführt:

Entities - Dies sind die Darstellungen realer Elemente wie Maschinenteile.
Relationships - Es bedeutet, Entitäten miteinander zu verbinden.
Simulation Executive - Es ist verantwortlich für die Steuerung der Vorlaufzeit und die Ausführung diskreter Ereignisse.
Random Number Generator - Es hilft, verschiedene Daten zu simulieren, die in das Simulationsmodell eingehen.
Results & Statistics - Es validiert das Modell und liefert seine Leistungsmaßstäbe.

Zeitdiagrammdarstellung

Jedes System hängt von einem Zeitparameter ab. In einer grafischen Darstellung wird es als Uhrzeit oder Zeitzähler bezeichnet und zunächst auf Null gesetzt. Die Zeit wird basierend auf den folgenden zwei Faktoren aktualisiert:

Time Slicing - Dies ist die von einem Modell für jedes Ereignis festgelegte Zeit bis zum Fehlen eines Ereignisses.
Next Event- Dies ist das vom Modell definierte Ereignis für das nächste auszuführende Ereignis anstelle eines Zeitintervalls. Es ist effizienter als Time Slicing.

Simulation eines Warteschlangensystems

Eine Warteschlange ist die Kombination aller Entitäten im System, die bedient werden, und derjenigen, die darauf warten, dass sie an die Reihe kommen.

Parameter

Im Folgenden finden Sie eine Liste der im Warteschlangensystem verwendeten Parameter.

Symbol	Beschreibung
λ	Bezeichnet die Ankunftsrate, dh die Anzahl der Ankünfte pro Sekunde
Ts	Bezeichnet die mittlere Servicezeit für jede Ankunft ohne die Wartezeit in der Warteschlange
σTs	Bezeichnet die Standardabweichung der Servicezeit
ρ	Bezeichnet die Serverzeitauslastung, sowohl im Leerlauf als auch im ausgelasteten Zustand
u	Bezeichnet die Verkehrsintensität
r	Bezeichnet den Mittelwert der Elemente im System
R.	Bezeichnet die Gesamtzahl der Elemente im System
Tr	Bezeichnet die mittlere Zeit eines Elements im System
TR	Bezeichnet die Gesamtzeit eines Elements im System
σr	Bezeichnet die Standardabweichung von r
σTr	Bezeichnet die Standardabweichung von Tr
w	Bezeichnet die durchschnittliche Anzahl der in der Warteschlange wartenden Elemente
σw	Bezeichnet die Standardabweichung von w
Tw	Bezeichnet die mittlere Wartezeit aller Artikel
Td	Bezeichnet die mittlere Wartezeit der in der Warteschlange wartenden Elemente
N.	Bezeichnet die Anzahl der Server in einem System
mx (y)	Bezeichnet das y- ^te Perzentil, was den Wert von y bedeutet, unter dem x y Prozent der Zeit auftritt

Single Server Queue

Dies ist das einfachste Warteschlangensystem, wie in der folgenden Abbildung dargestellt. Das zentrale Element des Systems ist ein Server, der die verbundenen Geräte oder Elemente bedient. Elemente fordern das zu bedienende System an, wenn der Server inaktiv ist. Dann wird es sofort zugestellt, andernfalls tritt es in eine Warteschlange ein. Nachdem die Aufgabe vom Server abgeschlossen wurde, wird der Artikel verlassen.

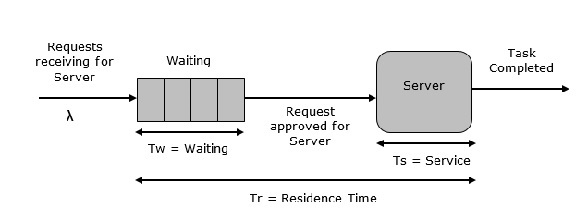
Multi Server Queue

Wie der Name schon sagt, besteht das System aus mehreren Servern und einer gemeinsamen Warteschlange für alle Elemente. Wenn ein Element für den Server angefordert wird, wird es zugewiesen, wenn mindestens ein Server verfügbar ist. Andernfalls beginnt die Warteschlange zu starten, bis der Server frei ist. In diesem System gehen wir davon aus, dass alle Server identisch sind, dh es gibt keinen Unterschied, welcher Server für welches Element ausgewählt wird.

Es gibt eine Ausnahme der Nutzung. LassenN seien Sie also die identischen Server ρist die Auslastung jedes Servers. ErwägenNρdie Nutzung des gesamten Systems zu sein; dann ist die maximale AuslastungN*100%und die maximale Eingaberate ist -

$ λmax = \ frac {\ text {N}} {\ text {T} s} $

Warteschlangenbeziehungen

Die folgende Tabelle zeigt einige grundlegende Warteschlangenbeziehungen.

Allgemeine Geschäftsbedingungen	Einzelner Server	Multi Server
r = λTr Little's Formel	ρ = λTs	ρ = λTs / N.
w = λTw Little Formel	r = w + ρ	u = λTs = ρN
Tr = Tw + Ts		r = w + Nρ

Simulation eines Time-Sharing-Systems

Das Time-Sharing-System ist so konzipiert, dass jeder Benutzer einen kleinen Teil der auf einem System gemeinsam genutzten Zeit verwendet, was dazu führt, dass mehrere Benutzer das System gleichzeitig gemeinsam nutzen. Der Wechsel jedes Benutzers erfolgt so schnell, dass jeder Benutzer das Gefühl hat, sein eigenes System zu verwenden. Es basiert auf dem Konzept der CPU-Planung und der Mehrfachprogrammierung, bei dem mehrere Ressourcen effektiv genutzt werden können, indem mehrere Jobs gleichzeitig auf einem System ausgeführt werden.

Example - SimOS Simulationssystem.

Es wurde von der Stanford University entwickelt, um die komplexen Computerhardware-Designs zu untersuchen, die Anwendungsleistung zu analysieren und die Betriebssysteme zu untersuchen. SimOS enthält eine Software-Simulation aller Hardwarekomponenten moderner Computersysteme, dh Prozessoren, Speicherverwaltungseinheiten (MMU), Caches usw.

Ein kontinuierliches System ist ein System, bei dem wichtige Aktivitäten des Systems ohne Verzögerung reibungslos abgeschlossen werden, dh keine Warteschlange von Ereignissen, keine Sortierung der Zeitsimulation usw. Wenn ein kontinuierliches System mathematisch modelliert wird, werden seine Variablen, die die Attribute darstellen, durch kontinuierliche Funktionen gesteuert .

Was ist kontinuierliche Simulation?

Kontinuierliche Simulation ist eine Art von Simulation, bei der sich Zustandsvariablen zeitlich kontinuierlich ändern. Es folgt die grafische Darstellung seines Verhaltens.

Warum kontinuierliche Simulation verwenden?

Wir müssen eine kontinuierliche Simulation verwenden, da diese von der Differentialgleichung verschiedener mit dem System verbundener Parameter und ihren uns bekannten geschätzten Ergebnissen abhängt.

Anwendungsbereiche

Kontinuierliche Simulation wird in den folgenden Sektoren verwendet. Im Tiefbau für den Bau von Damm- und Tunnelbauten. In militärischen Anwendungen zur Simulation der Flugbahn von Raketen, zur Simulation des Trainings von Kampfflugzeugen und zum Entwerfen und Testen intelligenter Steuerungen für Unterwasserfahrzeuge.

In der Logistik für die Gestaltung des Mautplatzes, der Passagierflussanalyse am Flughafenterminal und der proaktiven Bewertung des Flugplans. In der Geschäftsentwicklung für Produktentwicklungsplanung, Personalmanagementplanung und Marktstudienanalyse.

Die Monte-Carlo-Simulation ist eine computergestützte mathematische Technik zur Erzeugung von Zufallsstichproben auf der Grundlage einer bekannten Verteilung für numerische Experimente. Diese Methode wird bei quantitativen Risikoanalysen und Entscheidungsproblemen angewendet. Diese Methode wird von Fachleuten verschiedener Profile wie Finanzen, Projektmanagement, Energie, Fertigung, Ingenieurwesen, Forschung und Entwicklung, Versicherung, Öl und Gas, Transport usw. verwendet.

Diese Methode wurde erstmals 1940 von Wissenschaftlern verwendet, die an der Atombombe arbeiteten. Diese Methode kann in Situationen angewendet werden, in denen wir eine Schätzung und unsichere Entscheidungen treffen müssen, z. B. Wettervorhersagen.

Monte-Carlo-Simulation ─ Wichtige Eigenschaften

Im Folgenden sind die drei wichtigen Merkmale der Monte-Carlo-Methode aufgeführt:

Seine Ausgabe muss Zufallsstichproben erzeugen.
Die Eingangsverteilung muss bekannt sein.
Das Ergebnis muss während der Durchführung eines Experiments bekannt sein.

Monte-Carlo-Simulation ─ Vorteile

Einfach zu implementieren.
Bietet statistische Stichproben für numerische Experimente mit dem Computer.
Bietet eine ungefähre Lösung für mathematische Probleme.
Kann sowohl für stochastische als auch für deterministische Probleme verwendet werden.

Monte-Carlo-Simulation ─ Nachteile

Zeitaufwendig, da eine große Anzahl von Abtastungen erzeugt werden muss, um die gewünschte Ausgabe zu erhalten.
Die Ergebnisse dieser Methode sind nur die Annäherung der wahren Werte, nicht die exakten.

Monte-Carlo-Simulationsmethode ─ Flussdiagramm

Die folgende Abbildung zeigt ein verallgemeinertes Flussdiagramm der Monte-Carlo-Simulation.

Das Ziel der Datenbank in Modeling & Simulation ist es, die Datendarstellung und ihre Beziehung für Analyse- und Testzwecke bereitzustellen. Das erste Datenmodell wurde 1980 von Edgar Codd eingeführt. Es folgten die herausragenden Merkmale des Modells.

Datenbank ist die Sammlung verschiedener Datenobjekte, die die Informationen und ihre Beziehungen definieren.
Regeln dienen zum Definieren der Einschränkungen für Daten in den Objekten.
Operationen können auf Objekte zum Abrufen von Informationen angewendet werden.

Anfänglich basierte die Datenmodellierung auf dem Konzept von Entitäten und Beziehungen, bei denen die Entitäten Arten von Dateninformationen sind und Beziehungen die Assoziationen zwischen den Entitäten darstellen.

Das neueste Konzept für die Datenmodellierung ist das objektorientierte Design, bei dem Entitäten als Klassen dargestellt werden, die als Vorlagen in der Computerprogrammierung verwendet werden. Eine Klasse mit Namen, Attributen, Einschränkungen und Beziehungen zu Objekten anderer Klassen.

Die grundlegende Darstellung sieht aus wie -

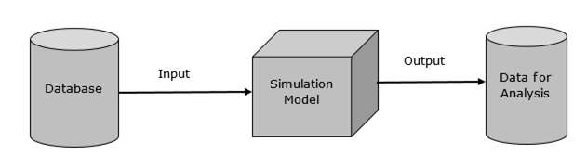
Daten Präsentation

Datendarstellung für Ereignisse

Ein Simulationsereignis hat seine Attribute wie den Ereignisnamen und die zugehörigen Zeitinformationen. Es stellt die Ausführung einer bereitgestellten Simulation unter Verwendung eines Satzes von Eingabedaten dar, die dem Parameter der Eingabedatei zugeordnet sind, und liefert das Ergebnis als Satz von Ausgabedaten, die in mehreren Dateien gespeichert sind, die den Datendateien zugeordnet sind.

Datendarstellung für Eingabedateien

Jeder Simulationsprozess erfordert einen anderen Satz von Eingabedaten und die zugehörigen Parameterwerte, die in der Eingabedatendatei dargestellt werden. Die Eingabedatei ist der Software zugeordnet, die die Simulation verarbeitet. Das Datenmodell repräsentiert die referenzierten Dateien durch eine Zuordnung zu einer Datendatei.

Datendarstellung für Ausgabedateien

Wenn der Simulationsprozess abgeschlossen ist, werden verschiedene Ausgabedateien erstellt und jede Ausgabedatei wird als Datendatei dargestellt. Jede Datei hat ihren Namen, ihre Beschreibung und einen universellen Faktor. Eine Datendatei wird in zwei Dateien klassifiziert. Die erste Datei enthält die numerischen Werte und die zweite Datei enthält die beschreibenden Informationen für den Inhalt der numerischen Datei.

Neuronale Netze in Modellierung und Simulation

Das neuronale Netz ist der Zweig der künstlichen Intelligenz. Das neuronale Netzwerk ist ein Netzwerk von vielen Prozessoren, die als Einheiten bezeichnet werden, wobei jede Einheit ihren kleinen lokalen Speicher hat. Jede Einheit ist durch unidirektionale Kommunikationskanäle verbunden, die als Verbindungen bezeichnet werden und die numerischen Daten tragen. Jede Einheit arbeitet nur mit ihren lokalen Daten und den Eingaben, die sie von den Verbindungen erhalten.

Geschichte

Die historische Perspektive der Simulation ist in chronologischer Reihenfolge aufgezählt.

Das erste neuronale Modell wurde in entwickelt 1940 von McCulloch & Pitts.

Im 1949Donald Hebb schrieb ein Buch „The Organization of Behavior“, das auf das Konzept der Neuronen hinwies.

Im 1950Mit der Weiterentwicklung der Computer wurde es möglich, ein Modell dieser Theorien zu erstellen. Es wurde von IBM Forschungslabors durchgeführt. Die Bemühungen scheiterten jedoch und spätere Versuche waren erfolgreich.

Im 1959Bernard Widrow und Marcian Hoff entwickelten Modelle namens ADALINE und MADALINE. Diese Modelle verfügen über mehrere ADAptive LINear-Elemente. MADALINE war das erste neuronale Netzwerk, das auf ein reales Problem angewendet wurde.

Im 1962Das Perzeptronmodell wurde von Rosenblatt entwickelt und hat die Fähigkeit, einfache Musterklassifizierungsprobleme zu lösen.

Im 1969, Minsky & Papert lieferten einen mathematischen Beweis für die Einschränkungen des Perzeptronmodells bei der Berechnung. Es wurde gesagt, dass das Perzeptronmodell das X-OR-Problem nicht lösen kann. Solche Nachteile führten zu einem vorübergehenden Rückgang der neuronalen Netze.

Im 1982John Hopfield von Caltech präsentierte seine Ideen auf Papier der National Academy of Sciences, um Maschinen mit bidirektionalen Linien herzustellen. Bisher wurden unidirektionale Linien verwendet.

Wenn traditionelle Techniken der künstlichen Intelligenz mit symbolischen Methoden versagen, besteht die Notwendigkeit, neuronale Netze zu verwenden. Neuronale Netze verfügen über massive Parallelitätstechniken, die die zur Lösung solcher Probleme erforderliche Rechenleistung bereitstellen.

Anwendungsbereiche

Neuronale Netze können in Sprachsynthesegeräten zur Mustererkennung, zur Erkennung diagnostischer Probleme, in Robotersteuerplatinen und medizinischen Geräten verwendet werden.

Fuzzy Set in Modellierung & Simulation

Wie bereits erwähnt, hängt jeder Prozess der kontinuierlichen Simulation von Differentialgleichungen und deren Parametern wie a, b, c, d> 0 ab. Im Allgemeinen werden Punktschätzungen berechnet und im Modell verwendet. Manchmal sind diese Schätzungen jedoch unsicher, sodass wir Fuzzy-Zahlen in Differentialgleichungen benötigen, die die Schätzungen der unbekannten Parameter liefern.

Was ist ein Fuzzy-Set?

In einer klassischen Menge ist ein Element entweder ein Mitglied der Menge oder nicht. Fuzzy-Mengen werden als klassische Mengen definiertX als -

A = {(x, μA (x)) | x ∈ X}

Case 1 - Die Funktion μA(x) hat die folgenden Eigenschaften -

∀x ∈ X μA (x) ≥ 0

sup x ∈ X {μA (x)} = 1

Case 2 - Fuzzy setzen lassen B definiert werden als A = {(3, 0.3), (4, 0.7), (5, 1), (6, 0.4)}, dann wird seine Standard-Fuzzy-Notation geschrieben als A = {0.3/3, 0.7/4, 1/5, 0.4/6}

Ein Wert mit einer Mitgliedschaftsstufe von Null wird im Ausdruck der Menge nicht angezeigt.

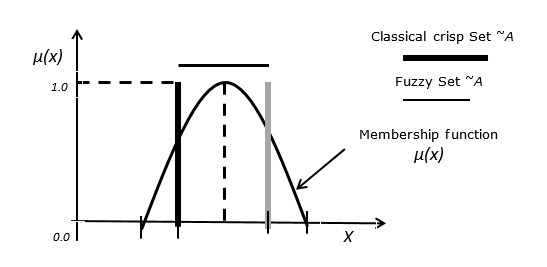
Case 3 - Beziehung zwischen Fuzzy-Set und klassischem Crisp-Set.

Die folgende Abbildung zeigt die Beziehung zwischen einem Fuzzy-Set und einem klassischen Crisp-Set.