Zeichnen rationaler Zahlen auf einer Zahlenlinie

Eine rationale Zahl ist ein Bruch und wird wie folgt auf einer Zahlenlinie aufgetragen.

Basic rules of representing rational no. on number line

• Wenn die rationale Nr. (Bruch) richtig ist, liegt sie zwischen 0 und 1.

• Wenn die rationale Nr. (Bruch) unpassend ist, konvertieren wir sie zuerst in eine gemischte Fraktion und dann in die gegebene rationale Nr. liegt zwischen der ganzen Zahl und der nächsten ganzen Zahl.

Wir verwenden die folgenden Schritte, um eine rationale Zahl oder einen rationalen Bruch darzustellen, z. B. $ \ frac {5} {7} $ in der Zahlenreihe.

Step 1 - Wir ziehen eine Zahlenlinie.

Step 2- Da die Zahl $ \ frac {5} {7} $ eine positive Zahl ist, liegt sie auf der rechten Seite von Null.

Step 3- Nach der Nullmarke haben wir also $ \ frac {1} {7}, \: \ frac {2} {7}, \: \ frac {3} {7}, \: \ frac {4} {7 }, \: \ frac {5} {7}, \: \ frac {6} {7}, $ und ( $ \ frac {7} {7} $ = 1).

Step 4- Die rationale Zahl $ \ frac {5} {7} $ in der Zahlenreihe wird wie folgt angezeigt.

Zeichnen Sie $ \ frac {1} {4} $ und $ 1 \ frac {2} {4} $ in die Zahlenzeile unten

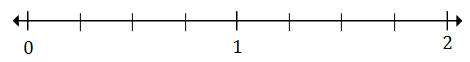
Lösung

Step 1:

$ \ frac {1} {4} $ (A) liegt zwischen 0 und 1; $ 1 \ frac {2} {4} $ (B) liegt zwischen 1 und 2

Step 2:

Jede Unterteilung ist in vier Teile unterteilt, da der Boden der Brüche 4 ist.

$ \ frac {1} {4} $ ist die erste Markierung nach 0, daher steht Punkt A für $ \ frac {1} {4} $

$ 1 \ frac {2} {4} $ ist die zweite Markierung nach 1, daher steht Punkt B für $ 1 \ frac {2} {4} $

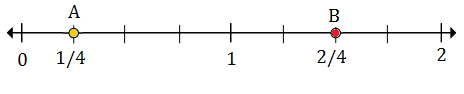
Zeichnen Sie $ \ frac {5} {8} $ und $ 2 \ frac {3} {8} $ in die Zahlenzeile unten

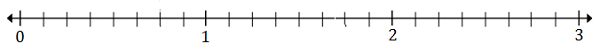
Lösung

Step 1:

$ \ frac {5} {8} $ 8 (A) liegt zwischen 0 und 1; $ 2 \ frac {3} {8} $ (B) liegt zwischen 2 und 3

Step 2:

Jede Unterteilung ist in acht Teile unterteilt, da der Boden der Brüche 8 beträgt.

$ \ frac {5} {8} $ ist die fünfte Markierung nach 0, daher steht Punkt A für $ \ frac {5} {8} $

$ 2 \ frac {3} {8} $ ist die dritte Markierung nach 2, daher steht Punkt B für $ 2 \ frac {3} {8} $