Seaborn - Lineare Beziehungen

In den meisten Fällen verwenden wir Datensätze, die mehrere quantitative Variablen enthalten, und das Ziel einer Analyse besteht häufig darin, diese Variablen miteinander in Beziehung zu setzen. Dies kann über die Regressionslinien erfolgen.

Beim Erstellen der Regressionsmodelle prüfen wir häufig, ob multicollinearity,wo wir die Korrelation zwischen allen Kombinationen kontinuierlicher Variablen sehen mussten und die notwendigen Maßnahmen ergreifen werden, um Multikollinearität zu entfernen, falls vorhanden. In solchen Fällen helfen die folgenden Techniken.

Funktionen zum Zeichnen linearer Regressionsmodelle

In Seaborn gibt es zwei Hauptfunktionen, um eine durch Regression bestimmte lineare Beziehung zu visualisieren. Diese Funktionen sindregplot() und lmplot().

regplot vs lmplot

neu planen	lmplot
Akzeptiert die x- und y-Variablen in einer Vielzahl von Formaten, einschließlich einfacher Numpy-Arrays, Pandas Series-Objekte oder als Verweise auf Variablen in einem Pandas DataFrame	hat Daten als erforderlichen Parameter und die Variablen x und y müssen als Zeichenfolgen angegeben werden. Dieses Datenformat wird als "Langform" -Daten bezeichnet

Lassen Sie uns nun die Handlungen zeichnen.

Beispiel

Zeichnen Sie den Regplot und dann den lmplot mit denselben Daten in diesem Beispiel

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('tips')
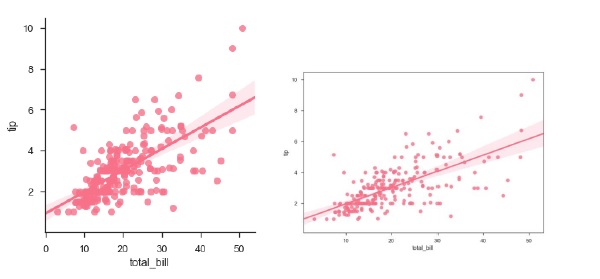
sb.regplot(x = "total_bill", y = "tip", data = df)
sb.lmplot(x = "total_bill", y = "tip", data = df)
plt.show()

Ausgabe

Sie können den Unterschied in der Größe zwischen zwei Plots sehen.

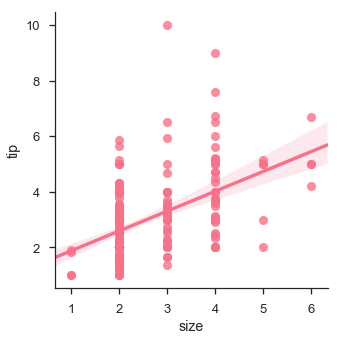
Wir können auch eine lineare Regression anpassen, wenn eine der Variablen diskrete Werte annimmt

Beispiel

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('tips')
sb.lmplot(x = "size", y = "tip", data = df)
plt.show()

Ausgabe

Anpassen verschiedener Arten von Modellen

Das oben verwendete einfache lineare Regressionsmodell ist sehr einfach anzupassen, aber in den meisten Fällen sind die Daten nicht linear und die obigen Methoden können die Regressionslinie nicht verallgemeinern.

Verwenden wir den Datensatz von Anscombe mit den Regressionsdiagrammen -

Beispiel

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('anscombe')
sb.lmplot(x="x", y="y", data=df.query("dataset == 'I'"))
plt.show()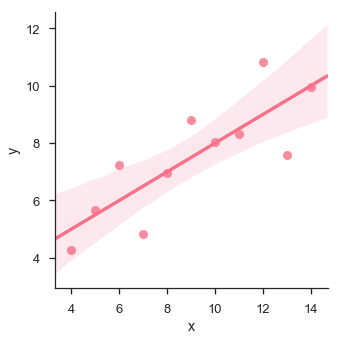

In diesem Fall passen die Daten gut für ein lineares Regressionsmodell mit geringerer Varianz.

Lassen Sie uns ein anderes Beispiel sehen, bei dem die Daten eine hohe Abweichung aufweisen, was zeigt, dass die Linie der besten Anpassung nicht gut ist.

Beispiel

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('anscombe')
sb.lmplot(x = "x", y = "y", data = df.query("dataset == 'II'"))
plt.show()

Ausgabe

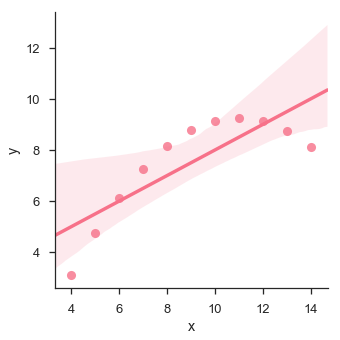
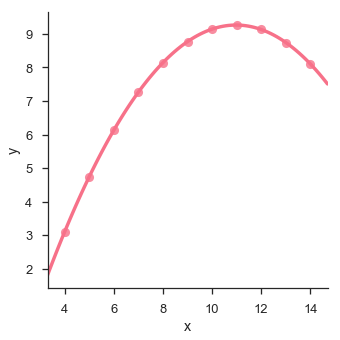
Das Diagramm zeigt die hohe Abweichung der Datenpunkte von der Regressionslinie. Eine solche nichtlineare höhere Ordnung kann mit dem visualisiert werdenlmplot() und regplot()Dies kann in ein Polynom-Regressionsmodell passen, um einfache Arten nichtlinearer Trends im Datensatz zu untersuchen.

Beispiel

import pandas as pd
import seaborn as sb
from matplotlib import pyplot as plt
df = sb.load_dataset('anscombe')
sb.lmplot(x = "x", y = "y", data = df.query("dataset == 'II'"),order = 2)
plt.show()

Ausgabe