Verwenden eines Netzes, um die Oberfläche eines dreieckigen Prismas zu ermitteln

Einführung

In dieser Lektion verwenden wir Netze eines Dreiecksprismas, um die Oberfläche des Dreiecksprismas zu ermitteln.

Das net einer festen Figur wird gebildet, wenn eine feste Figur entlang ihrer Kanten entfaltet wird und ihre Flächen in einem Muster in zwei Dimensionen angeordnet sind.

Netze dreieckiger Prismen bestehen aus Rechtecken und Dreiecken.

Using a net to find the surface area of a rectangular prism

Das Finden der Flächen jedes der Rechtecke und Dreiecke des Netzes eines dreieckigen Prismas und das Addieren dieser Flächen ergibt die Oberfläche oder die Gesamtoberfläche des dreieckigen Prismas.

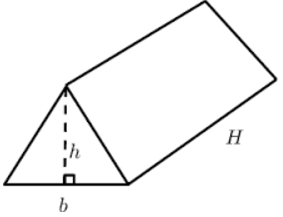
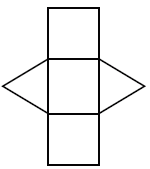
Angenommen, die Beine eines rechtwinkligen Dreiecks, das die Basis eines dreieckigen Prismas bildet, sind 3 und 4 Einheiten, und die Höhe des Prismas beträgt 10 Einheiten. Aus dem Netz können wir sehen, dass es zwei kongruente Dreiecksflächen und drei rechteckige Flächen gibt, deren Flächen wie folgt sind. 6 quadratische Einheiten und (3 + 4 + 5) 10 = 120 quadratische Einheiten. Die Oberfläche des Prismas ist dann = 2 (6) + 120 = 132 quadratische Einheiten.

Surface Area of a Triangular Prism using Nets

Beispiel 1:

Finden Sie die Oberfläche des folgenden dreieckigen Prismas mit net.