Volumen de un sólido hecho de cubos con longitudes de borde de fracción unitaria

Introducción

Aquí encontramos el volumen de sólidos hechos de cubos con longitudes de borde de fracción unitaria. Considere, por ejemplo, un sólido de dimensiones 3 en × 3 en × 3 hecho de pequeños cubos con longitudes de borde de $ \ frac {1} {2} $ pulgadas.

En ese caso, el sólido se compone de 6 × 6 × 6 cubos pequeños de $ \ frac {1} {2} $ pulgadas de longitud de borde. Entonces, el volumen del sólido en este caso sería

Volumen = lwh = $ 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} $

= 3 × 3 × 3 = 27 pulgadas cúbicas

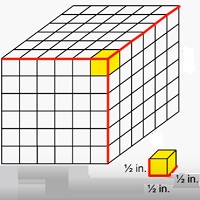
Fórmula para el volumen de sólido hecho de cubos con longitudes de borde fraccionarias unitarias

Suponiendo que el sólido es un cubo de arista a unidades

b = número de cubos con unidad de longitud fraccionaria de borde a lo largo de cada borde

k = unidad de longitud fraccionaria del borde

Volume of solid = b × k × b × k × b × k cubic units

Ejemplo 1

Encuentre el volumen del siguiente sólido de cubos con longitudes de arista de fracción unitaria. Cada unidad de prismas se mide en cm (no a escala)

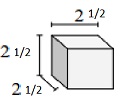
Solución

Step 1:

Sólido de cubos con longitudes de arista de fracción unitaria de $ \ frac {1} {2} $ cm

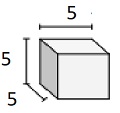
Step 2:

Volumen V = lwh = $ 2 \ frac {1} {2} \ times 2 \ frac {1} {2} \ times 2 \ frac {1} {2} $

= $ 5 \ veces \ frac {1} {2} \ veces 5 \ veces \ frac {1} {2} \ veces 5 \ veces \ frac {1} {2} $

= $ 15 \ frac {5} {8} $ cu cm

Ejemplo 2

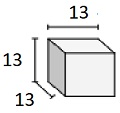
Encuentre el volumen del siguiente sólido de cubos con longitudes de arista de fracción unitaria. Cada unidad de prismas se mide en cm (no a escala)

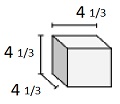
Solución

Step 1:

Sólido de cubos con longitudes de arista de fracción unitaria de $ \ frac {1} {3} $ cm

Step 2:

Volumen V = lwh = $ 4 \ frac {1} {3} \ times 4 \ frac {1} {3} \ times 4 \ frac {1} {3} $

= $ 13 \ veces \ frac {1} {3} \ veces 13 \ veces \ frac {1} {3} \ veces 13 \ veces \ frac {1} {3} $

= $ 81 \ frac {10} {27} $ cu cm