DAA: gráfico de varias etapas
Un gráfico de varias etapas G = (V, E) es un gráfico dirigido donde los vértices se dividen en k (dónde k > 1) número de subconjuntos disjuntos S = {s1,s2,…,sk}tal que el borde (u, v) está en E, entonces u Є s i y v Є s 1 + 1 para algunos subconjuntos en la partición y |s1| = |sk| = 1.
El vértice s Є s1 se llama el source y el vértice t Є sk se llama sink.
Ggeneralmente se asume que es un gráfico ponderado. En este gráfico, el costo de una arista (i, j) está representado por c (i, j) . Por lo tanto, el costo de la ruta desde la fuentes hundir t es la suma de los costos de cada borde en este camino.
El problema del gráfico de varias etapas es encontrar la ruta con un costo mínimo desde la fuente s hundir t.
Ejemplo
Considere el siguiente ejemplo para comprender el concepto de gráfico de varias etapas.
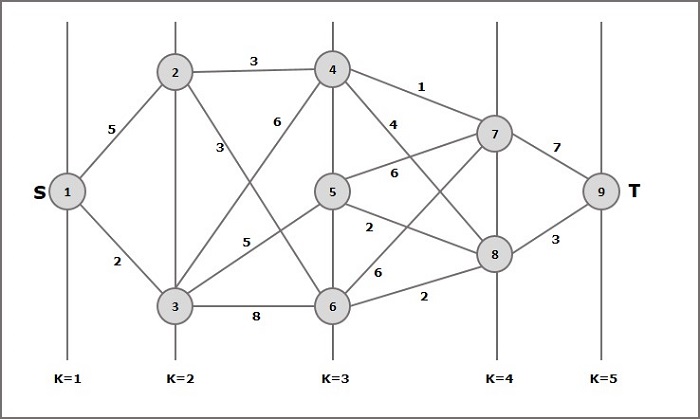
Según la fórmula, tenemos que calcular el costo (i, j) usando los siguientes pasos
Paso 1: Costo (K-2, j)
En este paso, se seleccionan tres nodos (nodo 4, 5. 6) como j. Por lo tanto, tenemos tres opciones para elegir el costo mínimo en este paso.
Costo (3, 4) = mínimo {c (4, 7) + Costo (7, 9), c (4, 8) + Costo (8, 9)} = 7
Costo (3, 5) = mínimo {c (5, 7) + Costo (7, 9), c (5, 8) + Costo (8, 9)} = 5
Costo (3, 6) = mínimo {c (6, 7) + Costo (7, 9), c (6, 8) + Costo (8, 9)} = 5
Paso 2: Costo (K-3, j)
Se seleccionan dos nodos como j porque en la etapa k - 3 = 2 hay dos nodos, 2 y 3. Entonces, el valor i = 2 y j = 2 y 3.
Coste (2, 2) = min {c (2, 4) + Coste (4, 8) + Coste (8, 9), c (2, 6) +
Costo (6, 8) + Costo (8, 9)} = 8
Costo (2, 3) = {c (3, 4) + Costo (4, 8) + Costo (8, 9), c (3, 5) + Costo (5, 8) + Costo (8, 9), c (3, 6) + Costo (6, 8) + Costo (8, 9)} = 10
Paso 3: Costo (K-4, j)
Costo (1, 1) = {c (1, 2) + Costo (2, 6) + Costo (6, 8) + Costo (8, 9), c (1, 3) + Costo (3, 5) + Costo (5, 8) + Costo (8, 9))} = 12
c (1, 3) + Costo (3, 6) + Costo (6, 8 + Costo (8, 9))} = 13
Por lo tanto, la ruta que tiene el costo mínimo es 1→ 3→ 5→ 8→ 9.