DAA - Cubierta de vértice
Una cobertura de vértice de un gráfico no dirigido G = (V, E) es un subconjunto de vértices V' ⊆ V tal que si borde (u, v) es un borde de G, entonces tambien u en V o v en V' o ambos.
Encuentre una cobertura de vértice de tamaño máximo en un gráfico no dirigido dado. Esta cobertura de vértice óptima es la versión de optimización de un problema NP-completo. Sin embargo, no es demasiado difícil encontrar una cobertura de vértices cercana a la óptima.
APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G]
while E' is not empty do
Let (u, v) be an arbitrary edge of E' c ← c U {u, v}
Remove from E' every edge incident on either u or v
return cEjemplo
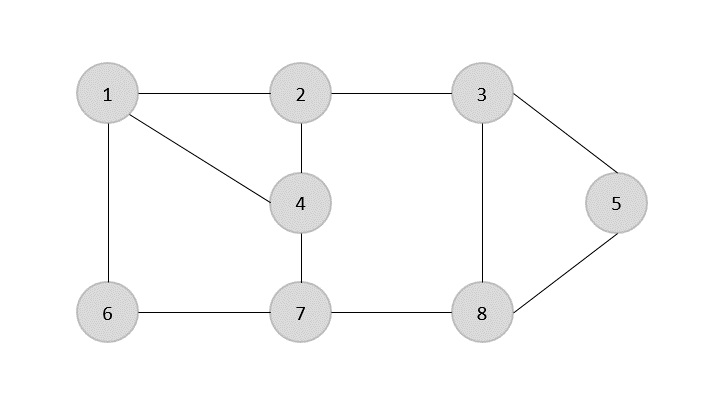
El conjunto de aristas del gráfico dado es:
{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}
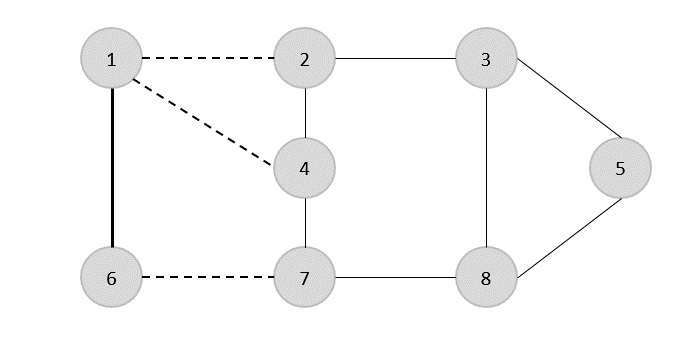
Ahora, comenzamos seleccionando un borde arbitrario (1,6). Eliminamos todas las aristas, que son incidentes al vértice 1 o 6 y agregamos la arista (1,6) para cubrir.
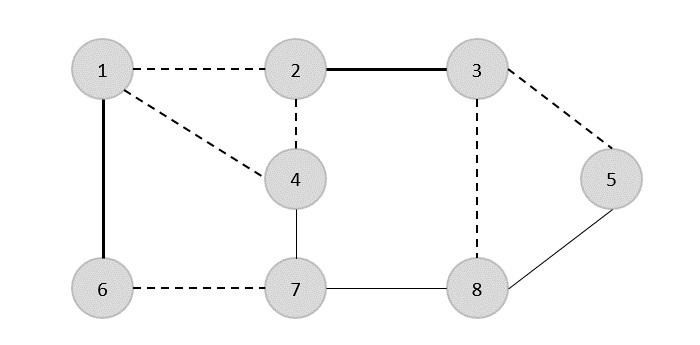
En el siguiente paso, hemos elegido otra arista (2,3) al azar
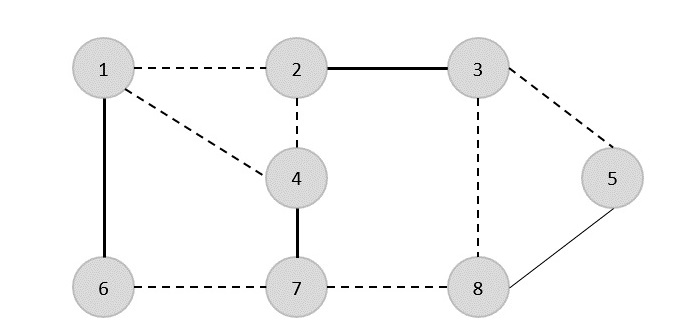
Ahora seleccionamos otro borde (4,7).
Seleccionamos otro borde (8,5).
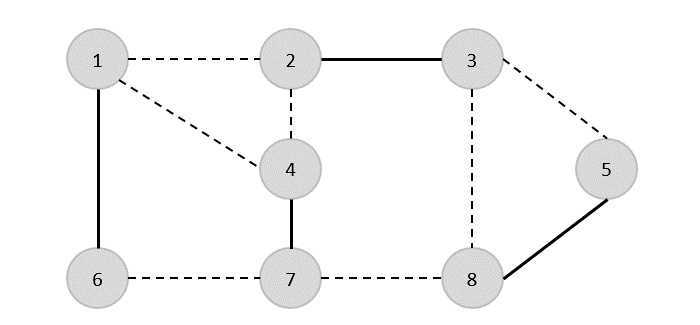
Por lo tanto, la cobertura de vértices de este gráfico es {1,2,4,5}.
Análisis
Es fácil ver que el tiempo de ejecución de este algoritmo es O(V + E), usando la lista de adyacencia para representar E'.