Procesamiento de señal digital - Guía rápida
Definición
Todo lo que lleve información puede llamarse señal. También se puede definir como una cantidad física que varía con el tiempo, la temperatura, la presión o con cualquier variable independiente como la señal de voz o la señal de video.
El proceso de funcionamiento en el que las características de una señal (amplitud, forma, fase, frecuencia, etc.) sufren un cambio se conoce como procesamiento de señales.
Note- Cualquier señal no deseada que interfiera con la señal principal se denomina ruido. Entonces, el ruido también es una señal pero no deseada.
De acuerdo con su representación y procesamiento, las señales se pueden clasificar en varias categorías cuyos detalles se describen a continuación.
Señales de tiempo continuas
Las señales de tiempo continuo se definen a lo largo de un continuo de tiempo y, por lo tanto, están representadas por una variable independiente continua. Las señales de tiempo continuo a menudo se denominan señales analógicas.
Este tipo de señal muestra continuidad tanto en amplitud como en tiempo. Estos tendrán valores en cada instante de tiempo. Las funciones seno y coseno son el mejor ejemplo de señal de tiempo continuo.
La señal que se muestra arriba es un ejemplo de señal de tiempo continuo porque podemos obtener el valor de la señal en cada instante de tiempo.
Señales de tiempo discretas
Las señales, que se definen en tiempos discretos, se conocen como señales discretas. Por tanto, cada variable independiente tiene un valor distinto. Por lo tanto, se representan como una secuencia de números.
Aunque las señales de voz y video tienen el privilegio de ser representadas en formato de tiempo tanto continuo como discreto; en determinadas circunstancias, son idénticas. Las amplitudes también muestran características discretas. Un ejemplo perfecto de esto es una señal digital; cuya amplitud y tiempo son ambos discretos.
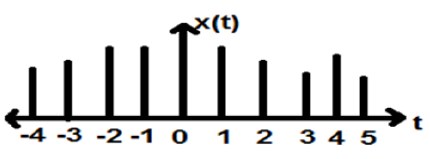
La figura anterior muestra la característica de amplitud discreta de una señal discreta durante un período de tiempo. Matemáticamente, estos tipos de señales se pueden formular como;
$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$Donde, n es un número entero.
Es una secuencia de números x, donde el n- ésimo número de la secuencia se representa como x [n].
Para probar un sistema, generalmente se utilizan señales estándar o básicas. Estas señales son los componentes básicos de muchas señales complejas. Por tanto, juegan un papel muy importante en el estudio de señales y sistemas.
Unidad de impulso o función delta
Una señal, que satisface la condición, $\delta(t) = \lim_{\epsilon \to \infty} x(t)$se conoce como señal de impulso unitario. Esta señal tiende al infinito cuando t = 0 y tiende a cero cuando t ≠ 0, de modo que el área bajo su curva es siempre igual a uno. La función delta tiene amplitud cero en todas partes excunit_impulse.jpgept en t = 0.

Propiedades de la señal de impulso unitario
- δ (t) es una señal par.
- δ (t) es un ejemplo de señal sin energía ni potencia (NENP).
- El área de la señal de impulso unitario se puede escribir como; $$A = \int_{-\infty}^{\infty} \delta (t)dt = \int_{-\infty}^{\infty} \lim_{\epsilon \to 0} x(t) dt = \lim_{\epsilon \to 0} \int_{-\infty}^{\infty} [x(t)dt] = 1$$
- El peso o la fuerza de la señal se pueden escribir como; $$y(t) = A\delta (t)$$
- El área de la señal de impulso ponderada se puede escribir como: $$y (t) = \int_{-\infty}^{\infty} y (t)dt = \int_{-\infty}^{\infty} A\delta (t) = A[\int_{-\infty}^{\infty} \delta (t)dt ] = A = 1 = Wigthedimpulse$$
Señal de paso de unidad
Una señal que cumple las siguientes dos condiciones:
- $U(t) = 1(when\quad t \geq 0 )and$
- $U(t) = 0 (when\quad t < 0 )$
se conoce como señal de paso unitario.
Tiene la propiedad de mostrar discontinuidad en t = 0. En el punto de discontinuidad, el valor de la señal viene dado por el promedio del valor de la señal. Esta señal se ha tomado justo antes y después del punto de discontinuidad (según los Fenómenos de Gibb).
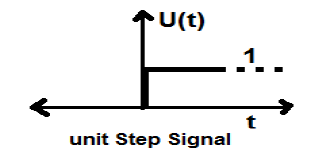
Si agregamos una señal de paso a otra señal de paso que tiene una escala de tiempo, el resultado será la unidad. Es una señal de tipo de potencia y el valor de potencia es 0,5. El valor RMS (raíz cuadrada media) es 0,707 y su valor medio también es 0,5
Señal de rampa
La integración de la señal de paso da como resultado una señal de rampa. Está representado por r (t). La señal de rampa también satisface la condición$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$. No es una señal de tipo energía ni potencia (NENP).
Señal parabólica
La integración de la señal de rampa conduce a una señal parabólica. Está representado por p (t). La señal parabólica también satisface la condición$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$. No es una señal de tipo energía ni potencia (NENP).
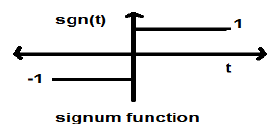
Función Signum
Esta función se representa como
$$sgn(t) = \begin{cases}1 & for\quad t >0\\-1 & for\quad t<0\end{cases}$$Es una señal de tipo de potencia. Su valor de potencia y los valores RMS (raíz cuadrada media), ambos son 1. El valor promedio de la función signum es cero.
Función Sinc
También es una función del seno y se escribe como:
$$SinC(t) = \frac{Sin\Pi t}{\Pi T} = Sa(\Pi t)$$Propiedades de la función Sinc
Es una señal de tipo de energía.
$Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$
$Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$ (El rango de sinπ∞ varía entre -1 y +1, pero cualquier cosa dividida por infinito es igual a cero)
-
Si $ \sin c(t) = 0 => \sin \Pi t = 0$
$\Rightarrow \Pi t = n\Pi$
$\Rightarrow t = n (n \neq 0)$
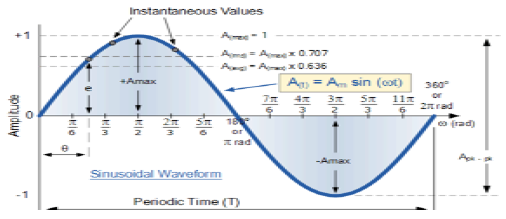
Señal sinusoidal
Una señal, que es de naturaleza continua, se conoce como señal continua. El formato general de una señal sinusoidal es
$$x(t) = A\sin (\omega t + \phi )$$Aquí,
A = amplitud de la señal
ω = Frecuencia angular de la señal (medida en radianes)
φ = Ángulo de fase de la señal (medido en radianes)
La tendencia de esta señal es repetirse después de cierto período de tiempo, por eso se llama señal periódica. El período de tiempo de la señal se da como;
$$T = \frac{2\pi }{\omega }$$La vista esquemática de la señal sinusoidal se muestra a continuación.
Función rectangular
Se dice que una señal es del tipo de función rectangular si satisface la siguiente condición:
$$\pi(\frac{t}{\tau}) = \begin{cases}1, & for\quad t\leq \frac{\tau}{2}\\0, & Otherwise\end{cases}$$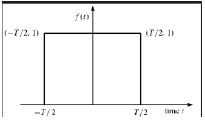
Al ser simétrica con respecto al eje Y, esta señal se denomina señal par.
Señal de pulso triangular
Cualquier señal que cumpla la siguiente condición se conoce como señal triangular.
$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & for|t|<\frac{\tau}{2}\\0 & for|t|>\frac{\tau}{2}\end{cases}$$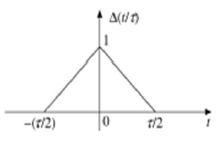
Esta señal es simétrica con respecto al eje Y. Por lo tanto, también se denomina señal par.
Hemos visto cómo se pueden representar las señales básicas en el dominio del tiempo continuo. Veamos cómo se pueden representar las señales básicas en el dominio de tiempo discreto.
Secuencia de impulso unitario
Se denota como δ (n) en el dominio del tiempo discreto y se puede definir como;
$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$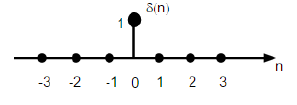
Señal de paso de unidad
La señal de paso de unidad de tiempo discreta se define como;
$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$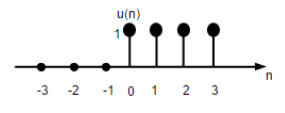
La figura anterior muestra la representación gráfica de una función de paso discreto.
Función de rampa de unidad
Una función de rampa de unidad discreta se puede definir como:
$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$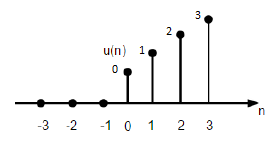
La figura dada arriba muestra la representación gráfica de una señal de rampa discreta.
Función parabólica
La función parabólica unitaria discreta se denota como p (n) y se puede definir como;
$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$En términos de función de paso unitario, se puede escribir como;
$$P(n) = \frac{n^{2}}{2}U(n)$$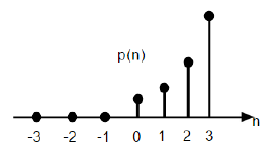
La figura dada arriba muestra la representación gráfica de una secuencia parabólica.
Señal sinusoidal
Todas las señales de tiempo continuo son periódicas. Las secuencias sinusoidales de tiempo discreto pueden ser periódicas o no. Dependen del valor de ω. Para que una señal de tiempo discreta sea periódica, la frecuencia angular ω debe ser un múltiplo racional de 2π.
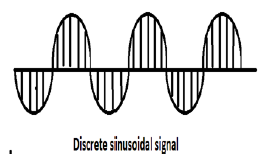
En la figura anterior se muestra una señal sinusoidal discreta.
La forma discreta de una señal sinusoidal se puede representar en el formato:
$$x(n) = A\sin(\omega n + \phi)$$Aquí A, ω y φ tienen su significado habitual y n es el número entero. El período de tiempo de la señal sinusoidal discreta viene dado por:
$$N =\frac{2\pi m}{\omega}$$Donde, N y m son números enteros.
Las señales de tiempo continuo se pueden clasificar de acuerdo con diferentes condiciones u operaciones realizadas en las señales.
Señales pares e impares
Incluso señal
Se dice que una señal es incluso si satisface la siguiente condición;
$$x(-t) = x(t)$$La inversión temporal de la señal no implica ningún cambio en la amplitud aquí. Por ejemplo, considere la onda triangular que se muestra a continuación.
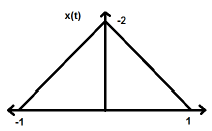
La señal triangular es una señal uniforme. Dado que es simétrico con respecto al eje Y. Podemos decir que es una imagen especular sobre el eje Y.
Considere otra señal como se muestra en la figura siguiente.
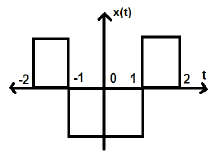
Podemos ver que la señal anterior es uniforme, ya que es simétrica con respecto al eje Y.
Señal extraña
Se dice que una señal es impar si cumple la siguiente condición
$$x(-t) = -x(t)$$Aquí, tanto la inversión del tiempo como el cambio de amplitud tienen lugar simultáneamente.
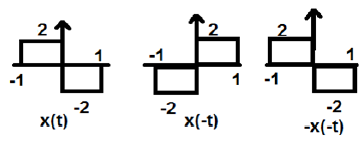
En la figura anterior, podemos ver una señal de paso x (t). Para probar si es una señal impar o no, primero hacemos la inversión de tiempo, es decir, x (-t) y el resultado es como se muestra en la figura. Luego invertimos la amplitud de la señal resultante, es decir, –x (-t) y obtenemos el resultado como se muestra en la figura.
Si comparamos la primera y la tercera forma de onda, podemos ver que son iguales, es decir, x (t) = -x (-t), lo que satisface nuestros criterios. Por lo tanto, la señal anterior es una señal impar.
A continuación se muestran algunos resultados importantes relacionados con señales pares e impares.
- Par × par = par
- Impar × Impar = Par
- Par × Impar = Impar
- Incluso ± Incluso = Incluso
- Impar ± Impar = Impar
- Even ± Odd = Ni par ni impar
Representación de cualquier señal en forma par o impar
Algunas señales no se pueden clasificar directamente en tipos pares o impares. Estos se representan como una combinación de señales pares e impares.
$$x(t)\rightarrow x_{e}(t)+x_{0}(t)$$Donde x e (t) representa la señal par y x o (t) representa la señal impar
$$x_{e}(t)=\frac{[x(t)+x(-t)]}{2}$$Y
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$Ejemplo
Encuentra las partes pares e impares de la señal. $x(n) = t+t^{2}+t^{3}$
Solution - De invertir x (n), obtenemos
$$x(-n) = -t+t^{2}-t^{3}$$
Ahora, según la fórmula, la parte par
$$x_{e}(t) = \frac{x(t)+x(-t)}{2}$$
$$= \frac{[(t+t^{2}+t^{3})+(-t+t^{2}-t^{3})]}{2}$$
$$= t^{2}$$
Del mismo modo, de acuerdo con la fórmula, la parte impar es
$$x_{0}(t)=\frac{[x(t)-x(-t)]}{2}$$
$$= \frac{[(t+t^{2}+t^{3})-(-t+t^{2}-t^{3})]}{2}$$
$$= t+t^{3}$$
Señales periódicas y no periódicas
Señales periódicas
La señal periódica se repite después de cierto intervalo de tiempo. Podemos mostrar esto en forma de ecuación como:
$$x(t) = x(t)\pm nT$$Donde, n = un número entero (1,2,3 ……)
T = Período de tiempo fundamental (FTP) ≠ 0 y ≠ ∞
El período de tiempo fundamental (FTP) es el valor de tiempo positivo y fijo más pequeño para el que la señal es periódica.
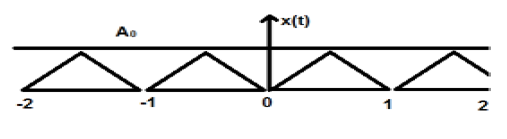
En la figura anterior se muestra una señal triangular de amplitud A. Aquí, la señal se repite cada 1 segundo. Por tanto, podemos decir que la señal es periódica y su FTP es de 1 seg.
Señal no periódica
Simplemente, podemos decir, las señales, que no son periódicas, son de naturaleza no periódica. Como es obvio, estas señales no se repetirán después de ningún intervalo de tiempo.
Las señales no periódicas no siguen un formato determinado; por lo tanto, ninguna ecuación matemática particular puede describirlos.
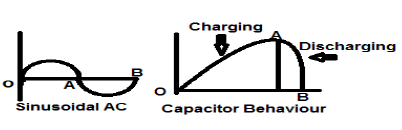
Señales de energía y potencia
Se dice que una señal es una señal de energía, si y solo si, la energía total contenida es finita y distinta de cero (0 <E <∞). Por lo tanto, para cualquier tipo de señal de energía, la señal normalizada total es finita y distinta de cero.
Una señal de corriente alterna sinusoidal es un ejemplo perfecto de señal de tipo Energía porque está en semiciclo positivo en un caso y luego es negativa en el siguiente semiciclo. Por tanto, su potencia media se vuelve cero.
Un capacitor sin pérdidas también es un ejemplo perfecto de señal de tipo Energía porque cuando está conectado a una fuente se carga hasta su nivel óptimo y cuando se quita la fuente, disipa esa cantidad igual de energía a través de una carga y hace que su potencia promedio sea cero.
Para cualquier señal finita x (t), la energía se puede simbolizar como E y se escribe como;
$$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$La densidad espectral de las señales de tipo de energía da la cantidad de energía distribuida en varios niveles de frecuencia.
Señales de tipo de potencia
Se dice que una señal es de tipo de potencia, si y sólo si, la potencia media normalizada es finita y distinta de cero, es decir (0 <p <∞). Para la señal de tipo de potencia, la potencia media normalizada es finita y distinta de cero. Casi todas las señales periódicas son señales de potencia y su potencia media es finita y distinta de cero.
En forma matemática, la potencia de una señal x (t) se puede escribir como;
$$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$Diferencia entre señales de energía y potencia
La siguiente tabla resume las diferencias de energía y señales de potencia.
| Señal de potencia | Señal de energía |
|---|---|
| Las señales periódicas prácticas son señales de potencia. | Las señales no periódicas son señales de energía. |
| Aquí, la potencia promedio normalizada es finita y distinta de cero. | Aquí, la energía total normalizada es finita y distinta de cero. |
| Matemáticamente, $$P = \lim_{T \rightarrow \infty}1/T\int_{-T/2}^{+T/2} x^{2}(t)dt$$ |
Matemáticamente, $$E = \int_{-\infty}^{+\infty} x^{2}(t)dt$$ |
| La existencia de estas señales es infinita en el tiempo. | Estas señales existen durante un período de tiempo limitado. |
| La energía de la señal de potencia es infinita durante un tiempo infinito. | La potencia de la señal de energía es cero durante un tiempo infinito. |
Ejemplos resueltos
Example 1 - Encuentra el poder de una señal $z(t) = 2\cos(3\Pi t+30^{o})+4\sin(3\Pi +30^{o})$
Solution- Las dos señales anteriores son ortogonales entre sí porque sus términos de frecuencia son idénticos entre sí y también tienen la misma diferencia de fase. Entonces, el poder total será la suma de los poderes individuales.
Dejar $z(t) = x(t)+y(t)$
Dónde $x(t) = 2\cos (3\Pi t+30^{o})$ y $y(t) = 4\sin(3\Pi +30^{o})$
El poder de $x(t) = \frac{2^{2}}{2} = 2$
El poder de $y(t) = \frac{4^{2}}{2} = 8$
Por lo tanto, $P(z) = p(x)+p(y) = 2+8 = 10$… Resp.
Example 2 - Prueba si la señal dada $x(t) = t^{2}+j\sin t$ es conjugado o no?
Solution- Aquí, la parte real que es t 2 es par y la parte impar (imaginaria) es$\sin t$es impar. Entonces la señal anterior es señal conjugada.
Example 3 - Verifique si $X(t)= \sin \omega t$ es una señal par o impar.
Solution - Dado $X(t) = \sin \omega t$
Al invertir el tiempo, obtendremos $\sin (-\omega t)$
Pero sabemos que $\sin(-\phi) = -\sin \phi$.
Por lo tanto,
$$\sin (-\omega t) = -\sin \omega t$$Esto satisface la condición para que una señal sea impar. Por lo tanto,$\sin \omega t$ es una señal extraña.
Al igual que las señales de tiempo continuo, las señales de tiempo discreto pueden clasificarse de acuerdo con las condiciones u operaciones de las señales.
Señales pares e impares
Incluso señal
Se dice que una señal es par o simétrica si satisface la siguiente condición;
$$x(-n) = x(n)$$
Aquí, podemos ver que x (-1) = x (1), x (-2) = x (2) y x (-n) = x (n). Por tanto, es una señal uniforme.
Señal extraña
Se dice que una señal es impar si satisface la siguiente condición;
$$x(-n) = -x(n)$$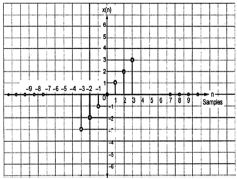
En la figura, podemos ver que x (1) = -x (-1), x (2) = -x (2) yx (n) = -x (-n). Por lo tanto, es una señal extraña y antisimétrica.
Señales periódicas y no periódicas
Una señal de tiempo discreta es periódica si y solo si, satisface la siguiente condición:
$$x(n+N) = x(n)$$Aquí, la señal x (n) se repite después de N período. Esto se puede entender mejor si se considera una señal de coseno:
$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$Para que la señal se vuelva periódica, debe cumplirse la siguiente condición;
$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$es decir $2\pi f_{0}N$ es un múltiplo integral de $2\pi$
$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$Las frecuencias de las señales sinusoidales discretas están separadas por un múltiplo integral de $2\pi$.
Señales de energía y potencia
Señal de energía
La energía de una señal de tiempo discreta se denota como E. Matemáticamente, se puede escribir como;
$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$Si cada valor individual de $x(n)$se elevan al cuadrado y se suman, obtenemos la señal de energía. aquí$x(n)$ es la señal de energía y su energía es finita en el tiempo, es decir, $ 0 <E <\ infty $
Señal de potencia
La potencia promedio de una señal discreta se representa como P. Matemáticamente, esto se puede escribir como;
$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$Aquí, la potencia es finita, es decir, 0 <P <∞. Sin embargo, hay algunas señales que no pertenecen ni a señales de tipo de energía ni de potencia.
Hay otras señales, que son el resultado de la operación realizada en ellas. Algunos tipos comunes de señales se describen a continuación.
Señales conjugadas
Señales, que satisface la condición. $x(t) = x*(-t)$ se llaman señales conjugadas.
Dejar $x(t) = a(t)+jb(t)$... eqn. 1
Entonces, $x(-t) = a(-t)+jb(-t)$
Y $x*(-t) = a(-t)-jb(-t)$... eqn. 2
Por condición, $x(t) = x*(-t)$
Si comparamos las ecuaciones derivadas 1 y 2, podemos ver que la parte real es par, mientras que la imaginaria es impar. Ésta es la condición para que una señal sea de tipo conjugado.
Señales antisimétricas conjugadas
Señales, que satisfacen la condición $x(t) = -x*(-t)$ se llaman señal antisimétrica conjugada
Dejar $x(t) = a(t)+jb(t)$... eqn. 1
Entonces $x(-t) = a(-t)+jb(-t)$
Y $x*(-t) = a(-t)-jb(-t)$
$-x*(-t) = -a(-t)+jb(-t)$... eqn. 2
Por condición $x(t) = -x*(-t)$
Ahora, compare de nuevo ambas ecuaciones tal como lo hicimos para las señales conjugadas. Aquí, encontraremos que la parte real es impar y la imaginaria es par. Esta es la condición para que una señal se convierta en un tipo antisimétrico conjugado.
Ejemplo
Deja que la señal dada sea $x(t) = \sin t+jt^{2}$.
Aquí, la parte real es $\sin t$ es extraño y la parte imaginaria es $t^2$incluso. Entonces, esta señal se puede clasificar como señal antisimétrica conjugada.
Cualquier función se puede dividir en dos partes. Una parte es simetría conjugada y la otra parte es antisimétrica conjugada. Entonces, cualquier señal x (t) se puede escribir como
$$x(t) = xcs(t)+xcas(t)$$Dónde $xcs(t)$ es una señal simétrica conjugada y $xcas(t)$ es señal anti-simétrica conjugada
$$xcs(t) = \frac{[x(t)+x*(-t)]}{2}$$Y
$$xcas(t) = \frac{[x(t)-x*(-t)]}{2}$$Señales simétricas de media onda
Cuando una señal satisface la condición $cx(t) = -x(t\pm (\frac{T_{0}}{2}))$, se llama señal simétrica de media onda. Aquí, la inversión de amplitud y el desplazamiento temporal de la señal tienen lugar a medio tiempo. Para la señal simétrica de media onda, el valor promedio será cero, pero este no es el caso cuando se invierte la situación.
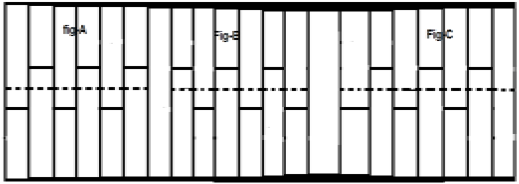
Considere una señal x (t) como se muestra en la figura A anterior. El primer paso es cambiar el tiempo de la señal y hacerla$x[t-(\frac{T}{2})]$. Entonces, la nueva señal se cambia como se muestra en la figura B. Luego, invertimos la amplitud de la señal, es decir, la hacemos$-x[t-(\frac{T}{2})]$ como se muestra en la figura C. Dado que esta señal se repite después de un cambio de medio tiempo y una inversión de amplitud, es una señal simétrica de media onda.
Señal ortogonal
Se dice que dos señales x (t) e y (t) son ortogonales si satisfacen las dos condiciones siguientes.
Condition 1 - $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [para señal no periódica]
Condition 2 - $\int x(t)y(t) = 0$ [Para señal periódica]
Las señales, que contienen armónicos impares (3 rd , 5 th , 7 th ... etc.) Y tienen diferentes frecuencias, son mutuamente ortogonales entre sí.
En las señales de tipo trigonométrico, las funciones seno y coseno también son ortogonales entre sí; siempre que tengan la misma frecuencia y estén en la misma fase. De la misma manera, las señales CC (señales de corriente continua) y sinusoidales también son ortogonales entre sí. Si x (t) y y (t) son dos señales ortogonales y$z(t) = x(t)+y(t)$ entonces la potencia y la energía de z (t) se pueden escribir como;
$$P(z) = p(x)+p(y)$$ $$E(z) = E(x)+E(y)$$Ejemplo
Analizar la señal: $z(t) = 3+4\sin(2\pi t+30^0)$
Aquí, la señal se compone de una señal de CC (3) y una función sinusoidal. Entonces, por propiedad, esta señal es una señal ortogonal y las dos sub-señales en ella son mutuamente ortogonales entre sí.
Desplazamiento significa movimiento de la señal, ya sea en el dominio del tiempo (alrededor del eje Y) o en el dominio de la amplitud (alrededor del eje X). En consecuencia, podemos clasificar el cambio en dos categorías denominadas Cambio de tiempo y Cambio de amplitud, que se analizan posteriormente a continuación.
Cambio de hora
Cambio de tiempo significa, cambio de señales en el dominio del tiempo. Matemáticamente, se puede escribir como
$$x(t) \rightarrow y(t+k)$$Este valor de K puede ser positivo o negativo. De acuerdo con el signo del valor k, tenemos dos tipos de cambios denominados Cambio a la derecha y Cambio a la izquierda.
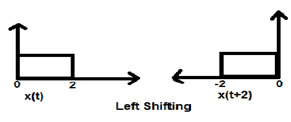
Caso 1 (K> 0)
Cuando K es mayor que cero, el desplazamiento de la señal tiene lugar hacia la "izquierda" en el dominio del tiempo. Por lo tanto, este tipo de cambio se conoce como cambio a la izquierda de la señal.
Example
Caso 2 (K <0)
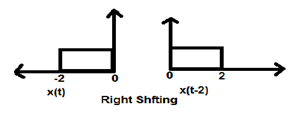
Cuando K es menor que cero, el desplazamiento de la señal tiene lugar hacia la derecha en el dominio del tiempo. Por lo tanto, este tipo de cambio se conoce como cambio a la derecha.
Example
La figura que se muestra a continuación muestra el desplazamiento a la derecha de una señal en 2.
Cambio de amplitud
El cambio de amplitud significa el cambio de señal en el dominio de amplitud (alrededor del eje X). Matemáticamente, se puede representar como:
$$x(t) \rightarrow x(t)+K$$Este valor de K puede ser positivo o negativo. En consecuencia, tenemos dos tipos de desplazamiento de amplitud que se comentan a continuación.
Caso 1 (K> 0)
Cuando K es mayor que cero, el desplazamiento de la señal tiene lugar hacia arriba en el eje x. Por lo tanto, este tipo de cambio se conoce como cambio ascendente.
Example
Consideremos una señal x (t) que se da como;
$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$Supongamos que K = + 1 para que la nueva señal se pueda escribir como -
$y(t) \rightarrow x(t)+1$ Entonces, y (t) finalmente se puede escribir como;
$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$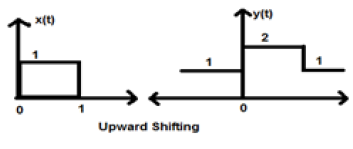
Caso 2 (K <0)
Cuando K es menor que cero, el desplazamiento de la señal tiene lugar hacia abajo en el eje X. Por lo tanto, se denomina desplazamiento de la señal hacia abajo.
Example
Consideremos una señal x (t) que se da como;
$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$Supongamos que K = -1 para que la nueva señal se pueda escribir como;
$y(t)\rightarrow x(t)-1$ Entonces, y (t) finalmente se puede escribir como;
$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$
El escalado de una señal significa que una constante se multiplica por el tiempo o la amplitud de la señal.
Escala de tiempo
Si una constante se multiplica por el eje de tiempo, se conoce como escala de tiempo. Esto se puede representar matemáticamente como;
$x(t) \rightarrow y(t) = x(\alpha t)$ o $x(\frac{t}{\alpha})$; donde α ≠ 0
Entonces, siendo el eje y el mismo, la magnitud del eje x disminuye o aumenta según el signo de la constante (ya sea positiva o negativa). Por lo tanto, la escala también se puede dividir en dos categorías, como se explica a continuación.
Compresión de tiempo
Siempre que alfa es mayor que cero, la amplitud de la señal se divide por alfa mientras que el valor del eje Y sigue siendo el mismo. Esto se conoce como compresión de tiempo.
Example
Consideremos una señal x (t), que se muestra como en la figura siguiente. Tomemos el valor de alfa como 2. Entonces, y (t) será x (2t), que se ilustra en la figura dada.

Claramente, podemos ver en las figuras anteriores que la magnitud del tiempo en el eje y permanece igual pero la amplitud en el eje x se reduce de 4 a 2. Por lo tanto, es un caso de compresión de tiempo.
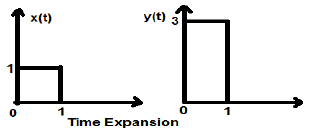
Expansión de tiempo
Cuando el tiempo se divide por la constante alfa, la magnitud del eje Y de la señal se multiplica por alfa, manteniendo la magnitud del eje X tal como está. Por lo tanto, esto se denomina señal de tipo expansión de tiempo.
Example
Consideremos una señal cuadrada x (t), de magnitud 1. Cuando la escalamos en el tiempo por una constante 3, tal que $x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$, entonces la amplitud de la señal se modifica 3 veces, como se muestra en la siguiente figura.
Escala de amplitud
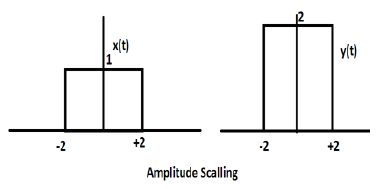
La multiplicación de una constante con la amplitud de la señal provoca un escalado de amplitud. Dependiendo del signo de la constante, puede ser una escala de amplitud o una atenuación. Consideremos una señal de onda cuadrada x (t) = Π (t / 4).
Supongamos que definimos otra función y (t) = 2 Π (t / 4). En este caso, el valor del eje y se duplicará, manteniendo el valor del eje de tiempo tal como está. El se ilustra en la figura que se muestra a continuación.
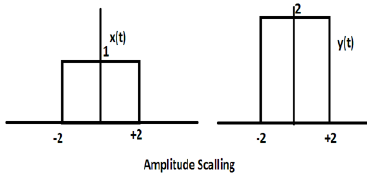
Considere otra función de onda cuadrada definida como z (t) donde z (t) = 0.5 Π (t / 4). Aquí, la amplitud de la función z (t) será la mitad de la de x (t), es decir, el eje de tiempo permanece igual, el eje de amplitud se reducirá a la mitad. Esto se ilustra en la figura que se muestra a continuación.
Siempre que el tiempo de una señal se multiplica por -1, la señal se invierte. Produce su imagen especular sobre el eje Y o X. Esto se conoce como inversión de la señal.
La inversión se puede clasificar en dos tipos según la condición de si el tiempo o la amplitud de la señal se multiplica por -1.
Inversión del tiempo
Siempre que el tiempo de la señal se multiplica por -1, se conoce como inversión de tiempo de la señal. En este caso, la señal produce su imagen especular sobre el eje Y. Matemáticamente, esto se puede escribir como;
$$x(t) \rightarrow y(t) \rightarrow x(-t)$$Esto se puede entender mejor con el siguiente ejemplo.

En el ejemplo anterior, podemos ver claramente que la señal se ha invertido alrededor de su eje Y. Por lo tanto, también es un tipo de escala de tiempo, pero aquí la cantidad de escala es (-1) siempre.
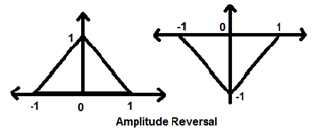
Inversión de amplitud
Siempre que la amplitud de una señal se multiplica por -1, se conoce como inversión de amplitud. En este caso, la señal produce su imagen especular sobre el eje X. Matemáticamente, esto se puede escribir como;
$$x(t)\rightarrow y(t)\rightarrow -x(t)$$Considere el siguiente ejemplo. La inversión de amplitud se puede ver claramente.
Dos operaciones muy importantes que se realizan en las señales son la diferenciación y la integración.
Diferenciación
La diferenciación de cualquier señal x (t) significa la representación en pendiente de esa señal con respecto al tiempo. Matemáticamente, se representa como;
$$x(t)\rightarrow \frac{dx(t)}{dt}$$En el caso de la diferenciación OPAMP, esta metodología es muy útil. Podemos diferenciar fácilmente una señal gráficamente en lugar de usar la fórmula. Sin embargo, la condición es que la señal debe ser de tipo rectangular o triangular, lo que ocurre en la mayoría de los casos.
| Señal original | Señal diferenciada |
|---|---|
| Rampa | Paso |
| Paso | Impulso |
| Impulso | 1 |
La tabla anterior ilustra la condición de la señal después de ser diferenciada. Por ejemplo, una señal de rampa se convierte en una señal de paso después de la diferenciación. De manera similar, una señal de paso unitario se convierte en una señal de impulso.
Ejemplo
Que la señal que se nos da sea $x(t) = 4[r(t)-r(t-2)]$. Cuando se traza esta señal, se verá como la del lado izquierdo de la figura que se muestra a continuación. Ahora, nuestro objetivo es diferenciar la señal dada.
Para empezar, comenzaremos a diferenciar la ecuación dada. Sabemos que la señal de rampa después de la diferenciación da una señal de paso unitario.
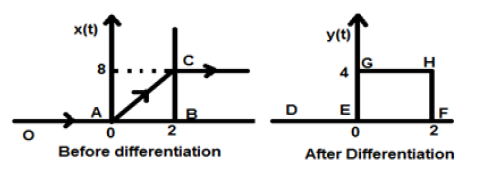
Entonces, nuestra señal resultante y (t) se puede escribir como;
$y(t) = \frac{dx(t)}{dt}$
$= \frac{d4[r(t)-r(t-2)]}{dt}$
$= 4[u(t)-u(t-2)]$
Ahora esta señal se traza finalmente, que se muestra en el lado derecho de la figura anterior.
La integración de cualquier señal significa la suma de esa señal en un dominio de tiempo particular para obtener una señal modificada. Matemáticamente, esto se puede representar como:
$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$Aquí también, en la mayoría de los casos, podemos hacer una integración matemática y encontrar la señal resultante, pero la integración directa en rápida sucesión es posible para las señales que se representan gráficamente en formato rectangular. Como diferenciación, aquí también nos referiremos a una tabla para obtener el resultado rápidamente.
| Señal original | Señal integrada |
|---|---|
| 1 | impulso |
| Impulso | paso |
| Paso | Rampa |
Ejemplo
Consideremos una señal $x(t) = u(t)-u(t-3)$. Se muestra en la Fig-1 a continuación. Claramente, podemos ver que es una señal de paso. Ahora lo integraremos. Con referencia a la tabla, sabemos que la integración de la señal de paso produce una señal de rampa.
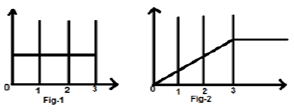
Sin embargo, lo calcularemos matemáticamente,
$y(t) = \int_{-\infty}^{t}x(t)dt$
$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$
$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$
$= r(t)-r(t-3)$
Lo mismo se traza como se muestra en la fig-2,
La convolución de dos señales en el dominio del tiempo es equivalente a la multiplicación de su representación en el dominio de la frecuencia. Matemáticamente, podemos escribir la convolución de dos señales como
$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$Pasos para la convolución
- Tome la señal x 1 (t) y coloque t = p allí para que sea x 1 (p).
- Tome la señal x 2 (t) y haga el paso 1 y hágalo x 2 (p).
- Realice el plegado de la señal, es decir, x 2 (-p).
- Hacer el cambio de tiempo de la señal anterior x 2 [- (pt)]
- Luego haz la multiplicación de ambas señales. es decir$x_{1}(p).x_{2}[−(p−t)]$
Ejemplo
Hagamos la convolución de una señal escalonada u (t) con su propia clase.
$y(t) = u(t)*u(t)$
$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$
Ahora bien, esta t puede ser mayor o menor que cero, que se muestran en las siguientes figuras
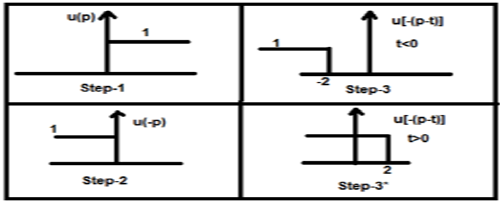
Entonces, con el caso anterior, el resultado surge con las siguientes posibilidades
$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$
$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$
Propiedades de la convolución
Conmutativo
Afirma que el orden de convolución no importa, lo que se puede mostrar matemáticamente como
$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$De asociación
Establece que el orden de convolución que involucra tres señales puede ser cualquier cosa. Matemáticamente, se puede mostrar como;
$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$Distributivo
Primero se pueden agregar dos señales y luego se puede hacer su convolución a la tercera señal. Esto es equivalente a la convolución de dos señales individualmente con la tercera señal y finalmente agregadas. Matemáticamente, esto se puede escribir como;
$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$Zona
Si una señal es el resultado de la convolución de dos señales, entonces el área de la señal es la multiplicación de esas señales individuales. Matemáticamente esto se puede escribir
Si $y(t) = x_{1}*x_{2}(t)$
Entonces, Área de y (t) = Área de x 1 (t) X Área de x 2 (t)
Escalada
Si dos señales se escalan a alguna constante desconocida "a" y se realiza la convolución, la señal resultante también se convolucionará a la misma constante "a" y se dividirá por esa cantidad como se muestra a continuación.
Si, $x_{1}(t)*x_{2}(t) = y(t)$
Luego, $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$
Retrasar
Suponga que una señal y (t) es el resultado de la convolución de dos señales x1 (t) y x2 (t). Si las dos señales se retrasan en el tiempo t1 y t2 respectivamente, la señal resultante y (t) se retrasará en (t1 + t2). Matemáticamente, se puede escribir como:
Si, $x_{1}(t)*x_{2}(t) = y(t)$
Luego, $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$
Ejemplos resueltos
Example 1 - Encuentre la convolución de las señales u (t-1) yu (t-2).
Solution- Las señales dadas son u (t-1) yu (t-2). Su convolución se puede hacer como se muestra a continuación:
$y(t) = u(t-1)*u(t-2)$
$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$
$= r(t-1)+r(t-2)$
$= r(t-3)$
Example 2 - Encuentra la convolución de dos señales dadas por
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$
Solution -
x 2 (n) se puede decodificar como$x_{2}(n) = \lbrace 2,2,2,2,2\rbrace Originalfirst$
x 1 (n) se da previamente$= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$
Similar, $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
Señal resultante,
$X(Z) = X_{1}(Z)X_{2}(z)$
$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$
Tomando la transformación Z inversa de lo anterior, obtendremos la señal resultante como
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ Origen al principio
Example 3 - Determine la convolución de las siguientes 2 señales -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
Tomando la transformación Z de las señales, obtenemos,
$x(z) = 2+2Z^{-1}+2Z^{-3}$
Y $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$
Ahora la convolución de dos señales significa la multiplicación de sus transformaciones Z
Es decir $Y(Z) = X(Z) \times h(Z)$
$= \lbrace 2+2Z^{-1}+2Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$
$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+3Z^{-5}+Z^{-6}\rbrace$
Tomando la transformación Z inversa, la señal resultante se puede escribir como;
$y(n) = \lbrace 2,5,8,6,6,1 \rbrace Originalfirst$
Algunos sistemas tienen retroalimentación y otros no. Aquellos que no tienen sistemas de retroalimentación, su salida depende solo de los valores actuales de la entrada. El valor pasado de los datos no está presente en ese momento. Estos tipos de sistemas se conocen como sistemas estáticos. Tampoco depende de valores futuros.
Dado que estos sistemas no tienen ningún registro pasado, tampoco tienen memoria. Por lo tanto, decimos que todos los sistemas estáticos son sistemas sin memoria. Tomemos un ejemplo para entender mucho mejor este concepto.
Ejemplo
Verifiquemos si los siguientes sistemas son estáticos o no.
- $y(t) = x(t)+x(t-1)$
- $y(t) = x(2t)$
- $y(t) = x = \sin [x(t)]$
un) $y(t) = x(t)+x(t-1)$
Aquí, x (t) es el valor actual. No tiene relación con los valores pasados de la época. Entonces, es un sistema estático. Sin embargo, en el caso de x (t-1), si ponemos t = 0, se reducirá ax (-1) que es un valor pasado dependiente. Entonces, no es estático. Por tanto, aquí y (t) no es un sistema estático.
segundo) $y(t) = x(2t)$
Si sustituimos t = 2, el resultado será y (t) = x (4). Nuevamente, depende del valor futuro. Entonces, tampoco es un sistema estático.
C) $y(t) = x = \sin [x(t)]$
En esta expresión, estamos tratando con la función seno. El rango de la función seno se encuentra entre -1 y +1. Entonces, sean cuales sean los valores que sustituyamos por x (t), obtendremos un valor entre -1 y +1. Por lo tanto, podemos decir que no depende de ningún valor pasado o futuro. Por tanto, es un sistema estático.
De los ejemplos anteriores, podemos sacar las siguientes conclusiones:
- Cualquier sistema que tenga cambios de tiempo no es estático.
- Cualquier sistema que tenga cambio de amplitud tampoco es estático.
- Los casos de integración y diferenciación tampoco son estáticos.
Si un sistema depende del valor pasado y futuro de la señal en cualquier momento del tiempo, se lo conoce como sistema dinámico. A diferencia de los sistemas estáticos, estos no son sistemas sin memoria. Almacenan valores pasados y futuros. Por tanto, requieren algo de memoria. Entendamos mejor esta teoría a través de algunos ejemplos.
Ejemplos
Descubra si los siguientes sistemas son dinámicos.
a) $y(t) = x(t+1)$
En este caso, si ponemos t = 1 en la ecuación, se convertirá a x (2), que es un valor dependiente futuro. Porque aquí damos entrada como 1 pero muestra el valor de x (2). Como es una señal dependiente del futuro, claramente es un sistema dinámico.
b) $y(t) = Real[x(t)]$
$$= \frac{[x(t)+x(t)^*]}{2}$$En este caso, cualquiera que sea el valor que pongamos, mostrará esa señal de valor real de tiempo. No depende de valores pasados o futuros. Por tanto, no es un sistema dinámico sino estático.
c) $y(t) = Even[x(t)]$
$$= \frac{[x(t)+x(-t)]}{2}$$Aquí, si sustituimos t = 1, una señal muestra x (1) y otra mostrará x (-1), que es un valor pasado. De manera similar, si ponemos t = -1, entonces una señal mostrará x (-1) y otra mostrará x (1), que es un valor futuro. Por tanto, claramente se trata de un caso de sistema dinámico.
d) $y(t) = \cos [x(t)]$
En este caso, como el sistema es función coseno, tiene un cierto dominio de valores que se encuentra entre -1 y +1. Por lo tanto, sean cuales sean los valores que pongamos, obtendremos el resultado dentro del límite especificado. Por tanto, es un sistema estático
De los ejemplos anteriores, podemos sacar las siguientes conclusiones:
- Todas las señales de casos de cambio de tiempo son señales dinámicas.
- También en el caso de escalado de tiempo, todas las señales son señales dinámicas.
- Las señales de los casos de integración son señales dinámicas.
Anteriormente, vimos que el sistema necesita ser independiente de los valores pasados y futuros para volverse estático. En este caso, la condición es casi la misma con pocas modificaciones. Aquí, para que el sistema sea causal, debe ser independiente de los valores futuros únicamente. Eso significa que la dependencia pasada no causará ningún problema para que el sistema se convierta en causal.
Los sistemas causales son sistemas realizables práctica o físicamente. Consideremos algunos ejemplos para entender esto mucho mejor.
Ejemplos
Consideremos las siguientes señales.
a) $y(t) = x(t)$
Aquí, la señal solo depende de los valores actuales de x. Por ejemplo, si sustituimos t = 3, el resultado se mostrará solo para ese instante de tiempo. Por lo tanto, como no depende del valor futuro, podemos llamarlo sistema Causal.
b) $y(t) = x(t-1)$
Aquí, el sistema depende de valores pasados. Por ejemplo, si sustituimos t = 3, la expresión se reducirá ax (2), que es un valor pasado frente a nuestra entrada. En ningún caso, depende de valores futuros. Por tanto, este sistema también es un sistema causal.
c) $y(t) = x(t)+x(t+1)$
En este caso, el sistema tiene dos partes. La parte x (t), como hemos discutido anteriormente, depende solo de los valores presentes. Entonces, no hay problema con eso. Sin embargo, si tomamos el caso de x (t + 1), claramente depende de los valores futuros porque si ponemos t = 1, la expresión se reducirá ax (2) que es el valor futuro. Por tanto, no es causal.
Un sistema no causal es exactamente opuesto al del sistema causal. Si un sistema depende de los valores futuros de la entrada en cualquier instante del tiempo, se dice que el sistema es un sistema no causal.
Ejemplos
Tomemos algunos ejemplos y tratemos de entender esto de una mejor manera.
a) $y(t) = x(t+1)$
Ya hemos discutido este sistema en el sistema causal también. Para cualquier entrada, reducirá el sistema a su valor futuro. Por ejemplo, si ponemos t = 2, se reducirá ax (3), que es un valor futuro. Por lo tanto, el sistema es No Causal.
b) $y(t) = x(t)+x(t+2)$
En este caso, x (t) es puramente una función dependiente del valor presente. Ya hemos discutido que la función x (t + 2) depende del futuro porque para t = 3 dará valores para x (5). Por tanto, no es causal.
c) $y(t) = x(t-1)+x(t)$
En este sistema, depende de los valores presentes y pasados de la entrada dada. Independientemente de los valores que sustituyamos, nunca mostrará ninguna dependencia futura. Claramente, no es un sistema no causal; más bien es un sistema causal.
Un sistema anti-causal es solo una versión ligeramente modificada de un sistema no causal. El sistema depende únicamente de los valores futuros de la entrada. No tiene dependencia ni de los valores presentes ni de los pasados.
Ejemplos
Descubra si los siguientes sistemas son anticausal.
a) $y(t) = x(t)+x(t-1)$
El sistema tiene dos subfunciones. Una subfunción x (t + 1) depende del valor futuro de la entrada, pero otra subfunción x (t) depende solo del presente. Como el sistema también depende del valor presente además del valor futuro, este sistema no es anti-causal.
b) $y(t) = x(t+3)$
Si analizamos el sistema anterior, podemos ver que el sistema depende solo de los valores futuros del sistema, es decir, si ponemos t = 0, se reducirá ax (3), que es un valor futuro. Este sistema es un ejemplo perfecto de sistema anti-causal.
Un sistema lineal sigue las leyes de superposición. Esta ley es condición necesaria y suficiente para probar la linealidad del sistema. Aparte de esto, el sistema es una combinación de dos tipos de leyes:
- Ley de aditividad
- Ley de homogeneidad

Tanto la ley de homogeneidad como la ley de aditividad se muestran en las figuras anteriores. Sin embargo, existen otras condiciones para comprobar si el sistema es lineal o no.
The conditions are -
- La salida debe ser cero para una entrada cero.
- No debe haber ningún operador no lineal presente en el sistema.
Ejemplos de operadores no lineales:
(a) Operadores trigonométricos: Sin, Cos, Tan, Cot, Sec, Cosec, etc.
(b) Exponencial, logarítmico, módulo, cuadrado, cubo, etc.
(c) sa (i / p), Sinc (i / p), Sqn (i / p), etc.
La entrada x o la salida y no deben tener estos operadores no lineales.
Ejemplos
Averigüemos si los siguientes sistemas son lineales.
a) $y(t) = x(t)+3$
Este sistema no es un sistema lineal porque viola la primera condición. Si ponemos la entrada como cero, haciendo x (t) = 0, entonces la salida no es cero.
b) $y(t) = \sin tx(t)$
En este sistema, si damos entrada como cero, la salida será cero. Por tanto, la primera condición se cumple claramente. Nuevamente, no hay un operador no lineal que se haya aplicado en x (t). Por tanto, también se cumple la segunda condición. Por tanto, el sistema es un sistema lineal.
c) $y(t) = \sin (x(t))$
En el sistema anterior, se satisface la primera condición porque si ponemos x (t) = 0, la salida también será sin (0) = 0. Sin embargo, la segunda condición no se cumple, ya que existe un operador no lineal que opera x (t). Por tanto, el sistema no es lineal.
Si queremos definir este sistema, podemos decir que los sistemas que no son lineales son sistemas no lineales. Claramente, todas las condiciones que se están violando en los sistemas lineales deben cumplirse en este caso.
Condiciones
La salida no debe ser cero cuando la entrada aplicada es cero.
Se puede aplicar cualquier operador no lineal en la entrada o en la salida para hacer que el sistema no sea lineal.
Ejemplos
Para saber si los sistemas dados son lineales o no lineales.
a) $y(t) = e^{x(t)}$
En el sistema anterior, la primera condición se satisface porque si hacemos que la entrada sea cero, la salida es 1. Además, se aplica un operador exponencial no lineal a la entrada. Claramente, es un caso de sistema no lineal.
b) $y(t) = x(t+1)+x(t-1)$
El tipo de sistema anterior se ocupa de valores pasados y futuros. Sin embargo, si hacemos que su entrada sea cero, entonces ninguno de sus valores existe. Por lo tanto, podemos decir que si la entrada es cero, entonces la versión de la entrada escalada en el tiempo y desplazada en el tiempo también será cero, lo que viola nuestra primera condición. Nuevamente, no hay un operador no lineal presente. Por tanto, también se infringe la segunda condición. Claramente, este sistema no es un sistema no lineal; más bien es un sistema lineal.
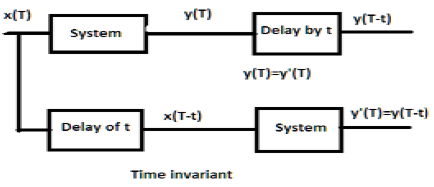
Para un sistema invariante en el tiempo, la salida y la entrada deben retrasarse en alguna unidad de tiempo. Cualquier retraso proporcionado en la entrada debe reflejarse en la salida para un sistema invariante en el tiempo.
Ejemplos
a) $y(T) = x(2T)$
Si la expresión anterior, primero pasa por el sistema y luego por el retardo de tiempo (como se muestra en la parte superior de la figura); entonces la salida se convertirá en$x(2T-2t)$. Ahora, la misma expresión pasa primero por un retardo de tiempo y luego por el sistema (como se muestra en la parte inferior de la figura). La salida se convertirá$x(2T-t)$.
Por tanto, el sistema no es invariante en el tiempo.
b) $y(T) = \sin [x(T)]$
Si la señal pasa primero a través del sistema y luego a través del proceso de retardo de tiempo, la salida será $\sin x(T-t)$. De manera similar, si el sistema pasa primero por el retardo de tiempo y luego a través del sistema, la salida será$\sin x(T-t)$. Podemos ver claramente que ambas salidas son iguales. Por tanto, el sistema es invariante en el tiempo.
Para un sistema de variación de tiempo, también, la salida y la entrada deben retrasarse por alguna constante de tiempo, pero el retraso en la entrada no debe reflejarse en la salida. Todos los casos de escalado de tiempo son ejemplos de sistema de variación de tiempo. De manera similar, cuando el coeficiente en la relación del sistema es una función del tiempo, entonces también el sistema es una variante del tiempo.
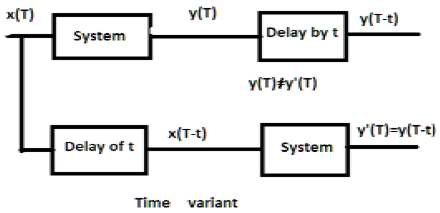
Ejemplos
a) $y(t) = x[\cos T]$
Si la señal anterior pasa primero a través del sistema y luego a través del retardo de tiempo, la salida será $x\cos (T-t)$. Si pasa primero por el retardo de tiempo y luego por el sistema, será$x(\cos T-t)$. Como las salidas no son las mismas, el sistema varía en el tiempo.
b) $y(T) = \cos T.x(T)$
Si la expresión anterior pasa primero a través del sistema y luego a través del retardo de tiempo, entonces la salida será $\cos(T-t)x(T-t)$. Sin embargo, si la expresión pasa primero por el retardo de tiempo y luego por el sistema, la salida será$\cos T.x(T-t)$. Como las salidas no son las mismas, claramente el sistema varía con el tiempo.
Un sistema estable satisface la condición BIBO (entrada acotada para salida acotada). Aquí, acotado significa finito en amplitud. Para un sistema estable, la salida debe ser acotada o finita, para entrada finita o acotada, en cada instante de tiempo.
Algunos ejemplos de entradas acotadas son funciones de seno, coseno, CC, signo y paso unitario.
Ejemplos
a) $y(t) = x(t)+10$
Aquí, para una entrada acotada definida, podemos obtener una salida acotada definida, es decir, si ponemos $x(t) = 2, y(t) = 12$que está delimitado por la naturaleza. Por tanto, el sistema es estable.
b) $y(t) = \sin [x(t)]$
En la expresión dada, sabemos que las funciones seno tienen un límite definido de valores, que se encuentra entre -1 y +1. Entonces, cualesquiera que sean los valores que sustituyamos en x (t), obtendremos los valores dentro de nuestro límite. Por tanto, el sistema es estable.
Los sistemas inestables no satisfacen las condiciones BIBO. Por lo tanto, para una entrada acotada, no podemos esperar una salida acotada en caso de sistemas inestables.
Ejemplos
a) $y(t) = tx(t)$
Aquí, para una entrada finita, no podemos esperar una salida finita. Por ejemplo, si ponemos$x(t) = 2 \Rightarrow y(t) = 2t$. Este no es un valor finito porque no conocemos el valor de t. Por lo tanto, se puede variar desde cualquier lugar. Por tanto, este sistema no es estable. Es un sistema inestable.
b) $y(t) = \frac{x(t)}{\sin t}$
Hemos comentado anteriormente que la función seno tiene un rango definido de -1 a +1; pero aquí está presente en el denominador. Entonces, en el peor de los casos, si ponemos t = 0 y la función seno se vuelve cero, todo el sistema tenderá al infinito. Por tanto, este tipo de sistema no es nada estable. Obviamente, este es un sistema inestable.
Example 1 - Compruebe si $y(t) = x*(t)$ es lineal o no lineal.
Solution- La función representa el conjugado de entrada. Puede ser verificado por la primera ley de homogeneidad y la ley de aditividad o por las dos reglas. Sin embargo, la verificación a través de las reglas es mucho más fácil, así que lo seguiremos.
Si la entrada al sistema es cero, la salida también tiende a cero. Por lo tanto, nuestra primera condición está satisfecha. No se utiliza un operador no lineal ni en la entrada ni en la salida. Por tanto, el sistema es lineal.
Example 2 - Compruebe si $y(t)=\begin{cases}x(t+1), & t > 0\\x(t-1), & t\leq 0\end{cases}$ es lineal o no lineal
Solution- Claramente, podemos ver que cuando el tiempo se vuelve menor o igual a cero, la entrada se vuelve cero. Entonces, podemos decir que con una entrada cero, la salida también es cero y nuestra primera condición se cumple.
Nuevamente, no se utiliza un operador no lineal en la entrada ni en la salida. Por tanto, el sistema es lineal.
Example 3 - Compruebe si $y(t) = \sin t.x(t)$ es estable o no.
Solution - Supongamos que hemos tomado el valor de x (t) como 3. Aquí, la función seno se ha multiplicado con ella y el valor máximo y mínimo de la función seno varía entre -1 y +1.
Por tanto, el valor máximo y mínimo de toda la función también variará entre -3 y +3. Por lo tanto, el sistema es estable porque aquí estamos obteniendo una entrada acotada para una salida acotada.
La Transformada de Fourier de Tiempo Discreto (DTFT) existe para señales de energía y potencia. La transformación Z tampoco existe para señales de tipo energía ni potencia (NENP), hasta cierto punto solo. El reemplazo$z=e^{jw}$ se utiliza para la conversión de transformada Z a DTFT solo para señales absolutamente sumables.
Entonces, la transformada Z de la señal de tiempo discreta x (n) en una serie de potencias se puede escribir como:
$$X(z) = \sum_{n-\infty}^\infty x(n)Z^{-n}$$La ecuación anterior representa una ecuación de transformada Z de dos lados.
Generalmente, cuando una señal se transforma en Z, se puede representar como:
$$X(Z) = Z[x(n)]$$O $x(n) \longleftrightarrow X(Z)$
Si es una señal de tiempo continua, entonces las transformadas Z no son necesarias porque se utilizan transformaciones de Laplace. Sin embargo, las señales de tiempo discreto solo se pueden analizar mediante transformaciones Z.
Región de convergencia
La región de convergencia es el rango de la variable compleja Z en el plano Z. La transformación Z de la señal es finita o convergente. Entonces, ROC representa el conjunto de valores de Z, para los cuales X (Z) tiene un valor finito.
Propiedades de ROC
- ROC no incluye ningún poste.
- Para la señal del lado derecho, ROC estará fuera del círculo en el plano Z.
- Para la señal del lado izquierdo, ROC estará dentro del círculo en el plano Z.
- Para la estabilidad, ROC incluye círculo unitario en el plano Z.
- Para la señal de ambos lados, ROC es un anillo en el plano Z.
- Para la señal de duración finita, ROC es el plano Z completo.
La transformación Z se caracteriza únicamente por:
- Expresión de X (Z)
- ROC de X (Z)
Señales y su ROC
| x (n) | X (Z) | República de China |
|---|---|---|
| $\delta(n)$ | $1$ | Plano Z completo |
| $U(n)$ | $1/(1-Z^{-1})$ | Mod (Z)> 1 |
| $a^nu(n)$ | $1/(1-aZ^{-1})$ | Mod (Z)> Mod (a) |
| $-a^nu(-n-1)$ | $1/(1-aZ^{-1})$ | Mod (Z) <Mod (a) |
| $na^nu(n)$ | $aZ^{-1}/(1-aZ^{-1})^2$ | Mod (Z)> Mod (a) |
| $-a^nu(-n-1)$ | $aZ^{-1}/(1-aZ^{-1})^2$ | Mod (Z) <Mod (a) |
| $U(n)\cos \omega n$ | $(Z^2-Z\cos \omega)/(Z^2-2Z \cos \omega +1)$ | Mod (Z)> 1 |
| $U(n)\sin \omega n$ | $(Z\sin \omega)/(Z^2-2Z \cos \omega +1)$ | Mod (Z)> 1 |
Ejemplo
Encontremos la transformada Z y la ROC de una señal dada como $x(n) = \lbrace 7,3,4,9,5\rbrace$, donde el origen de la serie está en 3.
Solution - Aplicando la fórmula que tenemos -
$X(z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-1}^3 x(n)Z^{-n}$
$= x(-1)Z+x(0)+x(1)Z^{-1}+x(2)Z^{-2}+x(3)Z^{-3}$
$= 7Z+3+4Z^{-1}+9Z^{-2}+5Z^{-3}$
ROC es el plano Z completo excluyendo Z = 0, ∞, -∞
En este capítulo, comprenderemos las propiedades básicas de las transformadas Z.
Linealidad
Establece que cuando dos o más señales discretas individuales se multiplican por constantes, sus respectivas transformadas Z también se multiplicarán por las mismas constantes.
Matemáticamente,
$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$Proof - Lo sabemos,
$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$
$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= a_1X_1(z)+a_2X_2(z)$ (Por lo tanto probado)
Aquí, la República de China es $ROC_1\bigcap ROC_2$.
Cambio de hora
La propiedad de desplazamiento de tiempo describe cómo el cambio en el dominio del tiempo en la señal discreta afectará el dominio Z, que se puede escribir como;
$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$O $x(n-1)\longleftrightarrow Z^{-1}X(Z)$
Proof -
Dejar $y(P) = X(P-K)$
$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$
$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$
Sea s = pk
$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$
$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$
$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$
$= Z^{-k}X(Z)$ (Por lo tanto probado)
Aquí, ROC se puede escribir como Z = 0 (p> 0) o Z = ∞ (p <0)
Ejemplo
U (n) y U (n-1) se pueden representar de la siguiente manera
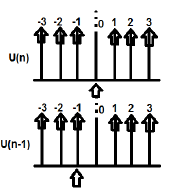
La transformación Z de U (n) cab se escribe como;
$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$
La transformación Z de U (n-1) se puede escribir como;
$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$
Asi que aqui $x(n-n_0) = Z^{-n_0}X(Z)$ (Por lo tanto probado)
Escala de tiempo
La propiedad Time Scaling nos dice cuál será el dominio Z de la señal cuando el tiempo se escale en su forma discreta, que se puede escribir como;
$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$Proof -
Dejar $y(p) = a^{p}x(p)$
$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$
$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$
$= X(a^{-1}Z)$(Por lo tanto probado)
ROC: = Mod (ar1) <Mod (Z) <Mod (ar2) donde Mod = Modulus
Ejemplo
Determinemos la transformación Z de $x(n) = a^n \cos \omega n$ utilizando la propiedad de escala de tiempo.
Solution -
Ya sabemos que la transformación Z de la señal $\cos (\omega n)$ está dado por -
$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$
Ahora, aplicando la propiedad de escala de tiempo, la transformación Z de $a^n \cos \omega n$ Se puede escribir como;
$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$
$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$
$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$
Diferenciación sucesiva
La propiedad de diferenciación sucesiva muestra que la transformación Z tendrá lugar cuando diferenciamos la señal discreta en el dominio del tiempo, con respecto al tiempo. Esto se muestra a continuación.
$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$Proof -
Considere el LHS de la ecuación: $\frac{dx(n)}{dn}$
$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$$= x(n)-X(n-1)$
$= x(Z)-Z^{-1}x(Z)$
$= (1-Z^{-1})x(Z)$ (Por lo tanto probado)
ROC: R1 <Mod (Z) <R2
Ejemplo
Encontremos la transformada Z de una señal dada por $x(n) = n^2u(n)$
Por propiedad podemos escribir
$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$
$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$
$= Z/((Z-1)^2$
$= y(let)$
Ahora, Z [ny] se puede averiguar aplicando nuevamente la propiedad,
$Z(n,y) = -Z\frac{dy}{dz}$
$= -Z\frac{d[Z/(Z-1)^3]}{dz}$
$= Z(Z+1)/(Z-1)^2$
Circunvolución
Esto representa el cambio en el dominio Z del sistema cuando tiene lugar una convolución en la forma de señal discreta, que se puede escribir como -
$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$
Proof -
$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$
$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$
$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$
Sea nk = l, entonces la ecuación anterior cab se escribe como -
$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$
$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$
$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$
$= X_1(Z).X_2(Z)$ (Por lo tanto probado)
República de China:$ROC\bigcap ROC2$
Ejemplo
Encontremos la convolución dada por dos señales.
$x_1(n) = \lbrace 3,-2,2\rbrace$ ... (ecuación 1)
$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ... (ecuación 2)
La transformación Z de la primera ecuación se puede escribir como;
$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$
$= 3-2Z^{-1}+2Z^{-2}$
La transformación Z de la segunda señal se puede escribir como;
$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$
$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
Entonces, la convolución de las dos señales anteriores está dada por:
$X(Z) = [x_1(Z)^*x_2(Z)]$
$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$
Tomando la transformación Z inversa obtenemos,
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$
Teorema del valor inicial
Si x (n) es una secuencia causal, que tiene su transformación Z como X (z), entonces el teorema del valor inicial se puede escribir como;
$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$
Proof - Lo sabemos,
$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$
Ampliando la serie anterior, obtenemos;
$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$
En el caso anterior, si Z → ∞ entonces $Z^{-n}\rightarrow 0$ (Porque n> 0)
Por lo tanto, podemos decir;
$\lim_{z \to \infty}X(z) = X(0)$ (Por lo tanto probado)
Teorema del valor final
El Teorema del valor final establece que si la transformada Z de una señal se representa como X (Z) y los polos están todos dentro del círculo, entonces su valor final se denota como x (n) o X (∞) y se puede escribir como -
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$
Conditions -
- Es aplicable solo para sistemas causales.
- $X(Z)(1-Z^{-1})$ debe tener polos dentro del círculo unitario en el plano Z.
Proof - sabemos que
$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$
$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$
$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$
Aquí, podemos aplicar la propiedad avanzada de transformación Z unilateral. Entonces, la ecuación anterior se puede reescribir como;
$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$
Ahora poniendo z = 1 en la ecuación anterior, podemos expandir la ecuación anterior -
$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$
Esto se puede formular como;
$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(Por lo tanto probado)
Ejemplo
Encontremos el valor inicial y final de x (n) cuya señal está dada por
$X(Z) = 2+3Z^{-1}+4Z^{-2}$
Solution - Primero, encontremos el valor inicial de la señal aplicando el teorema
$x(0) = \lim_{z \to \infty}X(Z)$
$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$
$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$
Ahora encontremos el valor final de la señal aplicando el teorema
$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$
$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$
$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$
$= 2+1+1-4 = 0$
Some other properties of Z-transform are listed below -
Diferenciación en frecuencia
Da el cambio en el dominio Z de la señal, cuando su señal discreta se diferencia con respecto al tiempo.
$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$
Su ROC se puede escribir como;
$r_2< Mod(Z)< r_1$
Ejemplo
Encontremos el valor de x (n) mediante Diferenciación en frecuencia, cuya señal discreta en el dominio Z está dada por $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$
Por propiedad, podemos escribir que
$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$
$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$
$= (aZ^{-1})/(1+aZ^{-1})$
$= 1-1/(1+aZ^{-1})$
$nx(n) = \delta(n)-(-a)^nu(n)$
$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$
Multiplicación en el tiempo
Da el cambio en el dominio Z de la señal cuando la multiplicación tiene lugar a un nivel de señal discreto.
$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$
Conjugación en el tiempo
Esto representa la representación de una señal discreta conjugada en el dominio Z.
$X^*(n)\longleftrightarrow X^*(Z^*)$
Un sistema, que tiene una función de sistema, solo puede ser estable si todos los polos se encuentran dentro del círculo unitario. Primero, verificamos si el sistema es causal o no. Si el sistema es Causal, entonces buscamos su determinación de estabilidad BIBO; donde la estabilidad BIBO se refiere a la entrada acotada para la condición de salida acotada.
Esto se puede escribir como;
$Mod(X(Z))< \infty$
$= Mod(\sum x(n)Z^{-n})< \infty$
$= \sum Mod(x(n)Z^{-n})< \infty$
$= \sum Mod[x(n)(re^{jw})^{-n}]< 0$
$= \sum Mod[x(n)r^{-n}]Mod[e^{-jwn}]< \infty$
$= \sum_{n = -\infty}^\infty Mod[x(n)r^{-n}]< \infty$
La ecuación anterior muestra la condición de existencia de la transformada Z.
Sin embargo, la condición para la existencia de la señal DTFT es
$$\sum_{n = -\infty}^\infty Mod(x(n)< \infty$$Ejemplo 1
Intentemos encontrar la transformada Z de la señal, que se da como
$x(n) = -(-0.5)^{-n}u(-n)+3^nu(n)$
$= -(-2)^nu(n)+3^nu(n)$
Solution - Aquí, para $-(-2)^nu(n)$ la ROC es del lado izquierdo y Z <2
por $3^nu(n)$ ROC está del lado derecho y Z> 3
Por tanto, aquí la transformada Z de la señal no existirá porque no hay una región común.
Ejemplo 2
Intentemos averiguar la transformada Z de la señal dada por
$x(n) = -2^nu(-n-1)+(0.5)^nu(n)$
Solution - Aquí, para $-2^nu(-n-1)$ ROC de la señal es del lado izquierdo y Z <2
Para señal $(0.5)^nu(n)$ ROC es del lado derecho y Z> 0.5
Entonces, la ROC común se forma como 0.5 <Z <2
Por lo tanto, la transformada Z se puede escribir como;
$X(Z) = \lbrace\frac{1}{1-2Z^{-1}}\rbrace+\lbrace\frac{1}{(1-0.5Z)^{-1}}\rbrace$
Ejemplo 3
Intentemos encontrar la transformada Z de la señal, que se da como $x(n) = 2^{r(n)}$
Solution- r (n) es la señal de rampa. Entonces la señal se puede escribir como;
$x(n) = 2^{nu(n)}\lbrace 1, n<0 (u(n)=0)\quad and\quad2^n, n\geq 0(u(n) = 1)\rbrace$
$= u(-n-1)+2^nu(n)$
Aquí, por la señal $u(-n-1)$ y ROC Z <1 y para $2^nu(n)$ con ROC es Z> 2.
Entonces, la transformación Z de la señal no existirá.
Transformación Z para sistema causal
El sistema causal se puede definir como $h(n) = 0,n<0$. Para el sistema causal, ROC estará fuera del círculo en el plano Z.
$H(Z) = \displaystyle\sum\limits_{n = 0}^{\infty}h(n)Z^{-n}$
Ampliando la ecuación anterior,
$H(Z) = h(0)+h(1)Z^{-1}+h(2)Z^{-2}+...\quad...\quad...$
$= N(Z)/D(Z)$
Para los sistemas causales, la expansión de la función de transferencia no incluye las potencias positivas de Z. Para el sistema causal, el orden del numerador no puede exceder el orden del denominador. Esto se puede escribir como-
$\lim_{z \rightarrow \infty}H(Z) = h(0) = 0\quad or\quad Finite$
Para la estabilidad del sistema causal, los polos de la función de transferencia deben estar dentro del círculo unitario en el plano Z.
Transformada Z para el sistema anti-causal
El sistema anticausal se puede definir como $h(n) = 0, n\geq 0$. Para el sistema anti-causal, los polos de la función de transferencia deben estar fuera del círculo unitario en el plano Z. Para el sistema anti-causal, ROC estará dentro del círculo en el plano Z.
Si queremos analizar un sistema, que ya está representado en el dominio de la frecuencia, como una señal de tiempo discreta, optamos por la transformación Z inversa.
Matemáticamente, se puede representar como;
$$x(n) = Z^{-1}X(Z)$$donde x (n) es la señal en el dominio del tiempo y X (Z) es la señal en el dominio de la frecuencia.
Si queremos representar la ecuación anterior en formato integral, podemos escribirla como
$$x(n) = (\frac{1}{2\Pi j})\oint X(Z)Z^{-1}dz$$Aquí, la integral está sobre una ruta cerrada C. Esta ruta está dentro de la ROC de x (z) y contiene el origen.
Métodos para encontrar la transformación Z inversa
Cuando se necesita el análisis en formato discreto, convertimos la señal de dominio de frecuencia de nuevo a formato discreto a través de la transformación Z inversa. Seguimos las siguientes cuatro formas de determinar la transformación Z inversa.
- Método de división larga
- Método de expansión de fracción parcial
- Método integral de residuos o contorno
Método de división larga
En este método, la transformada Z de la señal x (z) se puede representar como la relación del polinomio como se muestra a continuación;
$$x(z)=N(Z)/D(Z)$$Ahora, si seguimos dividiendo el numerador por el denominador, obtendremos una serie como se muestra a continuación.
$$X(z) = x(0)+x(1)Z^{-1}+x(2)Z^{-2}+...\quad...\quad...$$La secuencia anterior representa la serie de transformada Z inversa de la señal dada (para n≥0) y el sistema anterior es causal.
Sin embargo, para n <0, la serie se puede escribir como;
$$x(z) = x(-1)Z^1+x(-2)Z^2+x(-3)Z^3+...\quad...\quad...$$Método de expansión de fracción parcial
Aquí también la señal se expresa primero en forma N (z) / D (z).
Si es una fracción racional, se representará de la siguiente manera;
$x(z) = b_0+b_1Z^{-1}+b_2Z^{-2}+...\quad...\quad...+b_mZ^{-m})/(a_0+a_1Z^{-1}+a_2Z^{-2}+...\quad...\quad...+a_nZ^{-N})$
El anterior es incorrecto cuando m <ny an ≠ 0
Si la proporción no es la adecuada (es decir, incorrecta), entonces tenemos que convertirla a la forma adecuada para resolverla.
Método integral de residuos o contorno
En este método, obtenemos la transformada Z inversa x (n) sumando residuos de $[x(z)Z^{n-1}]$en todos los polos. Matemáticamente, esto puede expresarse como
$$x(n) = \displaystyle\sum\limits_{all\quad poles\quad X(z)}residues\quad of[x(z)Z^{n-1}]$$Aquí, el residuo de cualquier polo de orden m en $z = \beta$ es
$$Residues = \frac{1}{(m-1)!}\lim_{Z \rightarrow \beta}\lbrace \frac{d^{m-1}}{dZ^{m-1}}\lbrace (z-\beta)^mX(z)Z^{n-1}\rbrace$$Ejemplo 1
Encuentra la respuesta del sistema $s(n+2)-3s(n+1)+2s(n) = \delta (n)$, cuando todas las condiciones iniciales son cero.
Solution - Tomando la transformada Z en ambos lados de la ecuación anterior, obtenemos
$$S(z)Z^2-3S(z)Z^1+2S(z) = 1$$$\Rightarrow S(z)\lbrace Z^2-3Z+2\rbrace = 1$
$\Rightarrow S(z) = \frac{1}{\lbrace z^2-3z+2\rbrace}=\frac{1}{(z-2)(z-1)} = \frac{\alpha _1}{z-2}+\frac{\alpha _2}{z-1}$
$\Rightarrow S(z) = \frac{1}{z-2}-\frac{1}{z-1}$
Tomando la transformada Z inversa de la ecuación anterior, obtenemos
$S(n) = Z^{-1}[\frac{1}{Z-2}]-Z^{-1}[\frac{1}{Z-1}]$
$= 2^{n-1}-1^{n-1} = -1+2^{n-1}$
Ejemplo 2
Encuentre la función del sistema H (z) y la respuesta de la muestra unitaria h (n) del sistema cuya ecuación en diferencia se describe como en
$y(n) = \frac{1}{2}y(n-1)+2x(n)$
donde, y (n) y x (n) son la salida y la entrada del sistema, respectivamente.
Solution - Tomando la transformada Z de la ecuación en diferencias anterior, obtenemos
$y(z) = \frac{1}{2}Z^{-1}Y(Z)+2X(z)$
$= Y(Z)[1-\frac{1}{2}Z^{-1}] = 2X(Z)$
$= H(Z) = \frac{Y(Z)}{X(Z)} = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$
Este sistema tiene un poste en $Z = \frac{1}{2}$ y $Z = 0$ y $H(Z) = \frac{2}{[1-\frac{1}{2}Z^{-1}]}$
Por lo tanto, tomando la transformada Z inversa de lo anterior, obtenemos
$h(n) = 2(\frac{1}{2})^nU(n)$
Ejemplo 3
Determine Y (z), n≥0 en el siguiente caso:
$y(n)+\frac{1}{2}y(n-1)-\frac{1}{4}y(n-2) = 0\quad given\quad y(-1) = y(-2) = 1$
Solution - Aplicando la transformada Z a la ecuación anterior, obtenemos
$Y(Z)+\frac{1}{2}[Z^{-1}Y(Z)+Y(-1)]-\frac{1}{4}[Z^{-2}Y(Z)+Z^{-1}Y(-1)+4(-2)] = 0$
$\Rightarrow Y(Z)+\frac{1}{2Z}Y(Z)+\frac{1}{2}-\frac{1}{4Z^2}Y(Z)-\frac{1}{4Z}-\frac{1}{4} = 0$
$\Rightarrow Y(Z)[1+\frac{1}{2Z}-\frac{1}{4Z^2}] =\frac{1}{4Z}-\frac{1}{2}$
$\Rightarrow Y(Z)[\frac{4Z^2+2Z-1}{4Z^2}] = \frac{1-2Z}{4Z}$
$\Rightarrow Y(Z) = \frac{Z(1-2Z)}{4Z^2+2Z-1}$
Al igual que la transformada de Fourier de la señal de tiempo continuo, la transformada de Fourier de tiempo discreto se puede utilizar para representar una secuencia discreta en su representación de dominio de frecuencia equivalente y un sistema de tiempo discreto LTI y desarrollar varios algoritmos computacionales.
X (jω) en FT continua, es una función continua de x (n). Sin embargo, DFT se ocupa de representar x (n) con muestras de su espectro X (ω). Por lo tanto, esta herramienta matemática tiene mucha importancia computacional en una representación conveniente. Con esta herramienta se pueden procesar tanto secuencias periódicas como no periódicas. Las secuencias periódicas deben muestrearse extendiendo el período hasta el infinito.
Muestreo de dominio de frecuencia
De la introducción, está claro que necesitamos saber cómo proceder a través del muestreo en el dominio de la frecuencia, es decir, el muestreo X (ω). Por tanto, la relación entre la transformada de Fourier muestreada y la DFT se establece de la siguiente manera.
De manera similar, las secuencias periódicas pueden adaptarse a esta herramienta al extender el período N hasta el infinito.
Sea una secuencia no periódica, $X(n) = \lim_{N \to \infty}x_N(n)$
Definiendo su transformada de Fourier,
$X(\omega ) = \sum_{n=-\infty}^\infty x(n)e^{-jwn}X(K\delta \omega)$
Aquí, X (ω) se muestrea periódicamente, en cada intervalo de δω radianes.
Como X (ω) es periódico en 2π radianes, requerimos muestras solo en el rango fundamental. Las muestras se toman después de intervalos equidistantes en el rango de frecuencia 0≤ω≤2π. El espaciado entre intervalos equivalentes es$\delta \omega = \frac{2\pi }{N}k$ radián.
Ahora evaluando, $\omega = \frac{2\pi}{N}k$
$X(\frac{2\pi}{N}k) = \sum_{n = -\infty}^\infty x(n)e^{-j2\pi nk/N},$ ... eq (2)
donde k = 0,1, …… N-1
Después de subdividir lo anterior e intercambiar el orden de suma
$X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}[\displaystyle\sum\limits_{l = -\infty}^\infty x(n-Nl)]e^{-j2\pi nk/N}$ ... eq (3)
$\sum_{l=-\infty}^\infty x(n-Nl) = x_p(n) = a\quad periodic\quad function\quad of\quad period\quad N\quad and\quad its\quad fourier\quad series\quad = \sum_{k = 0}^{N-1}C_ke^{j2\pi nk/N}$
donde, n = 0,1,… .., N-1; 'p' - significa entidad o función periódica
Los coeficientes de Fourier son,
$C_k = \frac{1}{N}\sum_{n = 0}^{N-1}x_p(n)e^{-j2\pi nk/N}$k = 0,1,…, N-1 ... eq (4)
Comparando las ecuaciones 3 y 4, obtenemos;
$NC_k = X(\frac{2\pi}{N}k)$k = 0,1,…, N-1 ... eq (5)
$NC_k = X(\frac{2\pi}{N}k) = X(e^{jw}) = \displaystyle\sum\limits_{n = -\infty}^\infty x_p(n)e^{-j2\pi nk/N}$... eq (6)
De la expansión de la serie Fourier,
$x_p(n) = \frac{1}{N}\displaystyle\sum\limits_{k = 0}^{N-1}NC_ke^{j2\pi nk/N} = \frac{1}{N}\sum_{k = 0}^{N-1}X(\frac{2\pi}{N}k)e^{j2\pi nk/N}$... eq (7)
Donde n = 0,1,…, N-1
Aquí, obtuvimos la señal periódica de X (ω). $x(n)$ se puede extraer de $x_p(n)$ solo, si no hay alias en el dominio del tiempo. $N\geq L$
N = período de $x_p(n)$ L = período de $x(n)$
$x(n) = \begin{cases}x_p(n), & 0\leq n\leq N-1\\0, & Otherwise\end{cases}$
El mapeo se logra de esta manera.
Propiedades de DFT
Linealidad
Establece que la DFT de una combinación de señales es igual a la suma de DFT de señales individuales. Tomemos dos señales x 1 (n) y x 2 (n), cuyas DFT son X 1 (ω) y X 2 (ω) respectivamente. Así que si
$x_1(n)\rightarrow X_1(\omega)$y$x_2(n)\rightarrow X_2(\omega)$
Luego $ax_1(n)+bx_2(n)\rightarrow aX_1(\omega)+bX_2(\omega)$
dónde a y b son constantes.
Simetría
Las propiedades de simetría de DFT se pueden derivar de una manera similar a como obtuvimos las propiedades de simetría de DTFT. Sabemos que la DFT de la secuencia x (n) se denota por X (K). Ahora, si x (n) y X (K) son una secuencia de valores complejos, entonces se puede representar como en
$x(n) = x_R(n)+jx_1(n),0\leq n\leq N-1$
Y $X(K) = X_R(K)+jX_1(K),0\leq K\leq N-1$
Propiedad de dualidad
Consideremos una señal x (n), cuya DFT se expresa como X (K). Sea X (N) la secuencia de duración finita. Entonces, de acuerdo con el teorema de dualidad,
Si, $x(n)\longleftrightarrow X(K)$
Luego, $X(N)\longleftrightarrow Nx[((-k))_N]$
Entonces, al usar este teorema si conocemos la DFT, podemos encontrar fácilmente la secuencia de duración finita.
Propiedades conjugadas complejas
Supongamos que hay una señal x (n), cuya DFT también la conocemos como X (K). Ahora, si el conjugado complejo de la señal se da como x * (n), entonces podemos encontrar fácilmente la DFT sin hacer mucho cálculo usando el teorema que se muestra a continuación.
Si, $x(n)\longleftrightarrow X(K)$
Luego, $x*(n)\longleftrightarrow X*((K))_N = X*(N-K)$
Cambio de frecuencia circular
La multiplicación de la secuencia x (n) con la secuencia exponencial compleja $e^{j2\Pi kn/N}$es equivalente al desplazamiento circular de la DFT en L unidades de frecuencia. Ésta es la propiedad de desplazamiento temporal dual de la circular.
Si, $x(n)\longleftrightarrow X(K)$
Luego, $x(n)e^{j2\Pi Kn/N}\longleftrightarrow X((K-L))_N$
Multiplicación de dos secuencias
Si hay dos señales x 1 (n) y x 2 (n) y sus respectivas DFT son X 1 (k) y X 2 (K), entonces la multiplicación de señales en la secuencia de tiempo corresponde a la convolución circular de sus DFT.
Si, $x_1(n)\longleftrightarrow X_1(K)\quad\&\quad x_2(n)\longleftrightarrow X_2(K)$
Luego, $x_1(n)\times x_2(n)\longleftrightarrow X_1(K)© X_2(K)$
Teorema de Parseval
Para secuencias de valores complejos x (n) y y (n), en general
Si, $x(n)\longleftrightarrow X(K)\quad \&\quad y(n)\longleftrightarrow Y(K)$
Luego, $\sum_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\sum_{k = 0}^{N-1}X(K)Y^*(K)$
Sabemos que cuando $\omega = 2\pi K/N$ y $N\rightarrow \infty,\omega$ se convierte en una variable continua y la suma de límites se convierte $-\infty$ a $+\infty$.
Por lo tanto,
$$NC_k = X(\frac{2\pi}{N}k) = X(e^{j\omega}) = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{\frac{-j2\pi nk}{N}} = \displaystyle\sum\limits_{n = -\infty}^\infty x(n)e^{-j\omega n}$$Transformada de Fourier de tiempo discreto (DTFT)
Lo sabemos, $X(e^{j\omega}) = \sum_{n = -\infty}^\infty x(n)e^{-j\omega n}$
Dónde, $X(e^{j\omega})$es continuo y periódico en ω y con período 2π. … Eq (1)
Ahora,
$x_p(n) = \sum_{k = 0}^{N-1}NC_ke^{j2 \pi nk/N}$ … De la serie Fourier
$x_p(n) = \frac{1}{2\pi}\sum_{k=0}^{N-1}NC_ke^{j2\pi nk/N}\times \frac{2\pi}{N}$
ω se vuelve continuo y $\frac{2\pi}{N}\rightarrow d\omega$, por las razones antes citadas.
$x(n) = \frac{1}{2\pi}\int_{n = 0}^{2\pi}X(e^{j\omega})e^{j\omega n}d\omega$… Eq (2)
Transformada de Fourier de tiempo discreto inverso
Simbólicamente,
$x(n)\Longleftrightarrow x(e^{j\omega})$(El par de transformadas de Fourier)
Condición necesaria y suficiente para la existencia de la transformada de Fourier de tiempo discreto para una secuencia no periódica x (n) es sumable absoluta.
es decir$\sum_{n = -\infty}^\infty|x(n)|<\infty$
Propiedades de DTFT
Linearity : $a_1x_1(n)+a_2x_2(n)\Leftrightarrow a_1X_1(e^{j\omega})+a_2X_2(e^{j\omega})$
Time shifting - $x(n-k)\Leftrightarrow e^{-j\omega k}.X(e^{j\omega})$
Time Reversal - $x(-n)\Leftrightarrow X(e^{-j\omega})$
Frequency shifting - $e^{j\omega _0n}x(n)\Leftrightarrow X(e^{j(\omega -\omega _0)})$
Differentiation frequency domain - $nx(n) = j\frac{d}{d\omega}X(e^{j\omega})$
Convolution - $x_1(n)*x_2(n)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Multiplication - $x_1(n)\times x_2(n)\Leftrightarrow X_1(e^{j\omega})*X_2(e^{j\omega})$
Co-relation - $y_{x_1\times x_2}(l)\Leftrightarrow X_1(e^{j\omega})\times X_2(e^{j\omega})$
Modulation theorem - $x(n)\cos \omega _0n = \frac{1}{2}[X_1(e^{j(\omega +\omega _0})*X_2(e^{jw})$
Symmetry -$x^*(n)\Leftrightarrow X^*(e^{-j\omega})$ ;
$x^*(-n)\Leftrightarrow X^*(e^{j\omega})$ ;
$Real[x(n)]\Leftrightarrow X_{even}(e^{j\omega})$ ;
$Imag[x(n)]\Leftrightarrow X_{odd}(e^{j\omega})$ ;
$x_{even}(n)\Leftrightarrow Real[x(e^{j\omega})]$ ;
$x_{odd}(n)\Leftrightarrow Imag[x(e^{j\omega})]$ ;
Parseval’s theorem - $\sum_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$
Anteriormente, estudiamos el muestreo en el dominio de la frecuencia. Con ese conocimiento básico, probamos$X(e^{j\omega})$en el dominio de la frecuencia, de modo que se pueda realizar un análisis digital conveniente a partir de los datos muestreados. Por tanto, la DFT se muestrea tanto en el dominio del tiempo como en el de la frecuencia. Con la suposición$x(n) = x_p(n)$
Por lo tanto, DFT viene dada por:
$X(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{-\frac{j2\pi nk}{N}}$, k = 0,1,…., N − 1 … eq (3)
Y IDFT viene dado por -
$X(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k)e^{\frac{j2\pi nk}{N}}$, n = 0,1,…., N − 1 … eq (4)
$\therefore x(n)\Leftrightarrow X(k)$
Factor Twiddle
Se denota como $W_N$ y definido como $W_N = e^{-j2\pi /N}$. Su magnitud se mantiene siempre en la unidad. Fase de$W_N = -2\pi /N$. Es un vector en el círculo unitario y se utiliza por conveniencia computacional. Matemáticamente, se puede mostrar como:
$W_N^r = W_N^{r\pm N} = W_N^{r\pm 2N} = ...$
Es función de r y del período N.
Considere N = 8, r = 0,1,2,3,… .14,15,16,….
$\Longleftrightarrow W_8^0 = W_8^8 = W_8^{16} = ... = ... = W_8^{32} = ... =1= 1\angle 0$
$W_8^1 = W_8^9 = W_8^{17} = ... = ... = W_8^{33} = ... =\frac{1}{\sqrt 2}= j\frac{1}{\sqrt 2} = 1\angle-\frac{\pi}{4}$
Transformación lineal
Entendamos la Transformación Lineal -
Lo sabemos,
$DFT(k) = DFT[x(n)] = X(\frac{2\pi}{N}k) = \sum_{n = 0}^{N-1}x(n).W_n^{-nk};\quad k = 0,1,….,N−1$
$x(n) = IDFT[X(k)] = \frac{1}{N}\sum_{k = 0}^{N-1}X(k).W_N^{-nk};\quad n = 0,1,….,N−1$
Note- El cálculo de DFT se puede realizar con multiplicación compleja N 2 y suma compleja N (N-1).
$x_N = \begin{bmatrix}x(0)\\x(1)\\.\\.\\x(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad x_N$
$X_N = \begin{bmatrix}X(0)\\X(1)\\.\\.\\X(N-1) \end{bmatrix}\quad N\quad point\quad vector\quad of\quad signal\quad X_N$
$\begin{bmatrix}1 & 1 & 1 & ... & ... & 1\\1 & W_N & W_N^2 & ... & ... & W_N^{N-1}\\. & W_N^2 & W_N^4 & ... & ... & W_N^{2(N-1)}\\.\\1 & W_N^{N-1} & W_N^{2(N-1)} & ... & ... & W_N^{(N-1)(N-1)} \end{bmatrix}$
N - punto DFT en término de matriz está dado por - $X_N = W_Nx_N$
$W_N\longmapsto$ Matriz de transformación lineal
$Now,\quad x_N = W_N^{-1}X_N$
IDFT en forma de matriz está dada por
$$x_N = \frac{1}{N}W_N^*X_N$$Comparando ambas expresiones de $x_N,\quad W_N^{-1} = \frac{1}{N}W_N^*$ y $W_N\times W_N^* = N[I]_{N\times N}$
Por lo tanto, $W_N$ es una matriz de transformación lineal, una matriz ortogonal (unitaria).
De propiedad periódica de $W_N$ y de su propiedad simétrica, se puede concluir que, $W_N^{k+N/2} = -W_N^k$
Simetría circular
La DFT de N puntos de una duración finita x (n) de longitud N≤L, es equivalente a la DFT de N puntos de la extensión periódica de x (n), es decir $x_p(n)$ del período N. y $x_p(n) = \sum_{l = -\infty}^\infty x(n-Nl)$. Ahora, si desplazamos la secuencia, que es una secuencia periódica en k unidades hacia la derecha, se obtiene otra secuencia periódica. Esto se conoce como desplazamiento circular y viene dado por,
$$x_p^\prime (n) = x_p(n-k) = \sum_{l = -\infty}^\infty x(n-k-Nl)$$La nueva secuencia finita se puede representar como
$$x_p^\prime (n) = \begin{cases}x_p^\prime(n), & 0\leq n\leq N-1\\0 & Otherwise\end{cases}$$Example - Sea x (n) = {1,2,4,3}, N = 4,
$x_p^\prime (n) = x(n-k,modulo\quad N)\equiv x((n-k))_N\quad;ex-if\quad k=2i.e\quad 2\quad unit\quad right\quad shift\quad and\quad N = 4,$
Se asume que la dirección en el sentido de las agujas del reloj es una dirección positiva.
Tenemos, $x\prime(n) = x((n-2))_4$
$x\prime(0) = x((-2))_4 = x(2) = 4$
$x\prime(1) = x((-1))_4 = x(3) = 3$
$x\prime(2) = x((-2))_4 = x(0) = 1$
$x\prime(3) = x((1))_4 = x(1) = 2$
Conclusion - El desplazamiento circular de la secuencia de N puntos equivale a un desplazamiento lineal de su extensión periódica y viceversa.
Secuencia circularmente uniforme - $x(N-n) = x(n),\quad 1\leq n\leq N-1$
$i.e.x_p(n) = x_p(-n) = x_p(N-n)$
Conjugar incluso -$x_p(n) = x_p^*(N-n)$
Secuencia circularmente impar - $x(N-n) = -x(n),\quad 1\leq n\leq N-1$
$i.e.x_p(n) = -x_p(-n) = -x_p(N-n)$
Conjugado impar - $x_p(n) = -x_p^*(N-n)$
Ahora, $x_p(n) = x_{pe}+x_{po}(n)$, dónde,
$x_{pe}(n) = \frac{1}{2}[x_p(n)+x_p^*(N-n)]$
$x_{po}(n) = \frac{1}{2}[x_p(n)-x_p^*(N-n)]$
Para cualquier señal real x (n),$X(k) = X^*(N-k)$
$X_R(k) = X_R(N-k)$
$X_l(k) = -X_l(N-k)$
$\angle X(k) = -\angle X(N-K)$
Time reversal- muestra inversa sobre la 0ª muestra. Esto se da como;
$x((-n))_N = x(N-n),\quad 0\leq n\leq N-1$
La inversión de tiempo consiste en graficar muestras de secuencia, en el sentido de las agujas del reloj, es decir, en la dirección negativa asumida.
Algunas otras propiedades importantes
Otras propiedades importantes de IDFT $x(n)\longleftrightarrow X(k)$
Time reversal - $x((-n))_N = x(N-n)\longleftrightarrow X((-k))_N = X(N-k)$
Circular time shift - $x((n-l))_N \longleftrightarrow X(k)e^{j2\pi lk/N}$
Circular frequency shift - $x(n)e^{j2\pi ln/N} \longleftrightarrow X((k-l))_N$
Complex conjugate properties -
$x^*(n)\longleftrightarrow X^*((-k))_N = X^*(N-k)\quad and$
$x^*((-n))_N = x^*(N-n)\longleftrightarrow X^*(-k)$
Multiplication of two sequence -
$x_1(n)\longleftrightarrow X_1(k)\quad and\quad x_2(n)\longleftrightarrow X_2(k)$
$\therefore x_1(n)x_2(n)\longleftrightarrow X_1(k)\quadⓃ X_2(k)$
Circular convolution - y multiplicación de dos DFT
$x_1(k)\quad Ⓝ x_2(k) =\sum_{k = 0}^{N-1}x_1(n).x_2((m-n))_n,\quad m = 0,1,2,... .,N-1 $
$x_1(k)\quad Ⓝ x_2(k)\longleftrightarrow X_1(k).X_2(k)$
Circular correlation - si $x(n)\longleftrightarrow X(k)$ y $y(n)\longleftrightarrow Y(k)$ , entonces existe una secuencia de correlación cruzada denotada como $\bar Y_{xy}$ tal que $\bar Y_{xy}(l) = \sum_{n = 0}^{N-1}x(n)y^*((n-l))_N = X(k).Y^*(k)$
Parseval’s Theorem - si $x(n)\longleftrightarrow X(k)$ y $y(n)\longleftrightarrow Y(k)$;
$\displaystyle\sum\limits_{n = 0}^{N-1}x(n)y^*(n) = \frac{1}{N}\displaystyle\sum\limits_{n =0}^{N-1}X(k).Y^*(k)$
Tomemos dos secuencias de duración finita x 1 (n) y x 2 (n), que tienen una longitud entera como N. Sus DFT son X 1 (K) y X 2 (K) respectivamente, que se muestra a continuación:
$$X_1(K) = \sum_{n = 0}^{N-1}x_1(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$ $$X_2(K) = \sum_{n = 0}^{N-1}x_2(n)e^{\frac{j2\Pi kn}{N}}\quad k = 0,1,2...N-1$$Ahora, intentaremos encontrar la DFT de otra secuencia x 3 (n), que se da como X 3 (K)
$X_3(K) = X_1(K)\times X_2(K)$
Al tomar la IDFT de lo anterior obtenemos
$x_3(n) = \frac{1}{N}\displaystyle\sum\limits_{n = 0}^{N-1}X_3(K)e^{\frac{j2\Pi kn}{N}}$
Después de resolver la ecuación anterior, finalmente, obtenemos
$x_3(n) = \displaystyle\sum\limits_{m = 0}^{N-1}x_1(m)x_2[((n-m))_N]\quad m = 0,1,2...N-1$
| Puntos de comparación | Convolución lineal | Convolución circular |
|---|---|---|
| Cambiando | Desplazamiento lineal | Desplazamiento circular |
| Muestras en el resultado de convolución | $N_1+N_2−1$ | $Max(N_1,N_2)$ |
| Encontrar la respuesta de un filtro | Posible | Posible con relleno de cero |
Métodos de convolución circular
Generalmente, hay dos métodos, que se adoptan para realizar la convolución circular y son:
- Método de círculo concéntrico,
- Método de multiplicación de matrices.
Método del círculo concéntrico
Dejar $x_1(n)$ y $x_2(n)$ser dos secuencias dadas. Los pasos seguidos para la convolución circular de$x_1(n)$ y $x_2(n)$ son
Toma dos círculos concéntricos. Trazar N muestras de$x_1(n)$ sobre la circunferencia del círculo exterior (manteniendo la misma distancia puntos sucesivos) en sentido antihorario.
Para trazar $x_2(n)$, grafica N muestras de $x_2(n)$en el sentido de las agujas del reloj en el círculo interior, la muestra inicial se coloca en el mismo punto que la muestra 0 de$x_1(n)$
Multiplique las muestras correspondientes en los dos círculos y agréguelos para obtener el resultado.
Gire el círculo interior en sentido antihorario con una muestra a la vez.
Método de multiplicación de matrices
El método de matriz representa las dos secuencias dadas $x_1(n)$ y $x_2(n)$ en forma de matriz.
Una de las secuencias dadas se repite mediante el desplazamiento circular de una muestra a la vez para formar una matriz NXN.
La otra secuencia se representa como matriz de columnas.
La multiplicación de dos matrices da como resultado una convolución circular.
DFT proporciona un enfoque alternativo a la convolución en el dominio del tiempo. Se puede utilizar para realizar un filtrado lineal en el dominio de la frecuencia.
Así,$Y(\omega) = X(\omega).H(\omega)\longleftrightarrow y(n)$.
El problema en este enfoque en el dominio de la frecuencia es que $Y(\omega)$, $X(\omega)$ y $H(\omega)$son función continua de ω, lo que no es fructífero para la computación digital en computadoras. Sin embargo, DFT proporciona una versión muestreada de estas formas de onda para resolver el propósito.
La ventaja es que, teniendo conocimiento de técnicas de DFT más rápidas como FFT, se puede desarrollar un algoritmo computacionalmente más eficiente para la computación digital en comparación con el enfoque en el dominio del tiempo.
Considere una secuencia de duración finita, $[x(n) = 0,\quad for,n<0\quad and\quad n\geq L]$ (ecuación generalizada), excita un filtro lineal con respuesta de impulso $[h(n) = 0,\quad forn<0\quad and\quad n\geq M]$.
$$x(n)y(n)$$ $$output = y(n) = \sum_{k = 0}^{M-1}h(k).x(n-k)$$A partir del análisis de convolución, está claro que la duración de y (n) es L + M − 1.
En el dominio de la frecuencia,
$$Y(\omega) = X(\omega).H(\omega)$$Ahora, $Y(\omega)$ es una función continua de ω y se muestrea en un conjunto de frecuencias discretas con un número de muestras distintas que debe ser igual o superior a $L+M-1$.
$$DFT\quad size = N\geq L+M-1$$Con $\omega = \frac{2\pi}{N}k$,
$Y(\omega) = X(k).H(k)$, donde k = 0,1,…., N-1
Donde, X (k) y H (k) son DFT de N puntos de x (n) y h (n) respectivamente. $x(n)\& h(n)$ se rellenan con ceros hasta la longitud N. No distorsionará los espectros continuos $X(\omega)$ y $H(\omega)$. Ya que$N\geq L+M-1$, La DFT de N puntos de la secuencia de salida y (n) es suficiente para representar y (n) en el dominio de la frecuencia y estos hechos infieren que la multiplicación de las DFT de N puntos de X (k) y H (k), seguida del cálculo de IDFT de N puntos debe producir y (n).
Esto implica que la convolución circular de N puntos de x (n) y H (n) con relleno de ceros, equivale a la convolución lineal de x (n) y h (n).
Por tanto, DFT se puede utilizar para filtrado lineal.
Caution - N siempre debe ser mayor o igual que $L+M-1$. De lo contrario, el efecto de alias corrompería la secuencia de salida.
Suponga que la secuencia de entrada x (n) de larga duración debe procesarse con un sistema que tiene una respuesta de impulso de duración finita convolucionando las dos secuencias. Dado que el filtrado lineal realizado mediante DFT implica la operación en un bloque de datos de tamaño fijo, la secuencia de entrada se divide en diferentes bloques de datos de tamaño fijo antes del procesamiento.
Luego, los bloques sucesivos se procesan uno a la vez y los resultados se combinan para producir el resultado neto.
Como la convolución se realiza dividiendo la secuencia de entrada larga en diferentes secciones de tamaño fijo, se denomina convolución seccionada. Una secuencia de entrada larga se segmenta en bloques de tamaño fijo, antes del procesamiento del filtro FIR.
Se utilizan dos métodos para evaluar la convolución discreta:
Overlap-save method
Overlap-add method
Método de guardado superpuesto
Overlap-save es el nombre tradicional de una forma eficiente de evaluar la convolución discreta entre una señal muy larga x (n) y un filtro de respuesta de impulso finito (FIR) h (n). A continuación se muestran los pasos del método de guardado de superposición:
Sea la longitud del bloque de datos de entrada = N = L + M-1. Por lo tanto, longitud de DFT e IDFT = N. Cada bloque de datos lleva M-1 puntos de datos del bloque anterior seguidos de L nuevos puntos de datos para formar una secuencia de datos de longitud N = L + M-1.
Primero, se calcula la DFT de N puntos para cada bloque de datos.
Añadiendo ceros (L-1), la respuesta al impulso del filtro FIR aumenta en longitud y se calcula y almacena la DFT de N puntos.
Multiplicación de dos DFT de N puntos H (k) y X m (k): Y ′ m (k) = H (k) .X m (k), donde K = 0,1,2,… N-1
Entonces, IDFT [Y ′ m ((k)] = y ′ ((n) = [y ′ m (0), y ′ m (1), y ′ m (2), ....... y ' m (m-1), y' m (m), ....... y ' m (N-1)]
(aquí, N-1 = L + M-2)
Los primeros puntos M-1 se corrompen debido al aliasing y, por lo tanto, se descartan porque el registro de datos tiene una longitud N.
Los últimos L puntos son exactamente iguales como resultado de la convolución, por lo que
y ′ m (n) = y m (n) donde n = M, M + 1,… .N-1
Para evitar el aliasing, los últimos elementos M-1 de cada registro de datos se guardan y estos puntos se trasladan al registro posterior y se convierten en primeros elementos M-1.

El resultado de IDFT, donde se evitan los primeros puntos M-1, para anular el aliasing y los puntos L restantes constituyen el resultado deseado como el de una convolución lineal.
Método de adición de superposición
A continuación se muestran los pasos para encontrar la convolución discreta utilizando el método de superposición:
Deje que el tamaño del bloque de datos de entrada sea L. Por lo tanto, el tamaño de DFT e IDFT: N = L + M-1
Cada bloque de datos se agrega con ceros M-1 al último.
Calcule la DFT de N puntos.

Se multiplican dos DFT de N puntos: Y m (k) = H (k) .X m (k), donde k = 0,, 1,2,…., N-1
IDFT [Y m (k)] produce bloques de longitud N que no se ven afectados por el aliasing, ya que el tamaño de DFT es N = L + M-1 y aumenta la longitud de las secuencias a N puntos añadiendo ceros M-1 a cada uno. bloquear.
Los últimos puntos M-1 de cada bloque deben superponerse y agregarse a los primeros puntos M-1 del bloque siguiente.
(motivo: cada bloque de datos termina con ceros M-1)
Por lo tanto, este método se conoce como método Overlap-add. Por lo tanto, obtenemos ...
y (n) = {y 1 (0), y 1 (1), y 1 (2), ... .., y 1 (L-1), y 1 (L) + y 2 (0), y 1 (L + 1) + y 2 (1), ... ... .., y 1 (N-1) + y 2 (M-1), y 2 (M), ... .. . ... ... ...}
DCT (Transformada de coseno discreta) es una secuencia de N entradas x (n), 0≤n≤N-1, como una transformación lineal o combinación de exponenciales complejas. Como resultado, los coeficientes DFT son, en general, complejos incluso si x (n) es real.
Supongamos que intentamos encontrar una transformación ortogonal que tiene una estructura N × N que expresa una secuencia real x (n) como una combinación lineal de secuencia de coseno. Ya lo sabemos
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$
Y $x(n) = \frac{1}{N}\sum_{k = 0}^{N-1}x(k)cos\frac{2\Pi kn}{N}0\leq k \leq N-1$
Esto es posible si la secuencia de N puntos x (n) es real y par. Así,$x(n) = x(N-n),0\leq n \leq (N-1)$. La DFT resultante en sí misma es real y uniforme. Estas cosas dejan en claro que posiblemente podríamos diseñar una transformada de coseno discreta, para cualquier secuencia real de N puntos tomando la DFT de 2N puntos de una “extensión uniforme” de secuencia.
DCT se utiliza, básicamente, en el procesamiento de imágenes y voz. También se utiliza en la compresión de imágenes y señales de voz.
$DFT[s(n)] = S(k) = \sum_{n = 0}^{2N-1}s(n)W_{2N}^{nk},\quad where\quad 0\leq k \leq 2N-1$
$S(k) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)W_{2N}^{nk}+\displaystyle\sum\limits_{n = N}^{2N-1}x(2N-n-1)W_{2N}^{nk};\quad where\quad 0\leq k\leq 2N-1$
$\Rightarrow S(k) = W_{2N}^{-k/2}+\sum_{n = 0}^{N-1}x(n) [W_{2N}^{nk}W_{2N}^{k/2}+W_{2N}^{-nk}W_{2N}^{-k/2}];\quad where\quad 0\leq k\leq 2N-1$
$\Rightarrow S(k) = W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{N}(n+\frac{1}{2})k];\quad where\quad 0\leq k\leq 2N-1$
DCT se define por,
$V(k) = 2\sum_{n = 0}^{N-1}x(n)\cos [\frac{\pi}{2}(n+\frac{1}{2})k]\quad where\quad 0\leq k\leq N-1$
$\Rightarrow V(k) = W_{2N}^{\frac{k}{2}}S(k)\quad or\quad S(k) = W_{2N}^{\frac{k}{2}}V(k),\quad where\quad 0\leq k\leq N-1$
$\Rightarrow V(k) = 2R[W_{2N}^{\frac{k}{2}}\sum_{n = 0}^{N-1}x(n)W_{2N}^{nk}],\quad where\quad 0\leq k\leq N-1$
Ejemplo 1
Verificar el teorema de la secuencia de Parseval $x(n) = \frac{1^n}{4}u(n)$
Solution - $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X_1(e^{j\omega})|^2d\omega$
LHS $\displaystyle\sum\limits_{-\infty}^\infty|x_1(n)|^2$
$= \displaystyle\sum\limits_{-\infty}^{\infty}x(n)x^*(n)$
$= \displaystyle\sum\limits_{-\infty}^\infty(\frac{1}{4})^{2n}u(n) = \frac{1}{1-\frac{1}{16}} = \frac{16}{15}$
RHS $X(e^{j\omega}) = \frac{1}{1-\frac{1}{4}e-j\omega} = \frac{1}{1-0.25\cos \omega+j0.25\sin \omega}$
$\Longleftrightarrow X^*(e^{j\omega}) = \frac{1}{1-0.25\cos \omega-j0.25\sin \omega}$
Calculador, $X(e^{j\omega}).X^*(e^{j\omega})$
$= \frac{1}{(1-0.25\cos \omega)^2+(0.25\sin \omega)^2} = \frac{1}{1.0625-0.5\cos \omega}$
$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega$
$\frac{1}{2\pi}\int_{-\pi}^{\pi}\frac{1}{1.0625-0.5\cos \omega}d\omega = 16/15$
Podemos ver eso, LHS = RHS. (Por lo tanto probado)
Ejemplo 2
Calcule la DFT de N puntos de $x(n) = 3\delta (n)$
Solution - Lo sabemos,
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$
$= \displaystyle\sum\limits_{n = 0}^{N-1}3\delta(n)e^{\frac{j2\Pi kn}{N}}$
$ = 3\delta (0)\times e^0 = 1$
Entonces,$x(k) = 3,0\leq k\leq N-1$… Resp.
Ejemplo 3
Calcule la DFT de N puntos de $x(n) = 7(n-n_0)$
Solution - Lo sabemos,
$X(K) = \displaystyle\sum\limits_{n = 0}^{N-1}x(n)e^{\frac{j2\Pi kn}{N}}$
Sustituyendo el valor de x (n),
$\displaystyle\sum\limits_{n = 0}^{N-1}7\delta (n-n_0)e^{-\frac{j2\Pi kn}{N}}$
$= e^{-kj14\Pi kn_0/N}$… Ans
En métodos DFT anteriores, hemos visto que la parte computacional es demasiado larga. Queremos reducir eso. Esto se puede hacer mediante FFT o transformada rápida de Fourier. Entonces, podemos decir que FFT no es más que el cálculo de la transformada discreta de Fourier en un formato algorítmico, donde la parte computacional se reducirá.
La principal ventaja de tener FFT es que a través de ella podemos diseñar los filtros FIR. Matemáticamente, la FFT se puede escribir de la siguiente manera;
$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$Tomemos un ejemplo para entenderlo mejor. Hemos considerado ocho puntos nombrados de$x_0\quad to\quad x_7$. Elegiremos los términos pares en un grupo y los impares en el otro. A continuación se muestra una vista esquemática de lo dicho anteriormente:
Aquí, los puntos x 0 , x 2 , x 4 y x 6 se han agrupado en una categoría y, de manera similar, los puntos x 1 , x 3 , x 5 y x 7 se han colocado en otra categoría. Ahora, podemos hacerlos en un grupo de dos y podemos proceder con el cálculo. Ahora, veamos cómo esta división en dos más está ayudando en el cálculo.
$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$
$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$
$= G[k]+H[k]\times W_N^k$
Inicialmente, tomamos una secuencia de ocho puntos, pero luego la dividimos en dos partes G [k] y H [k]. G [k] representa la parte par mientras que H [k] representa la parte impar. Si queremos realizarlo a través de un diagrama, entonces se puede mostrar a continuación:
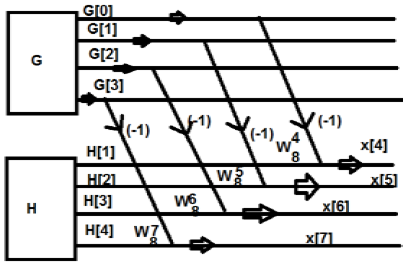
En la figura anterior, podemos ver que
$W_8^4 = -1$
$W_8^5 = -W_8^1$
$W_8^6 = -W_8^2$
$W_8^7 = -W_8^3$
Del mismo modo, los valores finales se pueden escribir de la siguiente manera:
$G[0]-H[0] = x[4]$
$G[1]-W_8^1H[1] = x[5]$
$G[2]-W_8^2H[2] = x[6]$
$G[1]-W_8^3H[3] = x[7]$
La anterior es una serie periódica. La desventaja de este sistema es que K no se puede romper más allá de los 4 puntos. Ahora, analicemos lo anterior en más. Conseguiremos las estructuras algo como esto
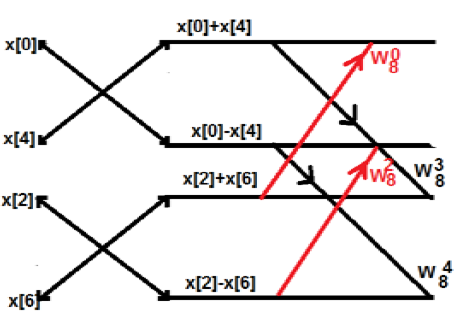
Ejemplo
Considere la secuencia x [n] = {2,1, -1, -3,0,1,2,1}. Calcule la FFT.
Solution - La secuencia dada es x [n] = {2,1, -1, -3,0,1,2,1}
Organice los términos como se muestra a continuación;
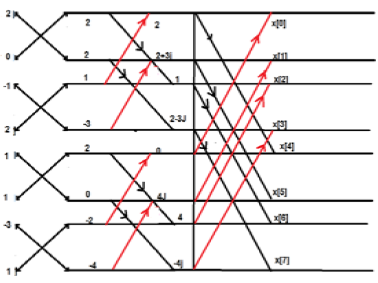
Este uso eficiente de la memoria es importante para diseñar hardware rápido para calcular la FFT. El término cálculo in situ se utiliza para describir este uso de memoria.
Diezmamiento en secuencia de tiempo
En esta estructura, representamos todos los puntos en formato binario, es decir, en 0 y 1. Luego, invertimos esas estructuras. La secuencia que obtenemos después de eso se conoce como secuencia de inversión de bits. Esto también se conoce como diezmado en secuencia de tiempo. El cálculo in situ de una DFT de ocho puntos se muestra en formato tabular, como se muestra a continuación:
| PUNTOS | FORMATO BINARIO | INVERSIÓN | PUNTOS EQUIVALENTES |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
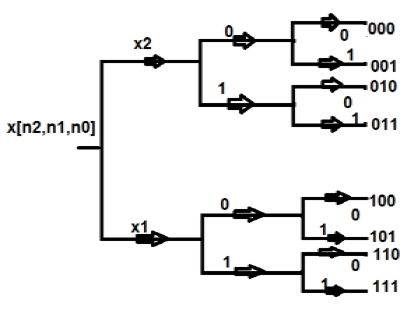
Diezmamiento en secuencia de frecuencia
Además de la secuencia de tiempo, una secuencia de N puntos también se puede representar en frecuencia. Tomemos una secuencia de cuatro puntos para entenderlo mejor.
Deja que la secuencia sea $x[0], x[1], x[2], x[3], x[4], x[5], x[6], x[7]$. Agruparemos dos puntos en un grupo, inicialmente. Matemáticamente, esta secuencia se puede escribir como;
$$x[k] = \sum_{n = 0}^{N-1}x[n]W_N^{n-k}$$Ahora hagamos un grupo de secuencia número 0 a 3 y otro grupo de secuencia 4 a 7. Ahora, matemáticamente esto se puede mostrar como;
$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[n]W_N^{nk}+\displaystyle\sum\limits_{n = N/2}^{N-1}x[n]W_N^{nk}$$Reemplacemos n por r, donde r = 0, 1, 2…. (N / 2-1). Matemáticamente,
$$\displaystyle\sum\limits_{n = 0}^{\frac{N}{2}-1}x[r]W_{N/2}^{nr}$$Tomamos los primeros cuatro puntos (x [0], x [1], x [2], x [3]) inicialmente y tratamos de representarlos matemáticamente de la siguiente manera:
$\sum_{n = 0}^3x[n]W_8^{nk}+\sum_{n = 0}^3x[n+4]W_8^{(n+4)k}$
$= \lbrace \sum_{n = 0}^3x[n]+\sum_{n = 0}^3x[n+4]W_8^{(4)k}\rbrace \times W_8^{nk}$
ahora $X[0] = \sum_{n = 0}^3(X[n]+X[n+4])$
$X[1] = \sum_{n = 0}^3(X[n]+X[n+4])W_8^{nk}$
$= [X[0]-X[4]+(X[1]-X[5])W_8^1+(X[2]-X[6])W_8^2+(X[3]-X[7])W_8^3$
Podemos dividirlo aún más en dos partes más, lo que significa que en lugar de dividirlas como una secuencia de 4 puntos, podemos dividirlas en una secuencia de 2 puntos.
Los filtros FIR pueden ser útiles para hacer un diseño asistido por computadora de los filtros. Tomemos un ejemplo y veamos cómo funciona. A continuación se muestra una figura del filtro deseado.

Mientras diseñamos por computadora, dividimos todas las figuras del gráfico continuo en valores discretos. Dentro de ciertos límites, lo dividimos en 64, 256 o 512 (y así sucesivamente) número de partes que tienen magnitudes discretas.
En el ejemplo anterior, hemos tomado límites entre -π y + π. Lo hemos dividido en 256 partes. Los puntos se pueden representar como H (0), H (1),… .hasta H (256). Aquí, aplicamos el algoritmo IDFT y esto nos dará características de fase lineal.
A veces, es posible que nos interese algún orden de filtro en particular. Digamos que queremos realizar el diseño dado anteriormente a través de un filtro de noveno orden. Entonces, tomamos valores de filtro como h0, h1, h2… .h9. Matemáticamente, se puede mostrar a continuación
$$H(e^{j\omega}) = h_0+h_1e^{-j\omega}+h_2e^{-2j\omega}+.....+h_9e^{-9j\omega}$$Donde hay una gran cantidad de dislocaciones, tomamos el máximo de puntos.
Por ejemplo, en la figura anterior, hay una caída repentina de la pendiente entre los puntos B y C. Entonces, intentamos tomar valores más discretos en este punto, pero hay una pendiente constante entre los puntos C y D. Allí tomamos menor número de valores discretos.
Para diseñar el filtro anterior, pasamos por el proceso de minimización de la siguiente manera;
$H(e^{j\omega1}) = h_0+h_1e^{-j\omega1}+h_2e^{-2j\omega1}+.....+h_9e^{-9j\omega1}$
$H(e^{j\omega2}) = h_0+h_1e^{-j\omega2}+h_2e^{-2j\omega2}+.....+h_9e^{-9j\omega2}$
Similar,
$(e^{j\omega1000}) = h_0+h_1eH^{-j\omega1000}h_2e^{-2j\omega1000}+.....+h_9+e^{-9j\omega1000}$
Al representar la ecuación anterior en forma de matriz, tenemos:
$$\begin{bmatrix}H(e^{j\omega_1})\\.\\.\\H(e^{j\omega_{1000}}) \end{bmatrix} = \begin{bmatrix}e^{-j\omega_1} & ... & e^{-j9\omega_1} \\. & & . \\. & & . \\e^{-j\omega_{1000}} &... & e^{j9\omega_{1000}} \end{bmatrix}\begin{bmatrix}h_0\\.\\.\\h_9\end{bmatrix}$$Tomemos la matriz 1000 × 1 como B, la matriz 1000 × 9 como A y la matriz 9 × 1 como $\hat{h}$.
Entonces, para resolver la matriz anterior, escribiremos
$\hat{h} = [A^TA]^{-1}A^{T}B$
$= [A^{*T}A]^{-1}A^{*T}B$
donde A * representa el conjugado complejo de la matriz A.