Connexions de circuit dans les inducteurs
Un inducteur lorsqu'il est connecté à un circuit, cette connexion peut être en série ou en parallèle. Dites-nous maintenant ce qu'il adviendra des valeurs totales de courant, de tension et de résistance s'ils sont également connectés en série, lorsqu'ils sont connectés en parallèle.
Inducteurs en série
Observons ce qui se passe, lorsque peu d'inducteurs sont connectés en série. Considérons trois résistances avec des valeurs différentes, comme le montre la figure ci-dessous.
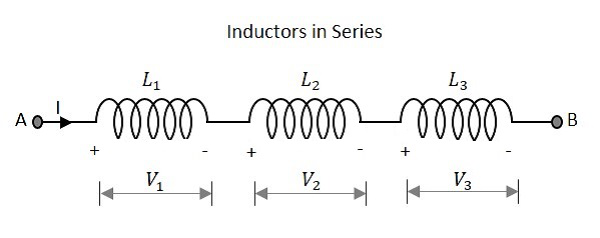
Inductance
L'inductance totale d'un circuit ayant des inductances en série est égale à la somme des inductances individuelles. La valeur d'inductance totale du réseau donnée ci-dessus est
$$ L_ {T} \: \: = \: \: L_ {1} \: \: + \: \: L_ {2} \: \: + \: \: L_ {3} $$
Où L 1 est l'inductance de la 1 ère résistance, L 2 est l'inductance de la 2 ème résistance et L 3 est l'inductance de la 3 ème résistance dans le réseau ci-dessus.
Tension
La tension totale qui apparaît à travers un réseau d'inductances en série est l'addition de chutes de tension à chaque inductance individuelle.
Tension totale qui apparaît à travers le circuit
$$ V \: \: = \: \: V_ {1} \: \: + \: \: V_ {2} \: \: + \: \: V_ {3} $$
Où V 1 est la chute de tension aux bornes 1 er inducteur, V 2 est la chute de tension aux bornes 2 nd inductance et V 3 est la chute de tension aux bornes 3 ème inducteur dans le réseau ci - dessus.
Actuel
La quantité totale de courant qui traverse un ensemble d'inducteurs connectés en série est la même en tous les points du réseau.
Le courant à travers le réseau
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Là où je 1 est le courant à travers le 1 er inducteur, je 2 est le courant à travers le 2 e inducteur et je 3 est le courant à travers le 3 ème inductance dans le réseau ci - dessus.
Inducteurs en parallèle
Observons ce qui se passe, lorsque peu de résistances sont connectées en parallèle. Considérons trois résistances avec des valeurs différentes, comme le montre la figure ci-dessous.

Inductance
L'inductance totale d'un circuit ayant des résistances parallèles est calculée différemment de la méthode de réseau d'inductance en série. Ici, la valeur réciproque (1 / R) des inductances individuelles est ajoutée à l'inverse de la somme algébrique pour obtenir la valeur d'inductance totale.
La valeur d'inductance totale du réseau est
$$ \ frac {1} {L_ {T}} \: \: = \: \: \ frac {1} {L_ {1}} \: \: + \: \: \ frac {1} {L_ { 2}} \: \: + \: \: \ frac {1} {L_ {3}} $$
Où L 1 est l'inductance de 1 er inductance, L 2 est l'inductance du 2 ème inducteur et L 3 est l'inductance du 3 ème inducteur dans le réseau ci - dessus.
De la méthode que nous avons pour calculer l'inductance parallèle, nous pouvons dériver une équation simple pour un réseau parallèle à deux inductances. Il est
$$ L_ {T} \: \: = \: \: \ frac {L_ {1} \: \: \ times \: \: L_ {2}} {L_ {1} \: \: + \: \ : L_ {2}} $$
Tension
La tension totale qui apparaît sur un réseau d'inductances parallèles est la même que les chutes de tension à chaque inductance individuelle.
La tension qui apparaît à travers le circuit
$$ V \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
Où V 1 est la chute de tension aux bornes 1 er inducteur, V 2 est la chute de tension aux bornes 2 nd inductance et V 3 est la chute de tension aux bornes 3 ème inducteur dans le réseau ci - dessus. Par conséquent, la tension est la même en tous les points d'un réseau d'inductances parallèles.
Actuel
La quantité totale de courant entrant dans un réseau inductif parallèle est la somme de tous les courants individuels circulant dans toutes les branches parallèles. La valeur d'inductance de chaque branche détermine la valeur du courant qui la traverse.
Le courant total à travers le réseau est
$$ I \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Là où je 1 est le courant à travers le 1 er inducteur, je 2 est le courant à travers le 2 e inducteur et je 3 est le courant à travers le 3 ème inductance dans le réseau ci - dessus.
Par conséquent, la somme des courants individuels dans différentes branches donne le courant total dans un réseau parallèle.
Réactance inductive
La réactance inductive est l'opposition offerte par une inductance au flux de courant alternatif, ou simplement au courant alternatif. Un inducteur a la propriété de résister au changement du flux de courant et, par conséquent, il montre une certaine opposition qui peut être appeléereactance, car la fréquence du courant d'entrée doit également être considérée avec la résistance qu'il offre.
Indication - XL
Unités - Ohms
Symbole - Ω
Dans un circuit purement inductif, le courant IL lagsla tension appliquée de 90 °. La réactance inductive est calculée par,
$$ X_ {L} \: \: = \: \: 2 \ pi fL $$
Où f est la fréquence du signal. Par conséquent, la réactance inductive est fonction de la fréquence et de l'inductance.