Électronique de base - Inductance
La propriété d'un inducteur d'obtenir la tension induite par le changement de flux de courant est définie comme l'inductance. L'inductance est le rapport de la tension au taux de variation du courant.
Le taux de changement de courant produit un changement dans le champ magnétique, ce qui induit une force électromagnétique dans la direction opposée à la source de tension. Cette propriété d'induction de l'EMF est appeléeInductance.
La formule de l'inductance est
$$ Inductance \: \: = \: \: \ frac {volatge} {rate \: of \: change \: of \: current} $$
Units −
L'unité d'inductance est Henry. Il est indiqué parL.
Les inducteurs sont pour la plupart disponibles en mH (milli Henry) et μH (micro Henry).
On dit qu'une bobine a une inductance de one Henry lorsqu'un EMF de one volt est auto-induit dans la bobine où le courant circulant a changé à une vitesse de one ampere per second.
Auto-inductance
Si l'on considère une bobine dans laquelle un certain courant circule, elle a un champ magnétique, perpendiculaire au flux de courant. Lorsque ce courant continue de varier, le champ magnétique change également et ce champ magnétique changeant, induit un EMF, opposé à la tension de source. Ce CEM opposé produit est leself-induced voltage et cette méthode est appelée comme self-inductance.
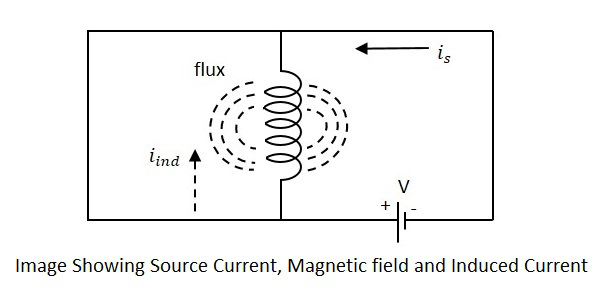
Le courant is sur la figure, indiquer le courant source pendant iindindique le courant induit. Le flux représente le flux magnétique créé autour de la bobine. Avec l'application de tension, le courantisdes flux et des flux se créent. Quand le courantis varie, le flux varie en produisant iind.
Cette CEM induite à travers la bobine est proportionnelle à la vitesse de variation du courant. Plus le taux de variation du courant est élevé, plus la valeur de l'EMF induite est élevée.
Nous pouvons écrire l'équation ci-dessus comme
$$ E \: \: \ alpha \: \: \ frac {dI} {dt} $$
$$ E \: \: = \: \: L \: \: \ frac {dI} {dt} $$
Où,
E l'EMF est-il produit
dI/dt indique le taux de variation du courant
L indique le coefficient d'inductance.
L'auto-inductance ou le coefficient d'auto-inductance peut être appelé
$$ L \: \: = \: \: \ frac {E} {\ frac {dI} {dt}} $$
L'équation réelle s'écrit
$$ E \: \: = \: \: - L \: \: \ frac {dI} {dt} $$
Le moins dans l'équation ci-dessus indique que the EMF is induced in opposite direction to the voltage source selon la loi de Lenz.
Inductance mutuelle
Comme la bobine de transport de courant produit un champ magnétique autour d'elle, si une autre bobine est amenée près de cette bobine, de sorte qu'elle se trouve dans la région de flux magnétique du primaire, alors le flux magnétique variable induit un CEM dans la seconde bobine. Si cette première bobine est appeléePrimary coil, le second peut être appelé Secondary coil.
Lorsque l'EMF est induit dans la bobine secondaire en raison du champ magnétique variable de la bobine primaire, un tel phénomène est appelé Mutual Inductance.
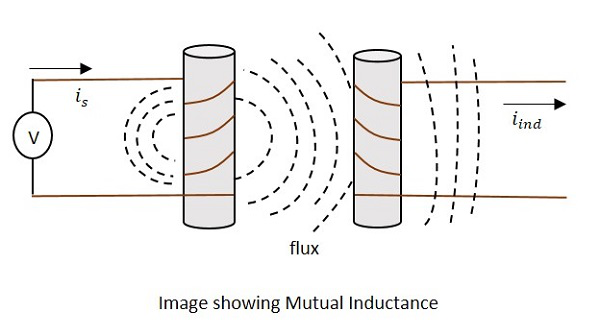
Le courant is sur la figure, indiquer le courant source pendant iindindique le courant induit. Le flux représente le flux magnétique créé autour de la bobine. Cela se propage également à la bobine secondaire.
Avec l'application de tension, le courant isdes flux et des flux se créent. Quand le courantis varie, le flux varie en produisant iind dans la bobine secondaire, en raison de la propriété d'inductance mutuelle.
Le changement a eu lieu comme ça.
$$ V_ {p} \: \: I_ {p} \ rightarrow \: \: B \: \: \ rightarrow \: \: V_ {s} \: \: I_ {s} $$
Où,
Vp ip Indiquez respectivement la tension et le courant dans la bobine primaire
B Indique le flux magnétique
Vs is Indiquez respectivement la tension et le courant dans la bobine secondaire
Inductance mutuelle M des deux circuits décrit la quantité de tension dans le secondaire induite par les changements du courant du primaire.
$$ V (Secondaire) \: \: = \: \: - M \ frac {\ Delta I} {\ Delta t} $$
Où $ \ frac {\ Delta I} {\ Delta t} $ le taux de variation du courant avec le temps et Mest le coefficient d'inductance mutuelle. Le signe moins indique la direction du courant opposée à la source.
Units −
Les unités d'inductance mutuelle sont
$$ volt \: \: = \: \: M \ frac {ampères} {sec} $$
(D'après l'équation ci-dessus)
$$ M \: \: = \: \: \ frac {volt. \: Sec} {amp} $$
$$ = \: \: Henry (H) $$
En fonction du nombre de tours des bobines primaire et secondaire, la liaison du flux magnétique et la quantité de CEM induit varient. Le nombre de tours en primaire est noté N1 et secondaire par N2. Le coefficient de couplage est le terme qui spécifie l'inductance mutuelle des deux bobines.
Facteurs affectant l'inductance
Il y a quelques facteurs qui affectent les performances d'un inducteur. Les principaux sont discutés ci-dessous.
Longueur de la bobine
La longueur de la bobine d'inductance est inversement proportionnelle à l'inductance de la bobine. Si la longueur de la bobine est supérieure, l'inductance offerte par cet inducteur diminue et vice versa.
Section transversale de la bobine
La section transversale de la bobine est directement proportionnelle à l'inductance de la bobine. Plus la surface de la bobine est élevée, plus l'inductance sera élevée.
Nombre de tours
Avec le nombre de tours, la bobine affecte directement l'inductance. La valeur de l'inductance correspond au nombre de tours de la bobine. Par conséquent, plus le nombre de tours est élevé, plus le carré de celui-ci sera la valeur de l'inductance de la bobine.
Perméabilité du noyau
le permeability (μ)du matériau du noyau de l'inducteur indique le support que le noyau fournit pour la formation d'un champ magnétique en lui-même. lehigher la perméabilité du matériau de base, le higher sera l'inductance.
Coefficient de couplage
C'est un facteur important à connaître pour le calcul de l'inductance mutuelle de deux bobines. Considérons deux bobines voisines de N1 et N2 tours respectivement.
Le courant traversant la première bobine i 1 produit un flux Ψ 1 . La quantité de liaisons de flux magnétique est comprise par weber-spires.
Soit la quantité de liaison de flux magnétique à la deuxième bobine, en raison de l'unité de courant de i 1 BE
$$ \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Cela peut être compris comme le coefficient d'inductance mutuelle, ce qui signifie
$$ M \: \: = \: \: \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
Par conséquent, le coefficient d'inductance mutuelle entre deux bobines ou circuits est compris comme les spires dans une bobine en raison de 1A de courant dans l'autre bobine.
Si l'auto-inductance de la première bobine est L 1 , alors
$$ L_ {1} i_ {1} \: \: = \: \: {N_ {1} \ varphi_ {1}} \: \: => \: \: \ frac {L_ {1}} {N_ {1}} \: \: \ frac {\ varphi_ {1}} {i_ {1}} $$
$$ M \: \: = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} $$
De même, le coefficient d'inductance mutuelle dû au courant i 2 dans la deuxième bobine est
$$ M \: \: = \: \: \ frac {N_ {1} \ varphi_ {2}} {i_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \ : 1 $$
Si l'auto-inductance de la deuxième bobine est L 2
$$ L_ {2} i_ {2} \: \: = \: \: N_ {2} \ varphi_ {2} $$
$$ \ frac {L_ {2}} {N_ {2}} \: \: = \: \: \ frac {\ varphi_ {2}} {i_ {2}} $$
Par conséquent,
$$ M \: \: = \: \: \ frac {N_ {1} L_ {2}} {N_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \: 2 $$
En multipliant 1 et 2, nous obtenons
$$ M \: \: \ times \: \: M = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} \: \: \ times \: \: \ frac { N_ {1} L_ {2}} {N_ {2}} $$
$$ M ^ {2} \: \: = \: \: L_ {1} L_ {2} \: \: => \: \: M \: \: = \: \: \ sqrt {L_ {1 } L_ {2}} $$
L'équation ci-dessus est vraie lorsque tout le flux changeant de la bobine primaire est lié à la bobine secondaire, ce qui est un cas idéal. Mais en pratique, ce n'est pas le cas. Par conséquent, nous pouvons écrire comme
$$ M \: \: \ neq \: \: \ sqrt {L_ {1} L_ {2}} $$
$$ et \ frac {M} {\ sqrt {L_ {1} L_ {2}}} \: \: = \: \: K \: \: \ neq \: \: 1 $$
Où K est connu comme le coefficient de couplage.
le Coefficient of coupling K peut être défini comme le rapport du coefficient réel d'inductance mutuelle au coefficient idéal (maximum) d'inductance mutuelle.
Si la valeur de k est proche de l'unité, alors les bobines sont dites étroitement couplées et si la valeur de k = 0, alors les bobines sont dites faiblement couplées.
Applications des inducteurs
Il existe de nombreuses applications des inducteurs, telles que -
Les inductances sont utilisées dans les circuits de filtrage pour détecter les composants haute fréquence et supprimer les signaux de bruit
Pour isoler le circuit des signaux HF indésirables.
Les inducteurs sont utilisés dans les circuits électriques pour former un transformateur et isoler les circuits des pointes.
Les inducteurs sont également utilisés dans les moteurs.