Conception de compilateurs - Automates finis
Les automates finis sont une machine à états qui prend une chaîne de symboles en entrée et change son état en conséquence. Les automates finis sont un outil de reconnaissance des expressions régulières. Lorsqu'une chaîne d'expression régulière est introduite dans des automates finis, elle change son état pour chaque littéral. Si la chaîne d'entrée est traitée avec succès et que l'automate atteint son état final, elle est acceptée, c'est-à-dire que la chaîne qui vient d'être alimentée est considérée comme un jeton valide de la langue en cours.
Le modèle mathématique des automates finis se compose de:
- Ensemble fini d'états (Q)
- Ensemble fini de symboles d'entrée (Σ)
- Un état de démarrage (q0)
- Ensemble d'états finaux (qf)
- Fonction de transition (δ)
La fonction de transition (δ) mappe l'ensemble fini d'états (Q) à un ensemble fini de symboles d'entrée (Σ), Q × Σ ➔ Q
Construction finie d'automates
Soit L (r) un langage régulier reconnu par certains automates finis (FA).
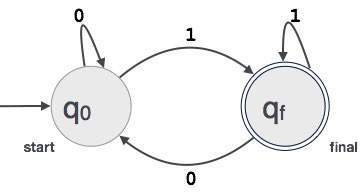
States: Les états de FA sont représentés par des cercles. Les noms d'état sont écrits à l'intérieur de cercles.
Start state: L'état à partir duquel les automates commencent, est connu comme l'état de départ. L'état de démarrage a une flèche pointée vers lui.
Intermediate states: Tous les états intermédiaires ont au moins deux flèches; un pointant vers et un autre soulignant d'eux.
Final state: Si la chaîne d'entrée est analysée avec succès, les automates devraient être dans cet état. L'état final est représenté par des doubles cercles. Il peut avoir un nombre impair de flèches pointant vers lui et un nombre pair de flèches pointant vers lui. Le nombre de flèches impaires est supérieur à pair, c'est-à-direodd = even+1.
Transition: La transition d'un état à un autre état se produit lorsqu'un symbole souhaité dans l'entrée est trouvé. Lors de la transition, les automates peuvent passer à l'état suivant ou rester dans le même état. Le mouvement d'un état à un autre est représenté par une flèche dirigée, où les flèches indiquent l'état de destination. Si les automates restent dans le même état, une flèche pointant d'un état vers lui-même est dessinée.
Example: Nous supposons que FA accepte toute valeur binaire à trois chiffres se terminant par le chiffre 1. FA = {Q (q 0 , q f ), Σ (0,1), q 0 , q f , δ}