Conception du compilateur - Analyse de la syntaxe

L'analyse ou l'analyse syntaxique est la deuxième phase d'un compilateur. Dans ce chapitre, nous allons apprendre les concepts de base utilisés dans la construction d'un analyseur syntaxique.

Nous avons vu qu'un analyseur lexical peut identifier des jetons à l'aide d'expressions régulières et de règles de modèle. Mais un analyseur lexical ne peut pas vérifier la syntaxe d'une phrase donnée en raison des limitations des expressions régulières. Les expressions régulières ne peuvent pas vérifier les jetons d'équilibrage, tels que les parenthèses. Par conséquent, cette phase utilise la grammaire sans contexte (CFG), qui est reconnue par les automates push-down.

CFG, en revanche, est un sur-ensemble de la grammaire régulière, comme illustré ci-dessous:

Cela implique que chaque grammaire régulière est également sans contexte, mais il existe des problèmes qui dépassent le cadre de la grammaire régulière. CFG est un outil utile pour décrire la syntaxe des langages de programmation.

Grammaire sans contexte

Dans cette section, nous allons d'abord voir la définition de la grammaire sans contexte et introduire les terminologies utilisées dans la technologie d'analyse.

Une grammaire sans contexte comporte quatre composants:

Un ensemble de non-terminals(V). Les non-terminaux sont des variables syntaxiques qui désignent des ensembles de chaînes. Les non-terminaux définissent des ensembles de chaînes qui aident à définir le langage généré par la grammaire.
Un ensemble de jetons, appelé terminal symbols(Σ). Les terminaux sont les symboles de base à partir desquels les chaînes sont formées.
Un ensemble de productions(P). Les productions d'une grammaire précisent la manière dont les terminaux et les non-terminaux peuvent être combinés pour former des chaînes. Chaque production se compose d'unnon-terminal appelé le côté gauche de la production, une flèche et une séquence de jetons et / ou on- terminals, a appelé le côté droit de la production.
L'un des non-terminaux est désigné comme le symbole de départ (S); d'où commence la production.

Les chaînes sont dérivées du symbole de départ en remplaçant à plusieurs reprises un non-terminal (initialement le symbole de départ) par le côté droit d'une production, pour ce non-terminal.

Exemple

Nous prenons le problème du langage palindrome, qui ne peut être décrit au moyen de l'expression régulière. Autrement dit, L = {w | w = w ^R } n'est pas un langage régulier. Mais il peut être décrit au moyen de CFG, comme illustré ci-dessous:

G = ( V, Σ, P, S )

Où:

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

Cette grammaire décrit le langage palindrome, tel que: 1001, 11100111, 00100, 1010101, 11111, etc.

Analyseurs de syntaxe

Un analyseur de syntaxe ou un parseur prend l'entrée d'un analyseur lexical sous la forme de flux de jetons. L'analyseur analyse le code source (jeton stream) par rapport aux règles de production pour détecter toute erreur dans le code. La sortie de cette phase est unparse tree.

De cette façon, l'analyseur accomplit deux tâches, à savoir, analyser le code, rechercher les erreurs et générer un arbre d'analyse en sortie de la phase.

On s'attend à ce que les analyseurs analysent tout le code même si des erreurs existent dans le programme. Les analyseurs utilisent des stratégies de récupération d'erreurs, que nous apprendrons plus loin dans ce chapitre.

Dérivation

Une dérivation est essentiellement une séquence de règles de production, afin d'obtenir la chaîne d'entrée. Au cours de l'analyse, nous prenons deux décisions pour une forme d'entrée sensible:

Décider du non-terminal qui doit être remplacé.
Décider de la règle de production par laquelle le non-terminal sera remplacé.

Pour décider du non-terminal à remplacer par la règle de production, nous pouvons avoir deux options.

Dérivation la plus à gauche

Si la forme sententielle d'une entrée est scannée et remplacée de gauche à droite, elle est appelée dérivation la plus à gauche. La forme sententielle dérivée de la dérivation la plus à gauche est appelée la forme sententielle gauche.

Dérivation la plus à droite

Si nous analysons et remplaçons l'entrée par des règles de production, de droite à gauche, on parle de dérivation la plus à droite. La forme sententielle dérivée de la dérivation la plus à droite est appelée la forme sententielle droite.

Example

Règles de production:

E → E + E
E → E * E
E → id

Chaîne d'entrée: id + id * id

La dérivation la plus à gauche est:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

Notez que le côté non terminal le plus à gauche est toujours traité en premier.

La dérivation la plus à droite est:

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

Analyser l'arbre

Un arbre d'analyse est une représentation graphique d'une dérivation. Il est pratique de voir comment les chaînes sont dérivées du symbole de début. Le symbole de début de la dérivation devient la racine de l'arborescence d'analyse. Voyons cela par un exemple du dernier sujet.

Nous prenons la dérivation la plus à gauche de a + b * c

La dérivation la plus à gauche est:

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
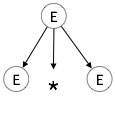
E → id + id * id

Étape 1:

E → E * E

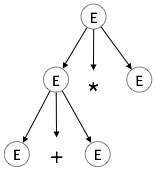
Étape 2:

E → E + E * E

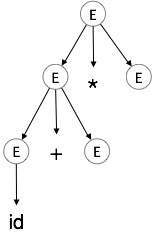
Étape 3:

E → id + E * E

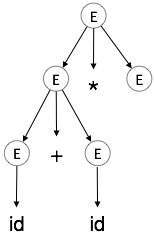
Étape 4:

E → id + id * E

Étape 5:

E → id + id * id

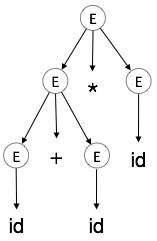
Dans un arbre d'analyse:

Tous les nœuds feuilles sont des terminaux.
Tous les nœuds intérieurs sont des non-terminaux.
Le parcours dans l'ordre donne la chaîne d'entrée d'origine.

Un arbre d'analyse représente l'associativité et la priorité des opérateurs. Le sous-arbre le plus profond est parcouru en premier, donc l'opérateur de ce sous-arbre a la priorité sur l'opérateur qui se trouve dans les nœuds parents.

Ambiguïté

Une grammaire G est dite ambiguë si elle a plus d'un arbre d'analyse (dérivation gauche ou droite) pour au moins une chaîne.

Example

E → E + E
E → E – E
E → id

Pour la chaîne id + id - id, la grammaire ci-dessus génère deux arbres d'analyse:

Le langage généré par une grammaire ambiguë est dit inherently ambiguous. L'ambiguïté dans la grammaire n'est pas bonne pour la construction d'un compilateur. Aucune méthode ne peut détecter et supprimer l'ambiguïté automatiquement, mais elle peut être supprimée soit en réécrivant la grammaire entière sans ambiguïté, soit en définissant et en suivant les contraintes d'associativité et de précédence.

Associativité

Si un opérande a des opérateurs des deux côtés, le côté sur lequel l'opérateur prend cet opérande est décidé par l'associativité de ces opérateurs. Si l'opération est associative à gauche, l'opérande sera pris par l'opérateur de gauche ou si l'opération est associative à droite, l'opérateur de droite prendra l'opérande.

Example

Les opérations telles que l'addition, la multiplication, la soustraction et la division sont laissées associatives. Si l'expression contient:

id op id op id

il sera évalué comme:

(id op id) op id

Par exemple, (id + id) + id

Les opérations comme l'exponentiation sont associatives correctes, c'est-à-dire que l'ordre d'évaluation dans la même expression sera:

id op (id op id)

Par exemple, id ^ (id ^ id)

Priorité

Si deux opérateurs différents partagent un opérande commun, la priorité des opérateurs décide de celui qui prendra l'opérande. Autrement dit, 2 + 3 * 4 peut avoir deux arbres d'analyse différents, l'un correspondant à (2 + 3) * 4 et l'autre correspondant à 2+ (3 * 4). En définissant la priorité parmi les opérateurs, ce problème peut être facilement supprimé. Comme dans l'exemple précédent, mathématiquement * (multiplication) a priorité sur + (addition), donc l'expression 2 + 3 * 4 sera toujours interprétée comme:

2 + (3 * 4)

Ces méthodes réduisent les risques d'ambiguïté dans une langue ou sa grammaire.

Récursivité gauche

Une grammaire devient récursive à gauche si elle a un 'A' non terminal dont la dérivation contient 'A' lui-même comme symbole le plus à gauche. La grammaire récursive à gauche est considérée comme une situation problématique pour les analyseurs de haut en bas. Les analyseurs de haut en bas commencent l'analyse à partir du symbole Start, qui en lui-même n'est pas terminal. Ainsi, lorsque l'analyseur rencontre le même non-terminal dans sa dérivation, il devient difficile pour lui de juger quand arrêter l'analyse du non-terminal gauche et il entre dans une boucle infinie.

Example:

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1) est un exemple de récursion immédiate à gauche, où A est n'importe quel symbole non-terminal et α représente une chaîne de non-terminaux.

(2) est un exemple de récursion indirecte à gauche.

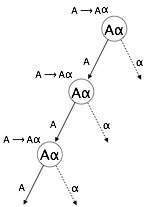
Un analyseur de haut en bas analysera d'abord le A, qui à son tour produira une chaîne composée de A lui-même et l'analyseur peut entrer dans une boucle pour toujours.

Suppression de la récursivité gauche

Une façon de supprimer la récursivité à gauche consiste à utiliser la technique suivante:

La production

A => Aα | β

est converti en productions suivantes

A => βA'
A'=> αA' | ε

Cela n'affecte pas les chaînes dérivées de la grammaire, mais supprime la récursivité gauche immédiate.

La deuxième méthode consiste à utiliser l'algorithme suivant, qui devrait éliminer toutes les récursions directes et indirectes à gauche.

START

Arrange non-terminals in some order like A1, A2, A3,…, A_n

   for each i from 1 to n
      {
      for each j from 1 to i-1
         {
         replace each production of form A_i ⟹Aj
         with A_i ⟹ δ1  | δ2 | δ3 |…|  
         where A_j ⟹ δ₁ | δ₂|…| δ_n  are current A_j productions
         }
      }
   eliminate immediate left-recursion
   
END

Example

L'ensemble de production

S => Aα | β 
A => Sd

après avoir appliqué l'algorithme ci-dessus, devrait devenir

S => Aα | β 
A => Aαd | βd

puis supprimez la récursivité gauche immédiate en utilisant la première technique.

A  => βdA'
A' => αdA' | ε

Désormais, aucune partie de la production n'a de récursivité gauche directe ou indirecte.

Affacturage gauche

Si plusieurs règles de production de grammaire ont une chaîne de préfixe commune, alors l'analyseur de haut en bas ne peut pas faire un choix quant à la production à prendre pour analyser la chaîne en cours.

Example

Si un analyseur de haut en bas rencontre une production comme

A ⟹ αβ | α | …

Ensuite, il ne peut pas déterminer quelle production suivre pour analyser la chaîne car les deux productions partent du même terminal (ou non-terminal). Pour supprimer cette confusion, nous utilisons une technique appelée affacturage gauche.

La factorisation à gauche transforme la grammaire pour la rendre utile pour les analyseurs de haut en bas. Dans cette technique, nous faisons une production pour chaque préfixe commun et le reste de la dérivation est ajouté par de nouvelles productions.

Example

Les productions ci-dessus peuvent être écrites comme

A => αA'
A'=> β |  | …

Désormais, l'analyseur n'a qu'une production par préfixe, ce qui facilite la prise de décision.

Ensembles premier et suivi

Une partie importante de la construction de la table d'analyseur consiste à créer les premiers ensembles et les suivants. Ces ensembles peuvent fournir la position réelle de n'importe quel terminal dans la dérivation. Ceci est fait pour créer la table d'analyse où la décision de remplacer T [A, t] = α par une règle de production.

Premier set

Cet ensemble est créé pour savoir quel symbole de terminal est dérivé en première position par un non-terminal. Par exemple,

α → t β

C'est-à-dire que α dérive t (terminal) dans la toute première position. Donc, t ∈ PREMIER (α).

Algorithme de calcul du premier jeu

Regardez la définition de FIRST (α) set:

si α est un terminal, alors FIRST (α) = {α}.
si α est un non-terminal et α → ℇ est une production, alors FIRST (α) = {ℇ}.
si α est un non-terminal et α → 1 2 3… n et tout FIRST () contient t alors t est dans FIRST (α).

Le premier ensemble peut être vu comme:

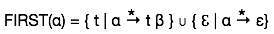
Suivez l'ensemble

De même, nous calculons quel symbole terminal suit immédiatement un α non terminal dans les règles de production. Nous ne considérons pas ce que le non-terminal peut générer mais au contraire, nous voyons quel serait le prochain symbole terminal qui suivrait les productions d'un non-terminal.

Algorithme de calcul de l'ensemble de suivi:

si α est un symbole de départ, alors FOLLOW () = $
si α est un non-terminal et a une production α → AB, alors FIRST (B) est dans FOLLOW (A) sauf ℇ.
si α est un non-terminal et a une production α → AB, où B ℇ, alors FOLLOW (A) est dans FOLLOW (α).

L'ensemble de suivi peut être vu comme suit: FOLLOW (α) = {t | S * αt *}

Limitations des analyseurs de syntaxe

Les analyseurs de syntaxe reçoivent leurs entrées, sous forme de jetons, des analyseurs lexicaux. Les analyseurs lexicaux sont responsables de la validité d'un token fourni par l'analyseur de syntaxe. Les analyseurs de syntaxe présentent les inconvénients suivants -

il ne peut pas déterminer si un jeton est valide,
il ne peut pas déterminer si un jeton est déclaré avant d'être utilisé,
il ne peut pas déterminer si un jeton est initialisé avant d'être utilisé,
il ne peut pas déterminer si une opération effectuée sur un type de jeton est valide ou non.

Ces tâches sont accomplies par l'analyseur sémantique, que nous étudierons dans l'analyse sémantique.