Conception du compilateur - Analyseur de haut en bas
Nous avons appris dans le dernier chapitre que la technique d'analyse descendante analyse l'entrée et commence à construire un arbre d'analyse à partir du nœud racine en descendant progressivement vers les nœuds feuilles. Les types d'analyse descendante sont décrits ci-dessous:
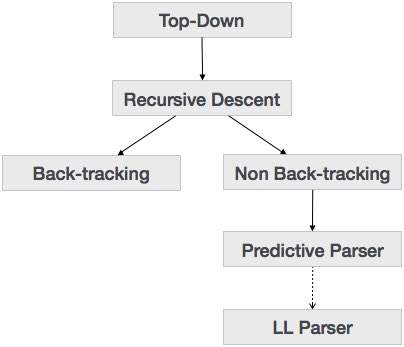
Analyse de descente récursive
La descente récursive est une technique d'analyse descendante qui construit l'arbre d'analyse à partir du haut et l'entrée est lue de gauche à droite. Il utilise des procédures pour chaque entité terminale et non terminale. Cette technique d'analyse analyse récursivement l'entrée pour créer un arbre d'analyse, qui peut ou non nécessiter un suivi arrière. Mais la grammaire qui lui est associée (si elle n'est pas prise en compte) ne peut éviter le retour en arrière. Une forme d'analyse de descente récursive qui ne nécessite aucun suivi arrière est appeléepredictive parsing.
Cette technique d'analyse est considérée comme récursive car elle utilise une grammaire sans contexte qui est de nature récursive.
Suivi de retour
Les analyseurs de haut en bas partent du nœud racine (symbole de début) et comparent la chaîne d'entrée aux règles de production pour les remplacer (si elles correspondent). Pour comprendre cela, prenez l'exemple suivant de CFG:
S → rXd | rZd
X → oa | ea
Z → aiPour une chaîne d'entrée: read, un analyseur de haut en bas, se comportera comme ceci:
Il commencera par S des règles de production et fera correspondre son rendement à la lettre la plus à gauche de l'entrée, c'est-à-dire «r». La production même de S (S → rXd) y correspond. Ainsi, l'analyseur de haut en bas avance à la lettre d'entrée suivante (c'est-à-dire «e»). L'analyseur essaie d'étendre 'X' non-terminal et vérifie sa production depuis la gauche (X → oa). Il ne correspond pas au symbole d'entrée suivant. Ainsi, l'analyseur descendant fait marche arrière pour obtenir la prochaine règle de production de X, (X → ea).
Maintenant, l'analyseur fait correspondre toutes les lettres d'entrée de manière ordonnée. La chaîne est acceptée.
|
|
|
|
|
Analyseur prédictif
L'analyseur prédictif est un analyseur de descente récursive, qui a la capacité de prédire quelle production doit être utilisée pour remplacer la chaîne d'entrée. L'analyseur prédictif ne souffre pas de retour en arrière.
Pour accomplir ses tâches, l'analyseur prédictif utilise un pointeur d'anticipation, qui pointe vers les symboles d'entrée suivants. Pour rendre l'analyseur de retour libre, l'analyseur prédictif impose des contraintes sur la grammaire et n'accepte qu'une classe de grammaire connue sous le nom de grammaire LL (k).
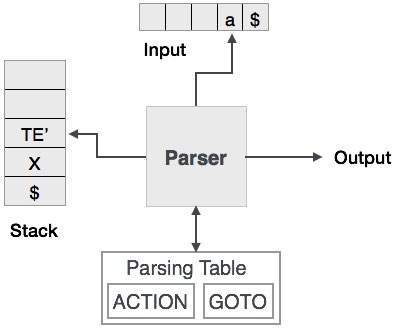
L'analyse prédictive utilise une pile et une table d'analyse pour analyser l'entrée et générer un arbre d'analyse. La pile et l'entrée contiennent un symbole de fin$pour indiquer que la pile est vide et que l'entrée est consommée. L'analyseur se réfère à la table d'analyse pour prendre toute décision sur la combinaison des éléments d'entrée et de pile.
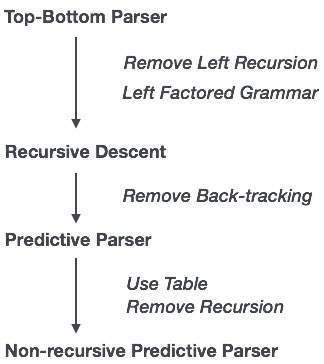
Dans l'analyse de descente récursive, l'analyseur peut avoir plus d'une production à choisir pour une seule instance d'entrée, tandis que dans l'analyseur prédictif, chaque étape a au plus une production à choisir. Il peut y avoir des cas où aucune production ne correspond à la chaîne d'entrée, ce qui entraîne l'échec de la procédure d'analyse.
Analyseur LL
Un analyseur LL accepte la grammaire LL. La grammaire LL est un sous-ensemble de la grammaire sans contexte mais avec quelques restrictions pour obtenir la version simplifiée, afin de réaliser une implémentation facile. La grammaire LL peut être implémentée au moyen des deux algorithmes à savoir, descente récursive ou pilotée par table.
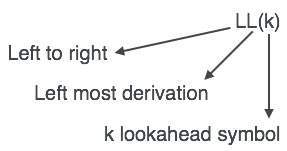
L'analyseur LL est noté LL (k). Le premier L dans LL (k) analyse l'entrée de gauche à droite, le second L dans LL (k) représente la dérivation la plus à gauche et k lui-même représente le nombre d'anticipations. Généralement k = 1, donc LL (k) peut aussi s'écrire LL (1).
Algorithme d'analyse LL
Nous pouvons nous en tenir à LL (1) déterministe pour l'explication de l'analyseur, car la taille de la table croît exponentiellement avec la valeur de k. Deuxièmement, si une grammaire donnée n'est pas LL (1), alors généralement, ce n'est pas LL (k), pour tout k donné.
Ci-dessous est un algorithme pour l'analyse LL (1):
Input:
string ω
parsing table M for grammar G
Output:
If ω is in L(G) then left-most derivation of ω,
error otherwise.
Initial State : $S on stack (with S being start symbol)
ω$ in the input buffer
SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ Vt or $
if X = a
POP X and advance ip.
else
error()
endif
else /* X is non-terminal */
if M[X,a] = X → Y1, Y2,... Yk
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
Output the production X → Y1, Y2,... Yk
else
error()
endif
endif
until X = $ /* empty stack */Une grammaire G est LL (1) si A → α | β sont deux productions distinctes de G:
pour aucun terminal, α et β dérivent des chaînes commençant par a.
au plus un des α et β peut dériver une chaîne vide.
si β → t, alors α ne dérive aucune chaîne commençant par un terminal dans FOLLOW (A).