Guide rapide
Dans le monde moderne de l'électronique, le terme Digital est généralement associé à un ordinateur car le terme Digitalest dérivé de la façon dont les ordinateurs exécutent leurs opérations, en comptant les chiffres. Pendant de nombreuses années, l'application de l'électronique numérique était uniquement dans le système informatique. Mais de nos jours, l'électronique numérique est utilisée dans de nombreuses autres applications. Voici quelques exemples dans lesquelsDigital electronics est fortement utilisé.
- Contrôle des processus industriels
- Système militaire
- Television
- Système de communication
- Équipement médical
- Radar
- Navigation
Signal
Signalpeut être définie comme une quantité physique, qui contient des informations. C'est une fonction d'une ou plusieurs variables indépendantes. Les signaux sont de deux types.
- Signal analogique
- Signal numérique
Signal analogique
Un analog signalest défini comme le signal ayant des valeurs continues. Le signal analogique peut avoir un nombre infini de valeurs différentes. Dans le scénario du monde réel, la plupart des choses observées dans la nature sont analogues. Voici des exemples de signaux analogiques.
- Temperature
- Pressure
- Distance
- Sound
- Voltage
- Current
- Power
Représentation graphique du signal analogique (température)
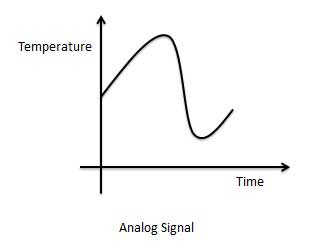
Les circuits qui traitent les signaux analogiques sont appelés circuits ou système analogiques. Des exemples du système analogique sont suivants.
- Filter
- Amplifiers
- Récepteur de télévision
- Contrôleur de vitesse du moteur
Inconvénient des systèmes analogiques
- Moins de précision
- Moins de polyvalence
- Plus d'effet de bruit
- Plus de distorsion
- Plus d'effet du temps
Signal numérique
UNE digital signalest défini comme le signal qui n'a qu'un nombre fini de valeurs distinctes. Les signaux numériques ne sont pas des signaux continus. Dans le calculateur électronique numérique, l'entrée est donnée à l'aide de commutateurs. Cette entrée est convertie en signal électrique qui a deux valeurs discrètes ou niveaux. L'un de ceux-ci peut être appelé niveau bas et un autre est appelé niveau élevé. Le signal sera toujours l'un des deux niveaux. Ce type de signal est appelé signal numérique. Voici des exemples de signal numérique.
- Signal binaire
- Signal octal
- Signal hexadécimal
Représentation graphique du signal numérique (binaire)
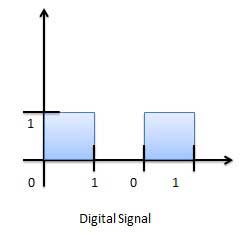
Les circuits qui traitent les signaux numériques sont appelés systèmes numériques ou circuits numériques. Voici des exemples de systèmes numériques.
- Registers
- Flip-flop
- Counters
- Microprocessors
Avantage des systèmes numériques
- Plus de précision
- Plus de polyvalence
- Moins de distorsion
- Communiquez facilement
- Stockage possible d'informations
Comparaison du signal analogique et numérique
| SN | Signal analogique | Signal numérique |
|---|---|---|
| 1 | Le signal analogique a des valeurs infinies. | Le signal numérique a un nombre fini de valeurs. |
| 2 | Le signal analogique a un caractère continu. | Le signal numérique a un caractère discret. |
| 3 | Le signal analogique est généré par des transducteurs et des générateurs de signaux. | Le signal numérique est généré par un convertisseur A vers D. |
| 4 | Exemple de signal analogique - onde sinusoïdale, onde triangulaire. | Exemple de signal numérique - signal binaire. |
Un système numérique ne peut comprendre le système de numération positionnelle que là où il y a quelques symboles appelés chiffres et ces symboles représentent des valeurs différentes en fonction de la position qu'ils occupent dans le nombre.
Une valeur de chaque chiffre dans un nombre peut être déterminée en utilisant
Le chiffre
La position du chiffre dans le nombre
La base du système numérique (où base est définie comme le nombre total de chiffres disponibles dans le système numérique).
Système de nombres décimaux
Le système numérique que nous utilisons dans notre vie de tous les jours est le système numérique décimal. Le système de nombres décimaux a la base 10 car il utilise 10 chiffres de 0 à 9. Dans le système de nombres décimaux, les positions successives à gauche du point décimal représentent des unités, des dizaines, des centaines, des milliers et ainsi de suite.
Chaque position représente une puissance spécifique de la base (10). Par exemple, le nombre décimal 1234 se compose du chiffre 4 dans la position des unités, 3 dans la position des dizaines, 2 dans la position des centaines et 1 dans la position des milliers, et sa valeur peut être écrite comme
(1×1000) + (2×100) + (3×10) + (4×l)
(1×103) + (2×102) + (3×101) + (4×l00)
1000 + 200 + 30 + 1
1234En tant que programmeur informatique ou professionnel de l'informatique, vous devez comprendre les systèmes numériques suivants qui sont fréquemment utilisés dans les ordinateurs.
| SN | Système de numérotation et description |
|---|---|
| 1 | Binary Number System Base 2. Chiffres utilisés: 0, 1 |
| 2 | Octal Number System Base 8. Chiffres utilisés: 0 à 7 |
| 3 | Hexa Decimal Number System Base 16. Chiffres utilisés: 0 à 9, Lettres utilisées: A- F |
Système de numération binaire
Caractéristiques
Utilise deux chiffres, 0 et 1.
Aussi appelé système numérique de base 2
Chaque position dans un nombre binaire représente une puissance 0 de la base (2). Exemple: 2 0
La dernière position dans un nombre binaire représente une puissance x de la base (2). Exemple: 2 x où x représente la dernière position - 1.
Exemple
Nombre binaire: 10101 2
Calcul de l'équivalent décimal -
| Étape | Nombre binaire | Nombre décimal |
|---|---|---|
| Étape 1 | 10101 2 | ((1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| Étape 2 | 10101 2 | (16 + 0 + 4 + 0 + 1) 10 |
| Étape 3 | 10101 2 | 21 10 |
Note:10101 2 s'écrit normalement 10101.
Système de nombre octal
Caractéristiques
Utilise huit chiffres, 0,1,2,3,4,5,6,7.
Aussi appelé système numérique de base 8
Chaque position dans un nombre octal représente une puissance 0 de la base (8). Exemple: 8 0
La dernière position dans un nombre octal représente une puissance x de la base (8). Exemple: 8 x où x représente la dernière position - 1.
Exemple
Numéro octal - 12570 8
Calcul de l'équivalent décimal -
| Étape | Numéro octal | Nombre décimal |
|---|---|---|
| Étape 1 | 12570 8 | ((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10 |
| Étape 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| Étape 3 | 12570 8 | 5496 10 |
Note:12570 8 s'écrit normalement 12570.
Système de nombres hexadécimaux
Caractéristiques
Utilise 10 chiffres et 6 lettres, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
Les lettres représentent des nombres commençant à 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Aussi appelé système de numérotation de base 16.
Chaque position dans un nombre hexadécimal représente une puissance 0 de la base (16). Exemple 16 0 .
La dernière position dans un nombre hexadécimal représente une puissance x de la base (16). Exemple 16 x où x représente la dernière position - 1.
Exemple -
Nombre hexadécimal: 19FDE 16
Calcul de l'équivalent décimal -
| Étape | Nombre hexadécimal | Nombre décimal |
|---|---|---|
| Étape 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Étape 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| Étape 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| Étape 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 s'écrit normalement 19FDE.
Il existe de nombreuses méthodes ou techniques qui peuvent être utilisées pour convertir des nombres d'une base à une autre. Nous allons démontrer ici ce qui suit -
- Décimal à un autre système de base
- Autre système de base en décimal
- Autre système de base non décimal
- Méthode de raccourci - Binaire vers Octal
- Méthode de raccourci - Octal vers binaire
- Méthode de raccourci - Binaire à hexadécimal
- Méthode de raccourci - Hexadécimal à binaire
Décimal à un autre système de base
Pas
Step 1 - Divisez le nombre décimal à convertir par la valeur de la nouvelle base.
Step 2 - Obtenez le reste de l'étape 1 comme le chiffre le plus à droite (chiffre le moins significatif) du nouveau numéro de base.
Step 3 - Divisez le quotient de la division précédente par la nouvelle base.
Step 4 - Enregistrez le reste de l'étape 3 comme chiffre suivant (à gauche) du nouveau numéro de base.
Répétez les étapes 3 et 4, en obtenant les restes de droite à gauche, jusqu'à ce que le quotient devienne zéro à l'étape 3.
Le dernier reste ainsi obtenu sera le chiffre le plus significatif (MSD) du nouveau numéro de base.
Exemple -
Nombre décimal: 29 10
Calcul de l'équivalent binaire -
| Étape | Opération | Résultat | Reste |
|---|---|---|---|
| Étape 1 | 29/2 | 14 | 1 |
| Étape 2 | 14/2 | sept | 0 |
| Étape 3 | 7/2 | 3 | 1 |
| Étape 4 | 3/2 | 1 | 1 |
| Étape 5 | 1/2 | 0 | 1 |
Comme mentionné aux étapes 2 et 4, les restes doivent être disposés dans l'ordre inverse de sorte que le premier reste devienne le chiffre le moins significatif (LSD) et le dernier reste le chiffre le plus significatif (MSD).
Nombre décimal - 29 10 = Nombre binaire - 11101 2 .
Autre système de base au système décimal
Pas
Step 1 - Déterminez la valeur de colonne (positionnelle) de chaque chiffre (cela dépend de la position du chiffre et de la base du système numérique).
Step 2 - Multipliez les valeurs de colonne obtenues (à l'étape 1) par les chiffres des colonnes correspondantes.
Step 3 - Additionner les produits calculés à l'étape 2. Le total est la valeur équivalente en décimal.
Exemple
Nombre binaire - 11101 2
Calcul de l'équivalent décimal -
| Étape | Nombre binaire | Nombre décimal |
|---|---|---|
| Étape 1 | 11101 2 | ((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| Étape 2 | 11101 2 | (16 + 8 + 4 + 0 + 1) 10 |
| Étape 3 | 11101 2 | 29 10 |
Nombre binaire - 11101 2 = Nombre décimal - 29 10
Autre système de base au système non décimal
Pas
Step 1 - Convertissez le nombre d'origine en nombre décimal (base 10).
Step 2 - Convertissez le nombre décimal ainsi obtenu en nouveau nombre de base.
Exemple
Numéro octal - 25 8
Calcul de l'équivalent binaire -
Étape 1 - Convertir en décimal
| Étape | Numéro octal | Nombre décimal |
|---|---|---|
| Étape 1 | 25 8 | ((2 × 8 1 ) + (5 × 8 0 )) 10 |
| Étape 2 | 25 8 | (16 + 5) 10 |
| Étape 3 | 25 8 | 21 10 |
Nombre octal - 25 8 = Nombre décimal - 21 10
Étape 2 - Conversion décimale en binaire
| Étape | Opération | Résultat | Reste |
|---|---|---|---|
| Étape 1 | 21/2 | dix | 1 |
| Étape 2 | 10/2 | 5 | 0 |
| Étape 3 | 5/2 | 2 | 1 |
| Étape 4 | 2/2 | 1 | 0 |
| Étape 5 | 1/2 | 0 | 1 |
Nombre décimal - 21 10 = Nombre binaire - 10101 2
Nombre octal - 25 8 = Nombre binaire - 10101 2
Méthode de raccourci - Binaire vers Octal
Pas
Step 1 - Divisez les chiffres binaires en groupes de trois (en commençant par la droite).
Step 2 - Convertissez chaque groupe de trois chiffres binaires en un chiffre octal.
Exemple
Nombre binaire - 10101 2
Calcul de l'équivalent octal -
| Étape | Nombre binaire | Numéro octal |
|---|---|---|
| Étape 1 | 10101 2 | 010 101 |
| Étape 2 | 10101 2 | 2 8 5 8 |
| Étape 3 | 10101 2 | 25 8 |
Nombre binaire - 10101 2 = Nombre octal - 25 8
Méthode de raccourci - Octal vers binaire
Pas
Step 1 - Convertir chaque chiffre octal en un nombre binaire à 3 chiffres (les chiffres octaux peuvent être traités comme décimaux pour cette conversion).
Step 2 - Combinez tous les groupes binaires résultants (de 3 chiffres chacun) en un seul nombre binaire.
Exemple
Numéro octal - 25 8
Calcul de l'équivalent binaire -
| Étape | Numéro octal | Nombre binaire |
|---|---|---|
| Étape 1 | 25 8 | 2 10 5 10 |
| Étape 2 | 25 8 | 010 2 101 2 |
| Étape 3 | 25 8 | 010101 2 |
Nombre octal - 25 8 = Nombre binaire - 10101 2
Méthode de raccourci - Binaire à hexadécimal
Pas
Step 1 - Divisez les chiffres binaires en groupes de quatre (en commençant par la droite).
Step 2 - Convertissez chaque groupe de quatre chiffres binaires en un symbole hexadécimal.
Exemple
Nombre binaire - 10101 2
Calcul de l'équivalent hexadécimal -
| Étape | Nombre binaire | Nombre hexadécimal |
|---|---|---|
| Étape 1 | 10101 2 | 0001 0101 |
| Étape 2 | 10101 2 | 1 10 5 10 |
| Étape 3 | 10101 2 | 15 16 |
Nombre binaire - 10101 2 = Nombre hexadécimal - 15 16
Méthode de raccourci - Hexadécimal à binaire
Pas
Step 1 - Convertissez chaque chiffre hexadécimal en un nombre binaire à 4 chiffres (les chiffres hexadécimaux peuvent être traités comme décimaux pour cette conversion).
Step 2 - Combinez tous les groupes binaires résultants (de 4 chiffres chacun) en un seul nombre binaire.
Exemple
Nombre hexadécimal - 15 16
Calcul de l'équivalent binaire -
| Étape | Nombre hexadécimal | Nombre binaire |
|---|---|---|
| Étape 1 | 15 16 | 1 10 5 10 |
| Étape 2 | 15 16 | 0001 2 0101 2 |
| Étape 3 | 15 16 | 00010101 2 |
Nombre hexadécimal - 15 16 = Nombre binaire - 10101 2
Dans le codage, lorsque des nombres, des lettres ou des mots sont représentés par un groupe spécifique de symboles, on dit que le nombre, la lettre ou le mot est codé. Le groupe de symboles est appelé sous forme de code. Les données numériques sont représentées, stockées et transmises sous forme de groupe de bits binaires. Ce groupe est également appelébinary code. Le code binaire est représenté par le nombre ainsi que par une lettre alphanumérique.
Avantages du code binaire
Voici la liste des avantages offerts par le code binaire.
Les codes binaires conviennent aux applications informatiques.
Les codes binaires conviennent aux communications numériques.
Les codes binaires font l'analyse et la conception des circuits numériques si nous utilisons les codes binaires.
Puisque seuls 0 & 1 sont utilisés, la mise en œuvre devient facile.
Classification des codes binaires
Les codes sont généralement classés dans les quatre catégories suivantes.
- Codes pondérés
- Codes non pondérés
- Code décimal codé binaire
- Codes alphanumériques
- Codes de détection d'erreur
- Codes de correction d'erreur
Codes pondérés
Les codes binaires pondérés sont les codes binaires qui obéissent au principe du poids positionnel. Chaque position du nombre représente un poids spécifique. Plusieurs systèmes de codes sont utilisés pour exprimer les chiffres décimaux de 0 à 9. Dans ces codes, chaque chiffre décimal est représenté par un groupe de quatre bits.
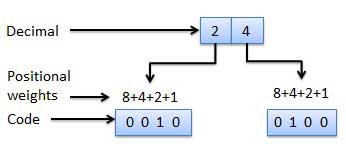
Codes non pondérés
Dans ce type de codes binaires, les poids de position ne sont pas attribués. Les exemples de codes non pondérés sont le code Excess-3 et le code Gray.
Code Excess-3
Le code Excess-3 est également appelé code XS-3. C'est un code non pondéré utilisé pour exprimer des nombres décimaux. Les mots de code Excess-3 sont dérivés des mots de code 8421 BCD ajoutant (0011) 2 ou (3) 10 à chaque mot de code en 8421. Les codes de surplus-3 sont obtenus comme suit -

Exemple
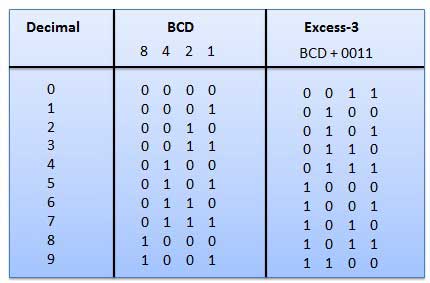
Code gris
C'est le code non pondéré et ce ne sont pas des codes arithmétiques. Cela signifie qu'aucun poids spécifique n'est attribué à la position du bit. Il a une fonction très spéciale qui, un seul bit changera chaque fois que le nombre décimal est incrémenté comme indiqué sur la fig. Comme un seul bit change à la fois, le code gris est appelé comme code de distance unitaire. Le code gris est un code cyclique. Le code Gray ne peut pas être utilisé pour les opérations arithmétiques.
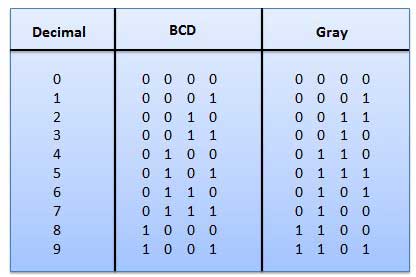
Application du code Gray
Le code gris est couramment utilisé dans les codeurs de position d'arbre.
Un codeur de position d'arbre produit un mot de code qui représente la position angulaire de l'arbre.
Code décimal codé binaire (BCD)
Dans ce code, chaque chiffre décimal est représenté par un nombre binaire de 4 bits. BCD est un moyen d'exprimer chacun des chiffres décimaux avec un code binaire. Dans le BCD, avec quatre bits, nous pouvons représenter seize nombres (0000 à 1111). Mais dans le code BCD, seuls les dix premiers d'entre eux sont utilisés (0000 à 1001). Les six combinaisons de codes restantes, c'est-à-dire 1010 à 1111, ne sont pas valides en BCD.
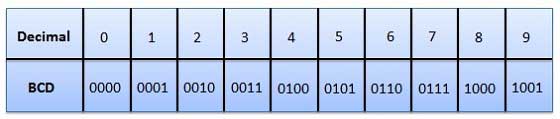
Avantages des codes BCD
- Il est très similaire au système décimal.
- Nous devons nous souvenir de l'équivalent binaire des nombres décimaux de 0 à 9 uniquement.
Inconvénients des codes BCD
L'addition et la soustraction de BCD ont des règles différentes.
L'arithmétique BCD est un peu plus compliquée.
BCD a besoin de plus de bits que de binaires pour représenter le nombre décimal. Le BCD est donc moins efficace que le binaire.
Codes alphanumériques
Un chiffre ou un bit binaire ne peut représenter que deux symboles car il n'a que deux états «0» ou «1». Mais cela ne suffit pas pour la communication entre deux ordinateurs car nous avons besoin de beaucoup plus de symboles pour la communication. Ces symboles doivent représenter 26 alphabets avec des majuscules et des minuscules, des chiffres de 0 à 9, des signes de ponctuation et d'autres symboles.
Les codes alphanumériques sont les codes qui représentent des nombres et des caractères alphabétiques. La plupart du temps, ces codes représentent également d'autres caractères tels que des symboles et diverses instructions nécessaires pour transmettre des informations. Un code alphanumérique doit au moins représenter 10 chiffres et 26 lettres de l'alphabet, soit un total de 36 éléments. Les trois codes alphanumériques suivants sont très couramment utilisés pour la représentation des données.
- Code standard américain pour l'échange d'informations (ASCII).
- Code d'échange décimal codé binaire étendu (EBCDIC).
- Code Baudot à cinq bits.
Le code ASCII est un code 7 bits tandis que EBCDIC est un code 8 bits. Le code ASCII est plus couramment utilisé dans le monde, tandis que EBCDIC est principalement utilisé dans les gros ordinateurs IBM.
Codes d'erreur
Il existe des techniques de code binaire pour détecter et corriger les données pendant la transmission de données.
| Code d'erreur | La description |
|---|---|
Détection et correction des erreurs |
Techniques de détection d'erreur et de code de correction |
Il existe de nombreuses méthodes ou techniques qui peuvent être utilisées pour convertir du code d'un format à un autre. Nous allons démontrer ici ce qui suit
- Conversion binaire en BCD
- Conversion BCD en binaire
- BCD à Excess-3
- Excès-3 au BCD
Conversion binaire en BCD
Pas
Step 1 - Convertissez le nombre binaire en nombre décimal.
Step 2 - Convertissez le nombre décimal en BCD.
Exemple - convertissez (11101) 2 en BCD.
Étape 1 - Convertir en décimal
Nombre binaire - 11101 2
Calcul de l'équivalent décimal -
| Étape | Nombre binaire | Nombre décimal |
|---|---|---|
| Étape 1 | 11101 2 | ((1 × 2 4 ) + (1 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 )) 10 |
| Étape 2 | 11101 2 | (16 + 8 + 4 + 0 + 1) 10 |
| Étape 3 | 11101 2 | 29 10 |
Nombre binaire - 11101 2 = Nombre décimal - 29 10
Étape 2 - Convertir en BCD
Nombre décimal - 29 10
Calcul de l'équivalent BCD. Convertissez chaque chiffre en groupes de quatre chiffres binaires équivalents.
| Étape | Nombre décimal | Conversion |
|---|---|---|
| Étape 1 | 29 10 | 0010 2 1001 2 |
| Étape 2 | 29 10 | 00101001 BCD |
Résultat
(11101)2 = (00101001)BCDConversion BCD en binaire
Pas
Step 1 - Convertissez le nombre BCD en décimal.
Step 2 - Conversion décimale en binaire.
Exemple - convertir (00101001) BCD en binaire.
Étape 1 - Convertir en BCD
Numéro BCD - (00101001) BCD
Calcul de l'équivalent décimal. Convertissez chaque quatre chiffres en un groupe et obtenez l'équivalent décimal pour chaque groupe.
| Étape | Numéro BCD | Conversion |
|---|---|---|
| Étape 1 | (00101001) BCD | 0010 2 1001 2 |
| Étape 2 | (00101001) BCD | 2 10 9 10 |
| Étape 3 | (00101001) BCD | 29 10 |
Numéro BCD - (00101001) BCD = Nombre décimal - 29 10
Étape 2 - Convertir en binaire
Méthode de division longue utilisée pour la conversion décimale en binaire.
Nombre décimal - 29 10
Calcul de l'équivalent binaire -
| Étape | Opération | Résultat | Reste |
|---|---|---|---|
| Étape 1 | 29/2 | 14 | 1 |
| Étape 2 | 14/2 | sept | 0 |
| Étape 3 | 7/2 | 3 | 1 |
| Étape 4 | 3/2 | 1 | 1 |
| Étape 5 | 1/2 | 0 | 1 |
Comme mentionné aux étapes 2 et 4, les restes doivent être disposés dans l'ordre inverse de sorte que le premier reste devienne le chiffre le moins significatif (LSD) et le dernier reste le chiffre le plus significatif (MSD).
Nombre décimal - 29 10 = Nombre binaire - 11101 2
Résultat
(00101001)BCD = (11101)2BCD à Excess-3
Pas
Step 1 - Convertissez BCD en décimal.
Step 2- Ajoutez (3) 10 à ce nombre décimal.
Step 3 - Convertissez en binaire pour obtenir du code en excès-3.
Exemple - convertissez (0110) BCD en Excess-3.
Étape 1 - Convertir en décimal
(0110) BCD = 6 10
Étape 2 - Ajouter 3 à la décimale
(6) 10 + (3) 10 = (9) 10
Étape 3 - Convertir en Excess-3
(9) 10 = (1001) 2
Résultat
(0110)BCD = (1001)XS-3Conversion Excess-3 en BCD
Pas
Step 1- Soustraire (0011) 2 de chaque 4 bits de 3 chiffres en excès pour obtenir le code BCD correspondant.
Exemple - convertir (10011010) XS-3 en BCD.
Given XS-3 number = 1 0 0 1 1 0 1 0
Subtract (0011)2 = 1 0 0 1 0 1 1 1
--------------------
BCD = 0 1 1 0 0 1 1 1Résultat
(10011010)XS-3 = (01100111)BCDDes compléments sont utilisés dans les calculateurs numériques afin de simplifier l'opération de soustraction et pour les manipulations logiques. Pour chaque système radix-r (radix r représente la base du système numérique), il existe deux types de compléments.
| SN | Complément | La description |
|---|---|---|
| 1 | Complément Radix | Le complément de base est appelé complément du r |
| 2 | Complément Radix diminué | Le complément radix diminué est appelé complément de (r-1) |
Compléments du système binaire
Comme le système binaire a une base r = 2. Ainsi, les deux types de compléments pour le système binaire sont le complément à 2 et le complément à 1.
Complément 1
Le complément 1 d'un nombre est trouvé en changeant tous les 1 en 0 et tous les 0 en 1. C'est ce qu'on appelle prendre le complément ou le complément de 1. Un exemple de complément à 1 est le suivant.
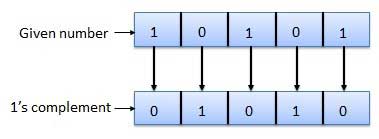
Complément de 2
Le complément du nombre binaire à 2 est obtenu en ajoutant 1 au bit le moins significatif (LSB) du complément à 1 du nombre.
Complément à 2 = complément à 1 + 1
Un exemple de complément à 2 est le suivant.
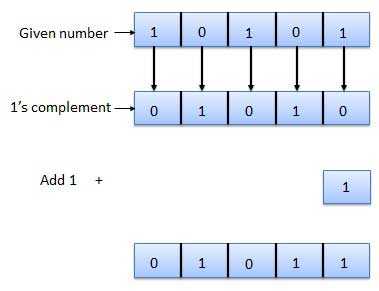
L'arithmétique binaire est une partie essentielle de tous les ordinateurs numériques et de nombreux autres systèmes numériques.
Addition binaire
C'est une clé pour la soustraction binaire, la multiplication, la division. Il existe quatre règles d'addition binaire.
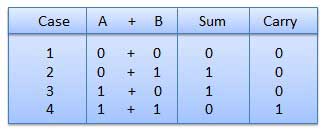
Dans le quatrième cas, une addition binaire crée une somme de (1 + 1 = 10) c'est-à-dire que 0 est écrit dans la colonne donnée et un report de 1 à la colonne suivante.
Exemple - Ajout
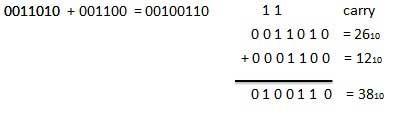
Soustraction binaire
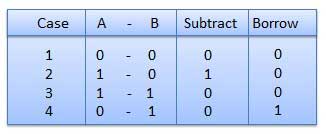
Subtraction and Borrow, ces deux mots seront très fréquemment utilisés pour la soustraction binaire. Il existe quatre règles de soustraction binaire.
Exemple - Soustraction
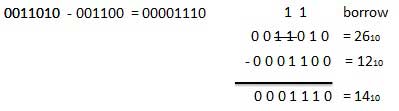
Multiplication binaire
La multiplication binaire est similaire à la multiplication décimale. C'est plus simple que la multiplication décimale car seuls les 0 et les 1 sont impliqués. Il existe quatre règles de multiplication binaire.
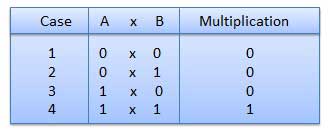
Exemple - Multiplication

Division binaire
La division binaire est similaire à la division décimale. C'est ce qu'on appelle la procédure de division longue.
Exemple - Division

Système de nombre octal
Voici les caractéristiques d'un système de nombres octaux.
Utilise huit chiffres, 0,1,2,3,4,5,6,7.
Aussi appelé système numérique de base 8.
Chaque position dans un nombre octal représente une puissance 0 de la base (8). Exemple: 8 0
La dernière position dans un nombre octal représente une puissance x de la base (8). Exemple: 8 x où x représente la dernière position - 1.
Exemple
Numéro octal - 12570 8
Calcul de l'équivalent décimal -
| Étape | Numéro octal | Nombre décimal |
|---|---|---|
| Étape 1 | 12570 8 | ((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10 |
| Étape 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| Étape 3 | 12570 8 | 5496 10 |
Note −12570 8 s'écrit normalement 12570.
Addition octale
Le tableau suivant d'addition octale vous aidera à gérer l'addition octale.

Pour utiliser ce tableau, suivez simplement les instructions utilisées dans cet exemple: Ajoutez 6 8 et 5 8 . Localisez 6 dans la colonne A, puis recherchez le 5 dans la colonne B. Le point dans la zone «somme» où ces deux colonnes se croisent est la «somme» de deux nombres.
68 + 58 = 138.Exemple - Ajout
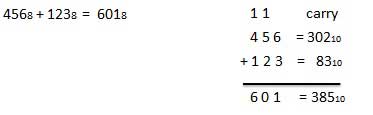
Soustraction octale
La soustraction des nombres octaux suit les mêmes règles que la soustraction des nombres dans tout autre système numérique. La seule variation est le nombre emprunté. Dans le système décimal, vous empruntez un groupe de 10 10 . Dans le système binaire, vous empruntez un groupe de 2 10 . Dans le système octal, vous empruntez un groupe de 8 10 .
Exemple - Soustraction
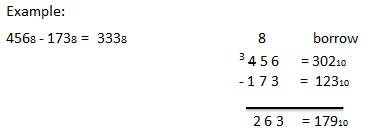
Système de nombres hexadécimaux
Voici les caractéristiques d'un système de nombres hexadécimaux.
Utilise 10 chiffres et 6 lettres, 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F.
Les lettres représentent des nombres commençant à 10. A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Aussi appelé système de numérotation de base 16.
Chaque position dans un nombre hexadécimal représente une puissance 0 de la base (16). Exemple - 16 0
La dernière position dans un nombre hexadécimal représente une puissance x de la base (16). Exemple - 16 x où x représente la dernière position - 1.
Exemple
Nombre hexadécimal - 19FDE 16
Calcul de l'équivalent décimal -
| Étape | Nombre hexadécimal | Nombre décimal |
|---|---|---|
| Étape 1 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (F × 16 2 ) + (D × 16 1 ) + (E × 16 0 )) 10 |
| Étape 2 | 19FDE 16 | ((1 × 16 4 ) + (9 × 16 3 ) + (15 × 16 2 ) + (13 × 16 1 ) + (14 × 16 0 )) 10 |
| Étape 3 | 19FDE 16 | (65536 + 36864 + 3840 + 208 + 14) 10 |
| Étape 4 | 19FDE 16 | 106462 10 |
Note −19FDE 16 s'écrit normalement 19FDE.
Addition hexadécimale
Le tableau d'addition hexadécimal suivant vous aidera grandement à gérer l'addition hexadécimale.
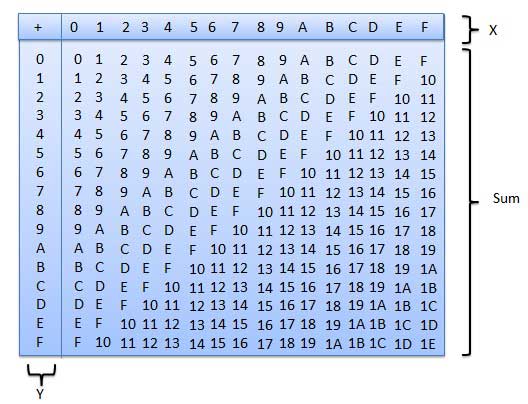
Pour utiliser ce tableau, suivez simplement les instructions utilisées dans cet exemple - Ajouter A 16 et 5 16 . Localisez A dans la colonne X, puis recherchez le 5 dans la colonne Y. Le point dans la zone «somme» où ces deux colonnes se croisent est la somme de deux nombres.
A16 + 516 = F16.Exemple - Ajout
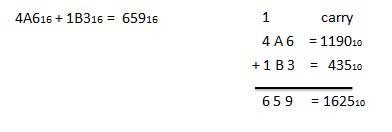
Soustraction hexadécimale
La soustraction de nombres hexadécimaux suit les mêmes règles que la soustraction de nombres dans tout autre système de nombres. La seule variation est le nombre emprunté. Dans le système décimal, vous empruntez un groupe de 10 10 . Dans le système binaire, vous empruntez un groupe de 2 10 . Dans le système hexadécimal, vous empruntez un groupe de 16 10 .
Exemple - Soustraction

L'algèbre booléenne est utilisée pour analyser et simplifier les circuits numériques (logiques). Il utilise uniquement les nombres binaires, c'est-à-dire 0 et 1. Il est également appeléBinary Algebra ou logical Algebra. L'algèbre booléenne a été inventée parGeorge Boole en 1854.
Règle en algèbre booléenne
Voici les règles importantes utilisées en algèbre booléenne.
La variable utilisée ne peut avoir que deux valeurs. Binaire 1 pour HIGH et Binary 0 pour LOW.
Le complément d'une variable est représenté par un overbar (-). Ainsi, le complément de la variable B est représenté par
. Ainsi si B = 0 alors = 1 et B = 1 alors
= 1 et B = 1 alors = 0.
= 0.
ORing des variables est représenté par un signe plus (+) entre elles. Par exemple, ORing de A, B, C est représenté par A + B + C.
Le AND logique des deux variables ou plus est représenté par l'écriture d'un point entre eux, tel que ABC Parfois, le point peut être omis comme ABC.
Lois booléennes
Il existe six types de lois booléennes.
Loi commutative
Toute opération binaire qui satisfait l'expression suivante est appelée opération commutative.

La loi commutative stipule que la modification de la séquence des variables n'a aucun effet sur la sortie d'un circuit logique.
Droit associatif
Cette loi stipule que l'ordre dans lequel les opérations logiques sont effectuées n'est pas pertinent car leur effet est le même.
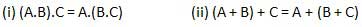
Loi distributive
La loi distributive énonce la condition suivante.
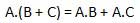
ET loi
Ces lois utilisent l'opération ET. Par conséquent, ils sont appelés commeAND lois.
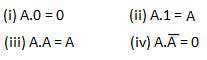
OU loi
Ces lois utilisent l'opération OR. Par conséquent, ils sont appelés commeOR lois.
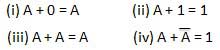
Loi INVERSION
Cette loi utilise l'opération NOT. La loi d'inversion stipule que la double inversion d'une variable entraîne la variable d'origine elle-même.
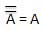
Théorèmes booléens importants
Voici quelques théorèmes booléens importants.
| Fonction booléenne / théorèmes | La description |
|---|---|
Fonctions booléennes |
Fonctions et expressions booléennes, réalisation de portes K-Map et NAND |
Théorèmes de De Morgan |
Théorème 1 et Théorème 2 de De Morgan |
Les portes logiques sont les éléments de base de tout système numérique. C'est un circuit électronique ayant une ou plusieurs entrées et une seule sortie. La relation entre l'entrée et la sortie est basée sur uncertain logic. Sur cette base, les portes logiques sont nommées porte ET, porte OU, porte NON, etc.
ET Porte
Un circuit qui effectue une opération ET est illustré sur la figure. Il a n entrée (n> = 2) et une sortie.

Diagramme logique
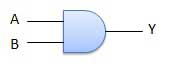
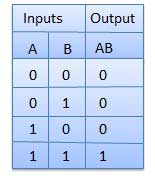
Table de vérité
OU Porte
Un circuit qui effectue une opération OU est illustré sur la figure. Il a n entrée (n> = 2) et une sortie.
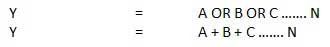
Diagramme logique
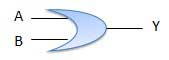
Table de vérité
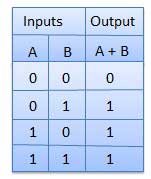
PAS de porte
La porte NOT est également connue sous le nom Inverter. Il a une entrée A et une sortie Y.
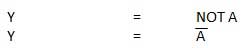
Diagramme logique
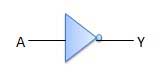
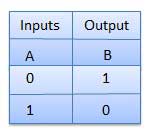
Table de vérité
Porte NAND
Une opération NOT-AND est appelée opération NAND. Il a n entrée (n> = 2) et une sortie.
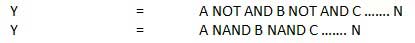
Diagramme logique
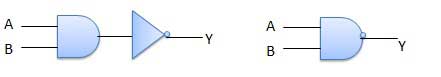
Table de vérité
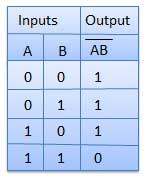
Porte NOR
Une opération NOT-OR est appelée opération NOR. Il a n entrée (n> = 2) et une sortie.
Diagramme logique
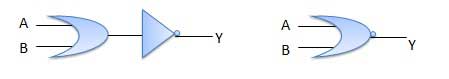
Table de vérité
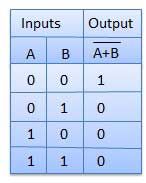
Porte XOR
La porte XOR ou Ex-OR est un type spécial de porte. Il peut être utilisé dans le demi-additionneur, l'additionneur complet et le soustracteur. La porte OU exclusif est abrégée en porte EX-OU ou parfois en porte X-OR. Il a n entrée (n> = 2) et une sortie.
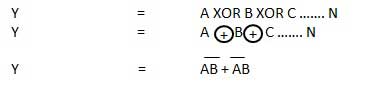
Diagramme logique
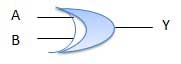
Table de vérité
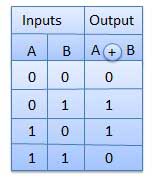
Porte XNOR
La porte XNOR est un type spécial de porte. Il peut être utilisé dans le demi-additionneur, l'additionneur complet et le soustracteur. La porte exclusive-NOR est abrégée en porte EX-NOR ou parfois en porte X-NOR. Il a n entrée (n> = 2) et une sortie.
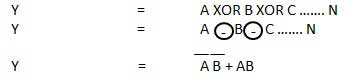
Diagramme logique
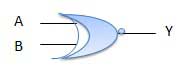
Table de vérité
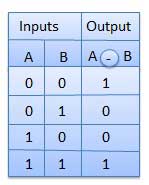
Le circuit combinatoire est un circuit dans lequel nous combinons les différentes portes du circuit, par exemple codeur, décodeur, multiplexeur et démultiplexeur. Certaines des caractéristiques des circuits combinatoires sont les suivantes:
La sortie du circuit combinatoire à tout instant de temps, ne dépend que des niveaux présents aux bornes d'entrée.
Le circuit combinatoire n'utilise aucune mémoire. L'état d'entrée précédent n'a aucun effet sur l'état actuel du circuit.
Un circuit combinatoire peut avoir un nombre n d'entrées et m nombre de sorties.
Diagramme
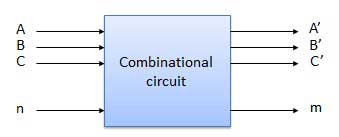
Nous allons élaborer quelques circuits combinatoires importants comme suit.
Demi-additionneur
Le demi-additionneur est un circuit logique combinatoire avec deux entrées et deux sorties. Le circuit de demi-additionneur est conçu pour ajouter deux nombres binaires A et B à un seul bit.C'est le bloc de base pour l'ajout de deuxsinglenuméros de bits. Ce circuit a deux sortiescarry et sum.
Diagramme

Table de vérité
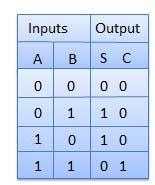
Schéma
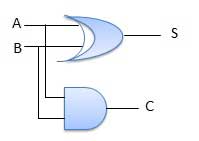
Additionneur complet
L'additionneur complet est développé pour surmonter l'inconvénient du circuit Half Adder. Il peut ajouter deux nombres A et B d'un bit et porter c. L'additionneur complet est un circuit combinatoire à trois entrées et deux sorties.
Diagramme

Table de vérité
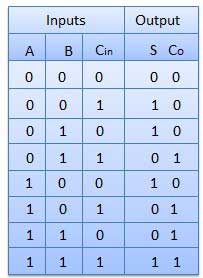
Schéma
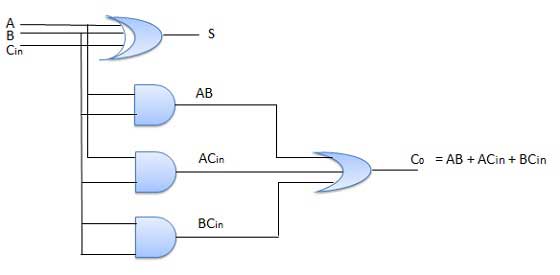
Additionneur parallèle N-Bit
Le Full Adder est capable d'ajouter seulement deux nombres binaires à un seul chiffre avec une entrée de retenue. Mais en pratique, nous devons ajouter des nombres binaires qui sont beaucoup plus longs qu'un seul bit. Pour ajouter deux nombres binaires à n bits, nous devons utiliser l'additionneur parallèle à n bits. Il utilise un certain nombre d'additionneurs complets en cascade. La sortie de report de l'additionneur complet précédent est connectée pour transporter l'entrée de l'additionneur complet suivant.
Additionneur parallèle 4 bits
Dans le schéma fonctionnel, A 0 et B 0 représentent le LSB des mots de quatre bits A et B. Par conséquent, le Full Adder-0 est le niveau le plus bas. Par conséquent, son C in a été rendu en permanence à 0. Le reste des connexions sont exactement les mêmes que celles de l'additionneur parallèle à n bits est représenté sur la fig. L'additionneur parallèle à quatre bits est un circuit logique très courant.
Diagramme

Soustracteur parallèle N-Bit
La soustraction peut être effectuée en prenant le complément 1 ou 2 du nombre à soustraire. Par exemple, nous pouvons effectuer la soustraction (AB) en ajoutant le complément 1 ou 2 de B à A. Cela signifie que nous pouvons utiliser un additionneur binaire pour effectuer la soustraction binaire.
Soustracteur parallèle 4 bits
Le nombre à soustraire (B) est d'abord passé par les onduleurs pour obtenir son complément à 1. L'additionneur de 4 bits ajoute ensuite le complément A et 2 de B pour produire la soustraction. S 3 S 2 S 1 S 0 représente le résultat de la soustraction binaire (AB) et la sortie de report C out représente la polarité du résultat. Si A> B alors Cout = 0 et le résultat de la forme binaire (AB) alors C out = 1 et le résultat est sous la forme du complément à 2.
Diagramme
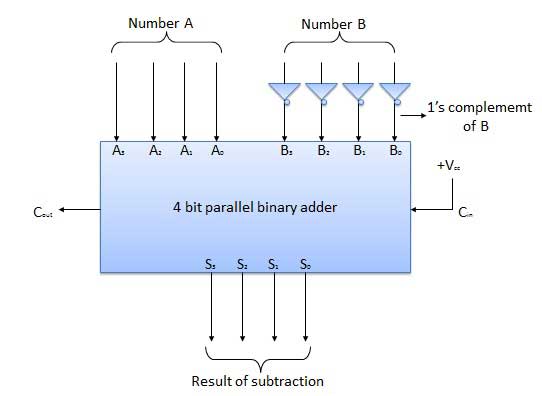
Demi soustracteurs
Le demi-soustracteur est un circuit combiné avec deux entrées et deux sorties (différence et emprunt). Il produit la différence entre les deux bits binaires en entrée et produit également une sortie (Borrow) pour indiquer si un 1 a été emprunté. Dans la soustraction (AB), A est appelé bit Minuend et B est appelé bit Subtrahend.
Table de vérité
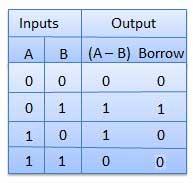
Schéma
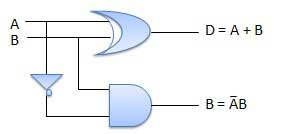
Soustracteurs complets
L'inconvénient d'un demi soustracteur est surmonté par un soustracteur complet. Le soustracteur complet est un circuit combinatoire avec trois entrées A, B, C et deux sorties D et C '. A est le «minuend», B est «subtrahend», C est le «emprunt» produit par l'étape précédente, D est la sortie de différence et C 'est la sortie de l'emprunt.
Table de vérité
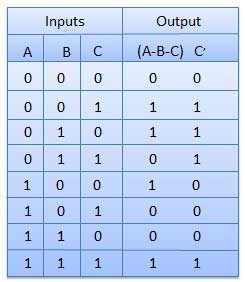
Schéma
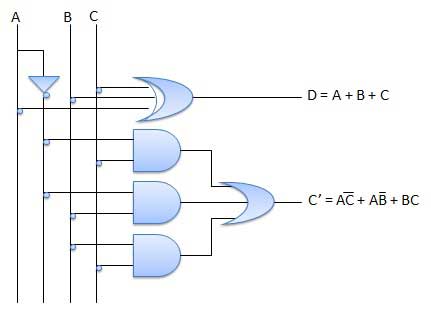
Multiplexeurs
Le multiplexeur est un type spécial de circuit combinatoire. Il existe n entrées de données, une sortie et m entrées de sélection avec 2m = n. C'est un circuit numérique qui sélectionne l'une des n entrées de données et l'achemine vers la sortie. La sélection de l'une des n entrées se fait par les entrées sélectionnées. En fonction du code numérique appliqué aux entrées sélectionnées, une source de données sur n est sélectionnée et transmise à la sortie unique Y. E est appelée entrée stroboscopique ou d'activation qui est utile pour la mise en cascade. Il s'agit généralement d'un terminal bas actif, ce qui signifie qu'il effectuera l'opération requise lorsqu'il est bas.
Diagramme
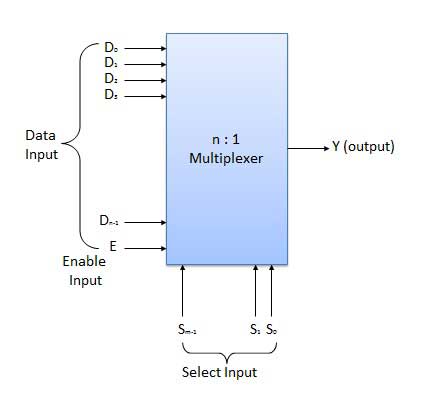
Les multiplexeurs sont disponibles en plusieurs variantes
- Multiplexeur 2: 1
- Multiplexeur 4: 1
- Multiplexeur 16: 1
- Multiplexeur 32: 1
Diagramme
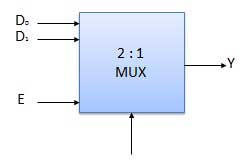
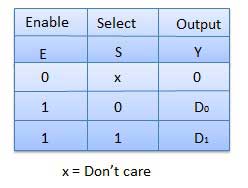
Table de vérité
Démultiplexeurs
Un démultiplexeur effectue l'opération inverse d'un multiplexeur c'est-à-dire qu'il reçoit une entrée et la distribue sur plusieurs sorties. Il n'a qu'une seule entrée, n sorties, m sélection d'entrée. À la fois, une seule ligne de sortie est sélectionnée par les lignes de sélection et l'entrée est transmise à la ligne de sortie sélectionnée. Un démultiplexeur équivaut à un interrupteur multipolaire unipolaire comme illustré à la fig.
Les démultiplexeurs sont disponibles en plusieurs variantes.
- Démultiplexeur 1: 2
- Démultiplexeur 1: 4
- Démultiplexeur 1: 16
- Démultiplexeur 1:32
Diagramme
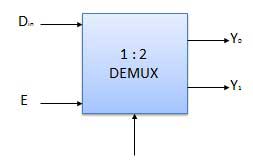
Table de vérité
Décodeur
Un décodeur est un circuit combinatoire. Il a n entrées et au maximum m = 2n sorties. Le décodeur est identique à un démultiplexeur sans aucune entrée de données. Il effectue des opérations exactement opposées à celles d'un codeur.
Diagramme

Voici des exemples de décodeurs.
- Convertisseurs de code
- Décodeurs BCD à sept segments
- Décodeurs à tube Nixie
- Actionneur de relais
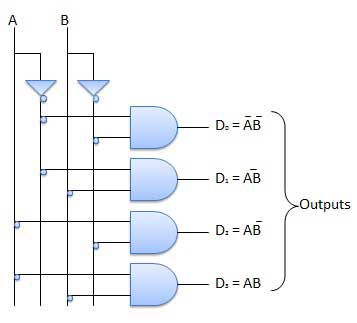
Décodeur 2 à 4 lignes
Le schéma synoptique du décodeur 2 à 4 lignes est illustré à la fig. A et B sont les deux entrées où D à D sont les quatre sorties. La table de vérité explique les opérations d'un décodeur. Il montre que chaque sortie est 1 pour une seule combinaison spécifique d'entrées.
Diagramme

Table de vérité

Circuit logique
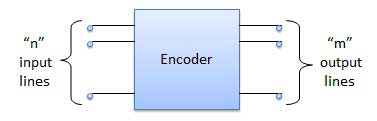
Encodeur
Le codeur est un circuit combinatoire conçu pour effectuer l'opération inverse du décodeur. Un encodeur a n nombre de lignes d'entrée et m nombre de lignes de sortie. Un codeur produit un code binaire à m bits correspondant au numéro d'entrée numérique. Le codeur accepte un mot numérique d'entrée à n et le convertit en un mot numérique de m bit.
Diagramme
Voici des exemples d'encodeurs.
- Codeurs prioritaires
- Encodeur décimal à BCD
- Codeur octal à binaire
- Codeur hexadécimal à binaire
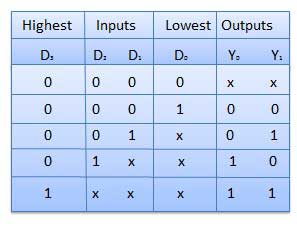
Encodeur prioritaire
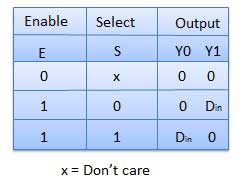
Il s'agit d'un type d'encodeur spécial. La priorité est donnée aux lignes d'entrée. Si deux lignes d'entrée ou plus sont égales à 1 en même temps, la ligne d'entrée avec la priorité la plus élevée sera prise en compte. Il y a quatre entrées D 0 , D 1 , D 2 , D 3 et deux sorties Y 0 , Y 1 . Sur les quatre entrées, D 3 a la priorité la plus élevée et D 0 a la priorité la plus basse. Cela signifie que si D 3 = 1 alors Y 1 Y 1 = 11 quelles que soient les autres entrées. De même si D 3 = 0 et D 2 = 1 alors Y 1 Y 0 = 10 indépendamment des autres entrées.
Diagramme

Table de vérité
Circuit logique
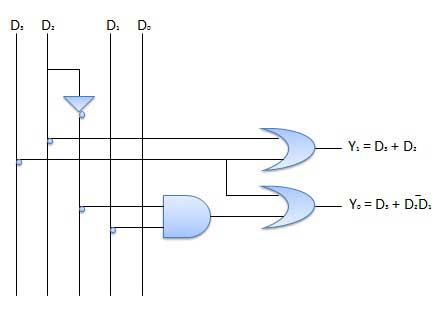
Le circuit combinatoire n'utilise aucune mémoire. Par conséquent, l'état antérieur de l'entrée n'a aucun effet sur l'état actuel du circuit. Mais le circuit séquentiel a une mémoire, donc la sortie peut varier en fonction de l'entrée. Ce type de circuits utilise une entrée, une sortie, une horloge et un élément de mémoire précédents.
Diagramme
Tongues
La bascule est un circuit séquentiel qui échantillonne généralement ses entrées et ne modifie ses sorties qu'à des instants de temps particuliers et non en continu. On dit que la bascule est sensible aux bords ou déclenchée par les bords plutôt que d'être déclenchée au niveau comme des verrous.
Flip Flop SR
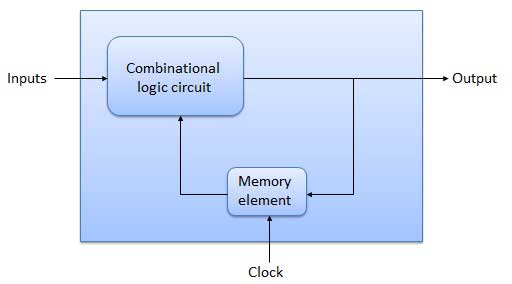
Il s'agit essentiellement d'un verrou SR utilisant des portes NAND avec un enablecontribution. Il est également appelé SR-FF déclenché par niveau. Pour cela, le circuit en sortie aura lieu si et seulement si l'entrée de validation (E) est rendue active. En bref, ce circuit fonctionnera comme un verrou SR si E = 1 mais il n'y a pas de changement dans la sortie si E = 0.
Diagramme
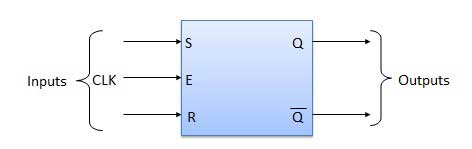
Schéma
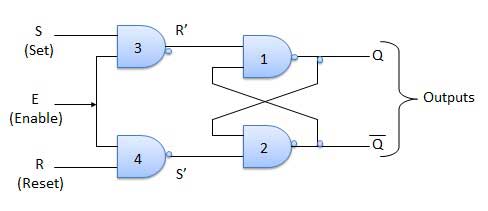
Table de vérité
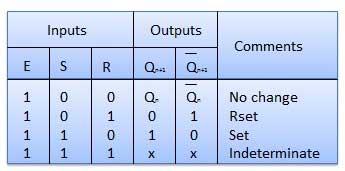
Opération
| SN | État | Opération |
|---|---|---|
| 1 | S = R = 0 : No change | Si S = R = 0, la sortie des portes NAND 3 et 4 est forcée de devenir 1. Par conséquent, R 'et S' seront tous deux égaux à 1. Puisque S 'et R' sont l'entrée du verrou SR de base utilisant des portes NAND, il n'y aura pas de changement dans l'état des sorties. |
| 2 | S = 0, R = 1, E = 1 | Puisque S = 0, la sortie de NAND-3 c'est-à-dire R '= 1 et E = 1 la sortie de NAND-4 c'est-à-dire S' = 0. D'où Q n + 1 = 0 et Q n + 1 bar = 1. Il s'agit d'une condition de réinitialisation. |
| 3 | S = 1, R = 0, E = 1 | Sortie de NAND-3 c'est-à-dire R '= 0 et sortie de NAND-4 soit S' = 1. Par conséquent, la sortie du verrou SR NAND est Q n + 1 = 1 et Q n + 1 bar = 0. Il s'agit de la condition de réinitialisation. |
| 4 | S = 1, R = 1, E = 1 | Comme S = 1, R = 1 et E = 1, la sortie des portes NAND 3 et 4 est toutes deux 0, c'est-à-dire que S '= R' = 0. D'où le Race condition se produira dans le verrou NAND de base. |
Bascule maître esclave JK
Le maître esclave JK FF est une cascade de deux SR FF avec retour de la sortie du second vers l'entrée du premier. Master est un niveau positif déclenché. Mais en raison de la présence de l'onduleur dans la ligne d'horloge, l'esclave répondra au niveau négatif. Par conséquent, lorsque l'horloge = 1 (niveau positif), le maître est actif et l'esclave est inactif. Alors que quand horloge = 0 (niveau bas), l'esclave est actif et le maître est inactif.
Schéma
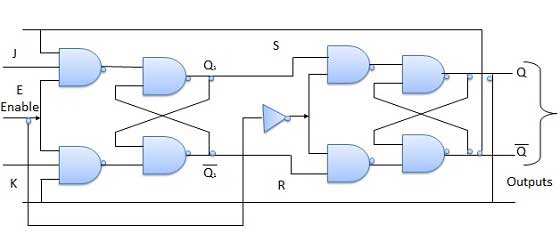
Table de vérité
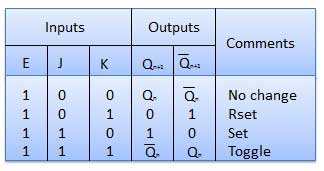
Opération
| SN | État | Opération |
|---|---|---|
| 1 | J = K = 0 (No change) | Lorsque clock = 0, l'esclave devient actif et le maître est inactif. Mais comme les entrées S et R n'ont pas changé, les sorties esclaves resteront également inchangées. Par conséquent, les sorties ne changeront pas si J = K = 0. |
| 2 | J = 0 and K = 1 (Reset) | Horloge = 1 - Maître actif, esclave inactif. Par conséquent, les sorties du maître deviennent Q 1 = 0 et Q 1 bar = 1. Cela signifie S = 0 et R = 1. Horloge = 0 - Esclave actif, maître inactif. Par conséquent, les sorties de l'esclave deviennent Q = 0 et Q bar = 1. Encore une fois horloge = 1 - Maître actif, esclave inactif. Par conséquent, même avec les sorties modifiées Q = 0 et Q bar = 1 renvoyées au maître, sa sortie sera Q1 = 0 et Q1 bar = 1. Cela signifie S = 0 et R = 1. Par conséquent, avec horloge = 0 et esclave devenant actif, les sorties de l'esclave resteront Q = 0 et Q bar = 1. Ainsi, nous obtenons une sortie stable du maître esclave. |
| 3 | J = 1 and K = 0 (Set) | Horloge = 1 - Maître actif, esclave inactif. Par conséquent, les sorties du maître deviennent Q 1 = 1 et Q 1 bar = 0. Cela signifie S = 1 et R = 0. Horloge = 0 - Esclave actif, maître inactif. Par conséquent, les sorties de l'esclave deviennent Q = 1 et Q bar = 0. Encore une fois clock = 1 - alors on peut montrer que les sorties de l'esclave sont stabilisées à Q = 1 et Q bar = 0. |
| 4 | J = K = 1 (Toggle) | Horloge = 1 - Maître actif, esclave inactif. Les sorties du maître basculeront. Ainsi, S et R seront également inversés. Horloge = 0 - Esclave actif, maître inactif. Les sorties de l'esclave basculeront. Ces sorties modifiées sont renvoyées aux entrées principales. Mais puisque clock = 0, le maître est toujours inactif. Il ne répond donc pas à ces sorties modifiées. Cela évite le basculement multiple qui conduit à la condition de course autour. La bascule maître esclave évitera la condition de contournement. |
Retard Flip Flop / D Flip Flop
Delay Flip Flop ou D Flip Flop est le verrou SR à déclenchement simple avec un inverseur NAND connecté entre les entrées S et R. Il n'a qu'une seule entrée. Les données d'entrée apparaissent à la sortie après un certain temps. En raison de ce retard de données entre i / p et o / p, il est appelé flip flop de retard. S et R seront les compléments l'un de l'autre en raison de l'inverseur NAND. Donc S = R = 0 ou S = R = 1, ces conditions d'entrée n'apparaîtront jamais. Ce problème est évité par les conditions SR = 00 et SR = 1.
Diagramme
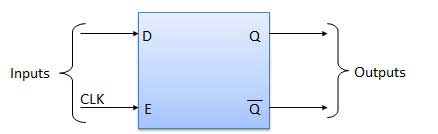
Schéma
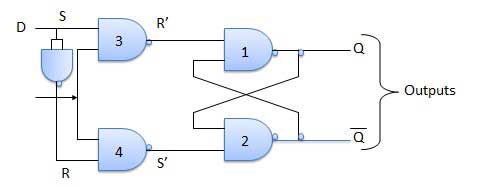
Table de vérité
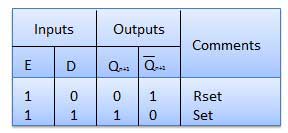
Opération
| SN | État | Opération |
|---|---|---|
| 1 | E = 0 | Le verrou est désactivé. Donc pas de changement dans la production. |
| 2 | E = 1 and D = 0 | Si E = 1 et D = 0 alors S = 0 et R = 1. Ainsi, quel que soit l'état actuel, l'état suivant est Q n + 1 = 0 et Q n + 1 bar = 1. C'est la condition de réinitialisation. |
| 3 | E = 1 and D = 1 | Si E = 1 et D = 1, alors S = 1 et R = 0. Cela définira le verrou et Q n + 1 = 1 et Q n + 1 bar = 0 quel que soit l'état actuel. |
Basculer Flip Flop / T Flip Flop
Bascule bascule est essentiellement une bascule JK avec des bornes J et K connectées en permanence ensemble. Il n'a qu'une entrée désignée parTcomme indiqué dans le diagramme des symboles. Le symbole de la bascule T déclenchée par front positif est indiqué dans le diagramme.
Diagramme de symboles
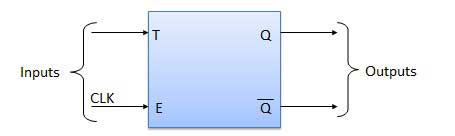
Diagramme
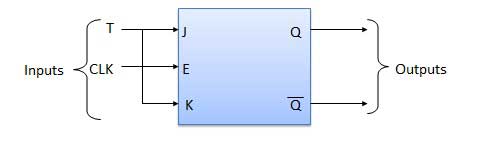
Table de vérité
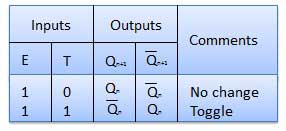
Opération
| SN | État | Opération |
|---|---|---|
| 1 | T = 0, J = K = 0 | Les barres Q et Q de sortie ne changeront pas |
| 2 | T = 1, J = K = 1 | La sortie bascule en fonction de chaque front montant du signal d'horloge. |
La bascule est une cellule de mémoire 1 bit qui peut être utilisée pour stocker les données numériques. Pour augmenter la capacité de stockage en termes de nombre de bits, il faut utiliser un groupe de bascules. Un tel groupe de bascules est connu comme unRegister. len-bit register se composera de n nombre de bascules et il est capable de stocker un n-bit mot.
Les données binaires d'un registre peuvent être déplacées à l'intérieur du registre d'une bascule à une autre. Les registres qui permettent de tels transferts de données sont appelésshift registers. Il existe quatre modes de fonctionnement d'un registre à décalage.
- Entrée série Sortie série
- Entrée série Sortie parallèle
- Entrée parallèle Sortie série
- Entrée parallèle Sortie parallèle
Entrée série Sortie série
Que toutes les bascules soient initialement dans la condition de réinitialisation, c'est-à-dire Q 3 = Q 2 = Q 1 = Q 0 = 0. Si une entrée d'un nombre binaire de quatre bits 1 1 1 1 est faite dans le registre, ce nombre doit être appliqué àDinbit avec le bit LSB appliqué en premier. L'entrée D de FF-3 c'est-à-dire D 3 est connectée à l'entrée de données sérieDin. La sortie de FF-3, c'est-à-dire Q 3, est connectée à l'entrée de la bascule suivante, c'est-à-dire D 2 et ainsi de suite.
Diagramme
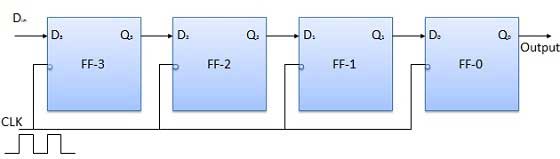
Opération
Avant l'application du signal d'horloge, laissez Q 3 Q 2 Q 1 Q 0 = 0000 et appliquez le bit LSB du nombre à entrer dans D in . Donc D in = D 3 = 1. Appliquez l'horloge. Sur le premier front descendant de l'horloge, le FF-3 est mis à 1 et le mot stocké dans le registre est Q 3 Q 2 Q 1 Q 0 = 1000.
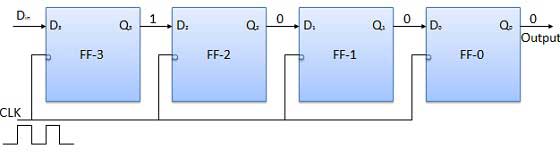
Appliquez le bit suivant à D dans . Donc D in = 1. Dès que le prochain front négatif de l'horloge arrive, FF-2 sera mis à 1 et le mot stocké changera en Q 3 Q 2 Q 1 Q 0 = 1100.
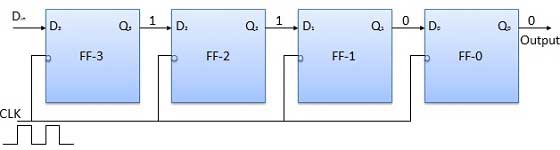
Appliquer le bit suivant à stocker, c'est-à-dire 1 à D dans . Appliquez l'impulsion d'horloge. Dès que le troisième front d'horloge négatif atteint, FF-1 sera établi et la sortie sera modifiée en Q 3 Q 2 Q 1 Q 0 = 1110.
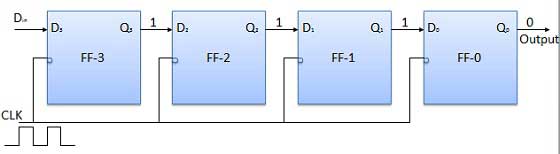
De même avec D in = 1 et avec l'arrivée du quatrième front d'horloge négatif, le mot stocké dans le registre est Q 3 Q 2 Q 1 Q 0 = 1111.
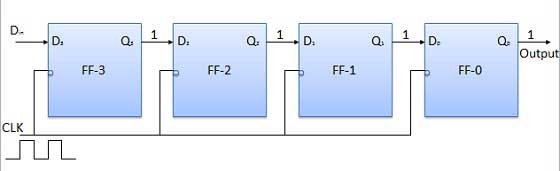
Table de vérité
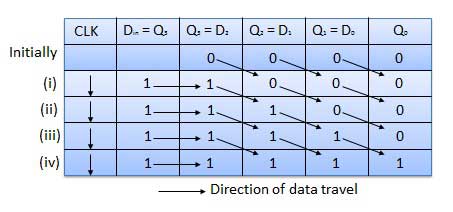
Formes d'onde

Entrée série Sortie parallèle
Dans de tels types d'opérations, les données sont saisies en série et extraites de manière parallèle.
Les données sont chargées petit à petit. Les sorties sont désactivées tant que les données sont en cours de chargement.
Dès que le chargement des données est terminé, toutes les bascules contiennent les données requises, les sorties sont activées de sorte que toutes les données chargées sont rendues disponibles sur toutes les lignes de sortie en même temps.
4 cycles d'horloge sont nécessaires pour charger un mot de quatre bits. Par conséquent, la vitesse de fonctionnement du mode SIPO est la même que celle du mode SISO.
Diagramme
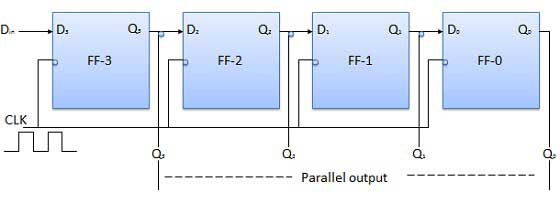
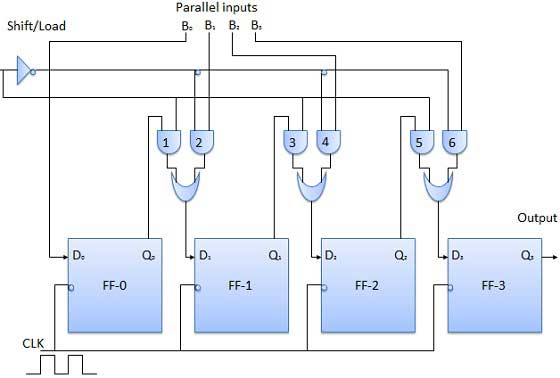
Sortie série d'entrée parallèle (PISO)
Les bits de données sont entrés en parallèle.
Le circuit illustré ci-dessous est un registre de sortie série d'entrée parallèle à quatre bits.
La sortie de la bascule précédente est connectée à l'entrée de la suivante via un circuit combinatoire.
Le mot d'entrée binaire B 0 , B 1 , B 2 , B 3 est appliqué à travers le même circuit combinatoire.
Il existe deux modes dans lesquels ce circuit peut fonctionner, à savoir - le mode de décalage ou le mode de charge.
Mode de chargement
Lorsque la ligne de barre de décalage / charge est au niveau bas (0), les portes ET 2, 4 et 6 deviennent actives, elles passeront les bits B 1 , B 2 , B 3 aux bascules correspondantes. Sur le front bas de l'horloge, l'entrée binaire B 0 , B 1 , B 2 , B 3 sera chargée dans les bascules correspondantes. Ainsi, un chargement parallèle a lieu.
Mode de décalage
Lorsque la ligne de décalage / barre de charge est basse (1), les portes ET 2, 4 et 6 deviennent inactives. Par conséquent, le chargement parallèle des données devient impossible. Mais les portes ET 1, 3 et 5 deviennent actives. Par conséquent, le décalage des données de gauche à droite bit par bit lors de l'application d'impulsions d'horloge. Ainsi, l'opération parallèle en sortie série a lieu.
Diagramme
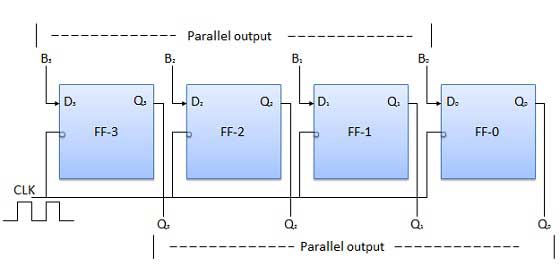
Entrée parallèle Sortie parallèle (PIPO)
Dans ce mode, l'entrée binaire B 0 , B 1 , B 2 , B 3 à 4 bits est appliquée aux entrées de données D 0 , D 1 , D 2 , D 3 respectivement des quatre bascules. Dès qu'un front d'horloge négatif est appliqué, les bits binaires d'entrée seront chargés simultanément dans les bascules. Les bits chargés apparaîtront simultanément du côté sortie. Seule l'impulsion d'horloge est indispensable pour charger tous les bits.
Diagramme
Registre à décalage bidirectionnel
Si un nombre binaire est décalé vers la gauche d'une position, cela équivaut à multiplier le nombre d'origine par 2. De même, si un nombre binaire est décalé vers la droite d'une position, cela équivaut à diviser le nombre d'origine par 2.
Par conséquent, si nous voulons utiliser le registre à décalage pour multiplier et diviser le nombre binaire donné, nous devrions être en mesure de déplacer les données dans la direction gauche ou droite.
Un tel registre est appelé registre bidirectionnel. Un registre à décalage bidirectionnel à quatre bits est représenté sur la fig.
Il y a deux entrées série, à savoir l'entrée de données de décalage de droite série DR, et l'entrée de données de décalage de gauche série DL avec une entrée de sélection de mode (M).
Diagramme
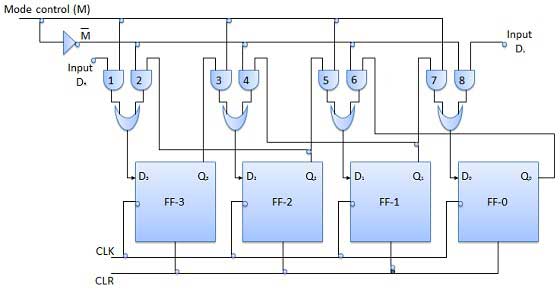
Opération
| SN | État | Opération |
|---|---|---|
| 1 | With M = 1 − Shift right operation | Si M = 1, alors les portes ET 1, 3, 5 et 7 sont activées tandis que les portes ET restantes 2, 4, 6 et 8 seront désactivées. Les données en D R sont décalées vers la droite bit par bit de FF-3 à FF-0 lors de l'application d'impulsions d'horloge. Ainsi, avec M = 1, nous obtenons l'opération de décalage à droite série. |
| 2 | With M = 0 − Shift left operation | Lorsque la commande de mode M est connectée à 0, les portes ET 2, 4, 6 et 8 sont activées tandis que 1, 3, 5 et 7 sont désactivées. Les données en D L sont décalées à gauche bit par bit de FF-0 à FF-3 lors de l'application d'impulsions d'horloge. Ainsi, avec M = 0, nous obtenons l'opération de décalage à droite série. |
Registre universel des vitesses
Un registre à décalage qui peut décaler les données dans une seule direction est appelé un registre à décalage unidirectionnel. Un registre à décalage qui peut décaler les données dans les deux sens est appelé un registre à décalage bidirectionnel. En appliquant la même logique, un registre à décalage qui peut décaler les données dans les deux sens et les charger parallèlement, est connu sous le nom de registre à décalage universel. Le registre à décalage est capable d'effectuer l'opération suivante -
- Chargement parallèle
- Décalage à gauche
- Décalage à droite
L'entrée de commande de mode est connectée à la logique 1 pour l'opération de chargement parallèle alors qu'elle est connectée à 0 pour le décalage série. Avec la broche de commande de mode connectée à la masse, le registre à décalage universel agit comme un registre bidirectionnel. Pour un fonctionnement série gauche, l'entrée est appliquée à l'entrée série qui va à la porte ET-1 représentée sur la figure. Alors que pour l'opération de décalage à droite, l'entrée série est appliquée à l'entrée D.
Diagramme
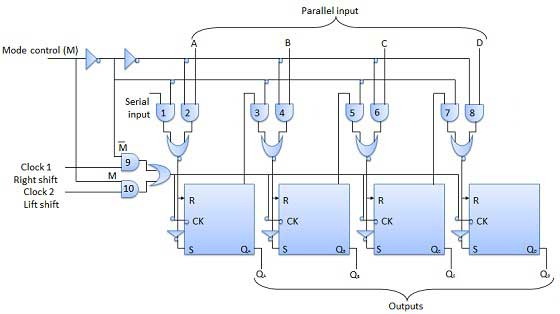
Le compteur est un circuit séquentiel. Un circuit numérique qui est utilisé pour un comptage d'impulsions est un compteur connu. Counter est l'application la plus large des bascules. C'est un groupe de bascules avec un signal d'horloge appliqué. Les compteurs sont de deux types.
- Compteurs asynchrones ou ondulés.
- Compteurs synchrones.
Compteurs asynchrones ou ondulés
Le schéma logique d'un compteur d'ondulation à 2 bits est illustré sur la figure. La bascule à bascule (T) est utilisée. Mais nous pouvons également utiliser la bascule JK avec J et K connectés en permanence à la logique 1. L'horloge externe est appliquée à l'entrée d'horloge de la bascule A et la sortie Q A est appliquée à l'entrée d'horloge de la bascule suivante. FF-B.
Diagramme logique
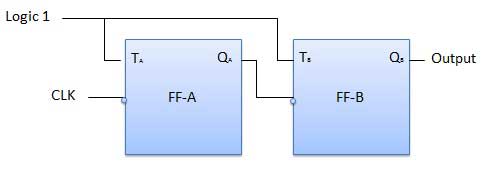
Opération
| SN | État | Opération |
|---|---|---|
| 1 | Initially let both the FFs be in the reset state | Q B Q A = 00 initialement |
| 2 | After 1st negative clock edge | Dès que le premier front d'horloge négatif est appliqué, FF-A basculera et Q A sera égal à 1. Q A est connecté à l'entrée d'horloge de FF-B. Puisque Q A est passé de 0 à 1, il est traité comme le front d'horloge positif par FF-B. Il n'y a pas de changement dans Q B car FF-B est un front négatif déclenché FF. Q B Q A = 01 après la première impulsion d'horloge. |
| 3 | After 2nd negative clock edge | A l'arrivée du deuxième front d'horloge négatif, FF-A bascule à nouveau et Q A = 0. Le changement de Q A agit comme un front d'horloge négatif pour FF-B. Donc, il basculera également, et Q B sera 1. Q B Q A = 10 après la deuxième impulsion d'horloge. |
| 4 | After 3rd negative clock edge | A l'arrivée du 3ème front d'horloge négatif, FF-A bascule à nouveau et Q A devient 1 à partir de 0. Puisqu'il s'agit d'un changement positif, FF-B n'y répond pas et reste inactif. Donc Q B ne change pas et continue d'être égal à 1. Q B Q A = 11 après la troisième impulsion d'horloge. |
| 5 | After 4th negative clock edge | A l'arrivée du 4ème front d'horloge négatif, FF-A bascule à nouveau et Q A devient 1 à partir de 0. Ce changement négatif de Q A agit comme une impulsion d'horloge pour FF-B. Par conséquent, il bascule pour changer Q B de 1 à 0. Q B Q A = 00 après la quatrième impulsion d'horloge. |
Table de vérité
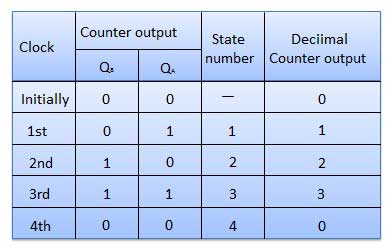
Compteurs synchrones
Si les impulsions "d'horloge" sont appliquées simultanément à toutes les bascules d'un compteur, alors un tel compteur est appelé compteur synchrone.
Compteur progressif synchrone 2 bits
Les entrées J A et K A de FF-A sont liées à la logique 1. Ainsi, FF-A fonctionnera comme une bascule à bascule. Les J B et K B entrées sont connectées à Q A .
Diagramme logique

Opération
| SN | État | Opération |
|---|---|---|
| 1 | Initially let both the FFs be in the reset state | Q B Q A = 00 initialement. |
| 2 | After 1st negative clock edge | Dès que le premier front d'horloge négatif est appliqué, FF-A bascule et Q A passe de 0 à 1. Mais au moment de l'application du front d'horloge négatif, Q A , J B = K B = 0. Donc FF-B ne changera pas son état. Donc Q B restera 0. Q B Q A = 01 après la première impulsion d'horloge. |
| 3 | After 2nd negative clock edge | A l'arrivée du deuxième front d'horloge négatif, FF-A bascule à nouveau et Q A passe de 1 à 0. Mais à cet instant, Q A était 1. Donc J B = K B = 1 et FF-B basculera. Par conséquent, Q B passe de 0 à 1. Q B Q A = 10 après la deuxième impulsion d'horloge. |
| 4 | After 3rd negative clock edge | Lors de l'application du troisième front d'horloge descendant, FF-A basculera de 0 à 1 mais il n'y a pas de changement d'état pour FF-B. Q B Q A = 11 après la troisième impulsion d'horloge. |
| 5 | After 4th negative clock edge | Lors de l'application de la prochaine impulsion d'horloge, Q A passera de 1 à 0 car Q B passera également de 1 à 0. Q B Q A = 00 après la quatrième impulsion d'horloge. |
Classification des compteurs
Selon la façon dont le comptage progresse, les compteurs synchrones ou asynchrones sont classés comme suit -
- Compteurs
- Compteurs à rebours
- Compteurs haut / bas
Compteur HAUT / BAS
Le compteur et le compteur décroissant sont combinés pour obtenir un compteur UP / DOWN. Une entrée de commande de mode (M) est également fournie pour sélectionner le mode haut ou bas. Un circuit combinatoire doit être conçu et utilisé entre chaque paire de bascules afin de réaliser l'opération de montée / descente.
- Type de compteurs haut / bas
- Compteurs d'ondulation HAUT / BAS
- Compteur synchrone HAUT / BAS
Compteurs d'ondulation HAUT / BAS
Dans le compteur d'ondulation HAUT / BAS, tous les FF fonctionnent en mode bascule. Il faut donc utiliser des bascules T ou des bascules JK. La bascule LSB reçoit directement l'horloge. Mais l'horloge pour chaque autre FF est obtenue à partir de la sortie (Q = Q bar) du FF précédent.
UP counting mode (M=0)- La sortie Q du FF précédent est connectée à l'horloge de l'étage suivant si le comptage doit être réalisé. Pour ce mode, l'entrée de sélection de mode M est à 0 logique (M = 0).
DOWN counting mode (M=1)- Si M = 1, alors la sortie Q bar du FF précédent est connectée au FF suivant. Cela fera fonctionner le compteur en mode de comptage.
Exemple
Compteur d'ondulation binaire haut / bas 3 bits.
3 bits - donc trois FF sont nécessaires.
UP / DOWN - Une entrée de contrôle de mode est donc essentielle.
Pour un compteur à ondulation ascendante, la sortie Q du FF précédent est connectée à l'entrée d'horloge du suivant.
Pour un compteur à ondulation ascendante, la sortie Q du FF précédent est connectée à l'entrée d'horloge du suivant.
Pour un compteur décroissant d'ondulation, la sortie Q bar du FF précédent est connectée à l'entrée d'horloge du suivant.
Soit la sélection de la sortie de barre Q et Q du FF précédent contrôlé par l'entrée de commande de mode M de telle sorte que, si M = 0, comptage UP. Alors connectez Q à CLK. Si M = 1, comptage DOWN. Alors connectez la barre Q à CLK.
Diagramme
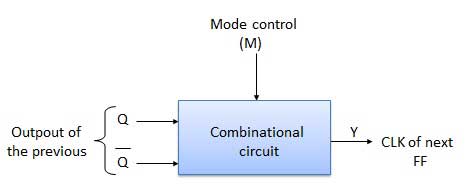
Table de vérité
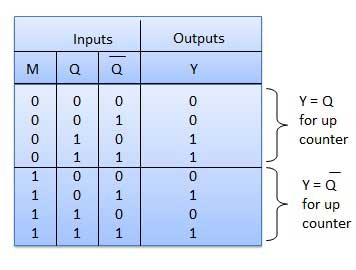
Opération
| SN | État | Opération |
|---|---|---|
| 1 | Case 1 − With M = 0 (Up counting mode) | Si M = 0 et M bar = 1, alors les portes ET 1 et 3 de la fig. sera activé tandis que les portes ET 2 et 4 seront désactivées. Par conséquent, Q A est connecté à l'entrée d'horloge de FF-B et Q B est connecté à l'entrée d'horloge de FF-C. Ces connexions sont les mêmes que celles du compteur normal. Ainsi, avec M = 0, le circuit fonctionne comme un compteur ascendant. |
| 2 | Case 2: With M = 1 (Down counting mode) | Si M = 1, alors les portes ET 2 et 4 de la fig. sont activés alors que les portes ET 1 et 3 sont désactivées. Par conséquent, la barre Q A est connectée à l'entrée d'horloge de FF-B et la barre Q B est connectée à l'entrée d'horloge de FF-C. Ces connexions produiront un décompte. Ainsi, avec M = 1, le circuit fonctionne comme un décompteur. |
Compteur de module (compteur MOD-N)
Le compteur d'ondulation 2 bits est appelé compteur MOD-4 et le compteur d'ondulation 3 bits est appelé compteur MOD-8. Ainsi, en général, un compteur d'ondulation à n bits est appelé compteur modulo-N. Où, numéro MOD = 2 n .
Type de module
- 2 bits vers le haut ou vers le bas (MOD-4)
- 3 bits vers le haut ou vers le bas (MOD-8)
- 4 bits vers le haut ou vers le bas (MOD-16)
Application des compteurs
- Compteurs de fréquence
- Horloge digitale
- Mesure du temps
- Convertisseur A vers N
- Circuits diviseurs de fréquence
- Générateur d'ondes triangulaires numériques.
Un souvenir est comme un cerveau humain. Il est utilisé pour stocker des données et des instructions. La mémoire de l'ordinateur est l'espace de stockage dans l'ordinateur où les données doivent être traitées et les instructions nécessaires au traitement sont stockées.
La mémoire est divisée en un grand nombre de petites parties. Chaque partie est appelée une cellule. Chaque emplacement ou cellule a une adresse unique qui varie de zéro à la taille de la mémoire moins un.
Par exemple, si l'ordinateur a 64 000 mots, alors cette unité de mémoire a 64 * 1024 = 65536 emplacements de mémoire. L'adresse de ces emplacements varie de 0 à 65535.
La mémoire est principalement de deux types
Internal Memory - mémoire cache et mémoire principale / principale
External Memory - disque magnétique / disque optique, etc.
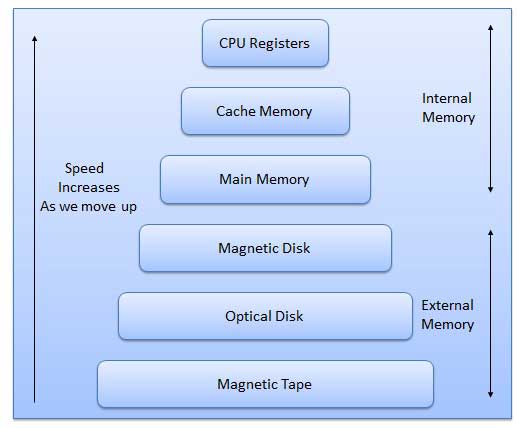
Les caractéristiques de la hiérarchie de la mémoire suivent lorsque nous allons de haut en bas.
- La capacité en termes de stockage augmente.
- Le coût par bit de stockage diminue.
- La fréquence d'accès à la mémoire par le CPU diminue.
- Le temps d'accès par le CPU augmente.
RAM
Une RAM constitue la mémoire interne de la CPU pour stocker les données, le programme et le résultat du programme. C'est une mémoire de lecture / écriture. C'est ce qu'on appelle la mémoire vive (RAM).
Étant donné que le temps d'accès dans la RAM est indépendant de l'adresse du mot, chaque emplacement de stockage à l'intérieur de la mémoire est aussi facile à atteindre qu'un autre emplacement et prend le même temps. Nous pouvons accéder à la mémoire de manière aléatoire et extrêmement rapide, mais cela peut également être assez coûteux.
La RAM est volatile, c'est-à-dire que les données qui y sont stockées sont perdues lorsque nous éteignons l'ordinateur ou en cas de panne de courant. Par conséquent, un système d'alimentation sans coupure (UPS) de secours est souvent utilisé avec les ordinateurs. La RAM est petite, à la fois en termes de taille physique et de quantité de données qu'elle peut contenir.
La RAM est de deux types
- RAM statique (SRAM)
- RAM dynamique (DRAM)
RAM statique (SRAM)
Le mot staticindique que la mémoire conserve son contenu tant que l'alimentation reste appliquée. Cependant, les données sont perdues lorsque l'alimentation est coupée en raison de la nature volatile. Les puces SRAM utilisent une matrice de 6 transistors et aucun condensateur. Les transistors ne nécessitent pas d'alimentation pour éviter les fuites, la SRAM n'a donc pas besoin d'être rafraîchie régulièrement.
En raison de l'espace supplémentaire dans la matrice, la SRAM utilise plus de puces que la DRAM pour la même quantité d'espace de stockage, augmentant ainsi les coûts de fabrication.
La RAM statique est utilisée car la mémoire cache doit être très rapide et petite.
RAM dynamique (DRAM)
DRAM, contrairement à SRAM, doit être continuellement refreshedafin qu'il conserve les données. Cela se fait en plaçant la mémoire sur un circuit de rafraîchissement qui réécrit les données plusieurs centaines de fois par seconde. La DRAM est utilisée pour la plupart de la mémoire système car elle est peu coûteuse et petite. Toutes les DRAM sont constituées de cellules mémoire. Ces cellules sont composées d'un condensateur et d'un transistor.
ROM
ROM signifie Read Only Memory. La mémoire à partir de laquelle nous ne pouvons que lire mais pas écrire dessus. Ce type de mémoire est non volatile. Les informations sont stockées en permanence dans ces mémoires lors de la fabrication.
A ROM, stores such instruction as are required to start computer when electricity is first turned on, this operation is referred to as bootstrap. ROM chip are not only used in the computer but also in other electronic items like washing machine and microwave oven.
Following are the various types of ROM −
MROM (Masked ROM)
The very first ROMs were hard-wired devices that contained a pre-programmed set of data or instructions. These kind of ROMs are known as masked ROMs. It is inexpensive ROM.
PROM (Programmable Read Only Memory)
PROM is read-only memory that can be modified only once by a user. The user buys a blank PROM and enters the desired contents using a PROM programmer. Inside the PROM chip there are small fuses which are burnt open during programming. It can be programmed only once and is not erasable.
EPROM (Erasable and Programmable Read Only Memory)
The EPROM can be erased by exposing it to ultra-violet light for a duration of upto 40 minutes. Usually, an EPROM eraser achieves this function. During programming an electrical charge is trapped in an insulated gate region. The charge is retained for more than ten years because the charge has no leakage path. For erasing this charge, ultra-violet light is passed through a quartz crystal window (lid). This exposure to ultra-violet light dissipates the charge. During normal use the quartz lid is sealed with a sticker.
EEPROM (Electrically Erasable and Programmable Read Only Memory)
The EEPROM is programmed and erased electrically. It can be erased and reprogrammed about ten thousand times. Both erasing and programming take about 4 to 10 ms (millisecond). In EEPROM, any location can be selectively erased and programmed. EEPROMs can be erased one byte at a time, rather than erasing the entire chip. Hence, the process of re-programming is flexible but slow.
Serial Access Memory
Sequential access means the system must search the storage device from the beginning of the memory address until it finds the required piece of data. Memory device which supports such access is called a Sequential Access Memory or Serial Access Memory. Magnetic tape is an example of serial access memory.
Direct Access Memory
Direct access memory or Random Access Memory, refers to conditions in which a system can go directly to the information that the user wants. Memory device which supports such access is called a Direct Access Memory. Magnetic disks, optical disks are examples of direct access memory.
Cache Memory
Cache memory is a very high speed semiconductor memory which can speed up CPU. It acts as a buffer between the CPU and main memory. It is used to hold those parts of data and program which are most frequently used by CPU. The parts of data and programs, are transferred from disk to cache memory by operating system, from where CPU can access them.
Advantages
- Cache memory is faster than main memory.
- It consumes less access time as compared to main memory.
- It stores the program that can be executed within a short period of time.
- It stores data for temporary use.
Disadvantages
- Cache memory has limited capacity.
- It is very expensive.
Virtual memory is a technique that allows the execution of processes which are not completely available in memory. The main visible advantage of this scheme is that programs can be larger than physical memory. Virtual memory is the separation of user logical memory from physical memory.
This separation allows an extremely large virtual memory to be provided for programmers when only a smaller physical memory is available. Following are the situations, when entire program is not required to be loaded fully in main memory.
User written error handling routines are used only when an error occurred in the data or computation.
Certain options and features of a program may be used rarely.
Many tables are assigned a fixed amount of address space even though only a small amount of the table is actually used.
The ability to execute a program that is only partially in memory would counter many benefits.
Less number of I/O would be needed to load or swap each user program into memory.
A program would no longer be constrained by the amount of physical memory that is available.
Each user program could take less physical memory, more programs could be run the same time, with a corresponding increase in CPU utilization and throughput.
Auxiliary Memory
Auxiliary memory is much larger in size than main memory but is slower. It normally stores system programs, instruction and data files. It is also known as secondary memory. It can also be used as an overflow/virtual memory in case the main memory capacity has been exceeded. Secondary memories cannot be accessed directly by a processor. First the data/information of auxiliary memory is transferred to the main memory and then that information can be accessed by the CPU. Characteristics of Auxiliary Memory are following −
Non-volatile memory − Data is not lost when power is cut off.
Reusable − The data stays in the secondary storage on permanent basis until it is not overwritten or deleted by the user.
Reliable − Data in secondary storage is safe because of high physical stability of secondary storage device.
Convenience − With the help of a computer software, authorised people can locate and access the data quickly.
Capacity − Secondary storage can store large volumes of data in sets of multiple disks.
Cost − It is much lesser expensive to store data on a tape or disk than primary memory.
Microprocessing unit is synonymous to central processing unit, CPU used in traditional computer. Microprocessor (MPU) acts as a device or a group of devices which do the following tasks.
- communicate with peripherals devices
- provide timing signal
- direct data flow
- perform computer tasks as specified by the instructions in memory
8085 Microprocessor
The 8085 microprocessor is an 8-bit general purpose microprocessor which is capable to address 64k of memory. This processor has forty pins, requires +5 V single power supply and a 3-MHz single-phase clock.
Block Diagram
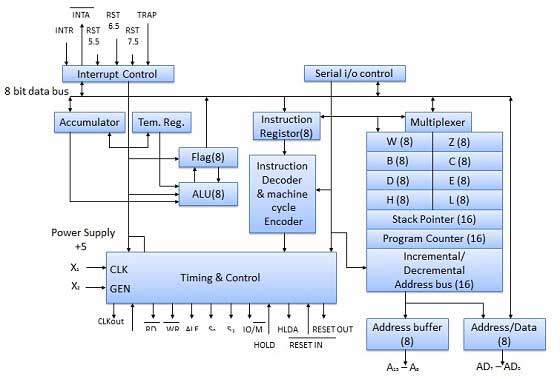
ALU
The ALU perform the computing function of microprocessor. It includes the accumulator, temporary register, arithmetic & logic circuit & and five flags. Result is stored in accumulator & flags.
Block Diagram

Accumulator
It is an 8-bit register that is part of ALU. This register is used to store 8-bit data & in performing arithmetic & logic operation. The result of operation is stored in accumulator.
Diagram
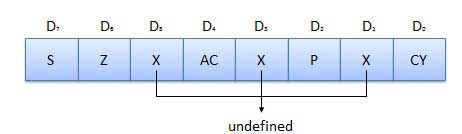
Flags
Flags are programmable. They can be used to store and transfer the data from the registers by using instruction. The ALU includes five flip-flops that are set and reset according to data condition in accumulator and other registers.
S (Sign) flag − After the execution of an arithmetic operation, if bit D7 of the result is 1, the sign flag is set. It is used to signed number. In a given byte, if D7 is 1 means negative number. If it is zero means it is a positive number.
Z (Zero) flag − The zero flag is set if ALU operation result is 0.
AC (Auxiliary Carry) flag − In arithmetic operation, when carry is generated by digit D3 and passed on to digit D4, the AC flag is set. This flag is used only internally BCD operation.
P (Parity) flag − After arithmetic or logic operation, if result has even number of 1s, the flag is set. If it has odd number of 1s, flag is reset.
C (Carry) flag − If arithmetic operation result is in a carry, the carry flag is set, otherwise it is reset.
Register section
It is basically a storage device and transfers data from registers by using instructions.
Stack Pointer (SP) − The stack pointer is also a 16-bit register which is used as a memory pointer. It points to a memory location in Read/Write memory known as stack. In between execution of program, sometime data to be stored in stack. The beginning of the stack is defined by loading a 16-bit address in the stack pointer.
Program Counter (PC) − This 16-bit register deals with fourth operation to sequence the execution of instruction. This register is also a memory pointer. Memory location have 16-bit address. It is used to store the execution address. The function of the program counter is to point to memory address from which next byte is to be fetched.
Storage registers − These registers store 8-bit data during a program execution. These registers are identified as B, C, D, E, H, L. They can be combined as register pair BC, DE and HL to perform some 16 bit operations.
Time and Control Section
This unit is responsible to synchronize Microprocessor operation as per the clock pulse and to generate the control signals which are necessary for smooth communication between Microprocessor and peripherals devices. The RD bar and WR bar signals are synchronous pulses which indicates whether data is available on the data bus or not. The control unit is responsible to control the flow of data between microprocessor, memory and peripheral devices.
PIN diagram

All the signal can be classified into six groups
| S.N. | Group | Description |
|---|---|---|
| 1 | Address bus | The 8085 microprocessor has 8 signal line, A15 - A8 which are uni directional and used as a high order address bus. |
| 2 | Data bus | The signal line AD7 - AD0 are bi-directional for dual purpose. They are used as low order address bus as well as data bus. |
| 3 | Control signal and Status signal | Control Signal RD bar − It is a read control signal (active low). If it is active then memory read the data. WR bar − It is write control signal (active low). It is active when written into selected memory. Status signal ALU (Address Latch Enable) − When ALU is high. 8085 microprocessor use address bus. When ALU is low. 8085 microprocessor is use data bus. IO/M bar − This is a status signal used to differentiate between i/o and memory operations. When it is high, it indicate an i/o operation and when it is low, it indicate memory operation. S1 and S0 − These status signals, similar to i/o and memory bar, can identify various operations, but they are rarely used in small system. |
| 4 | Power supply and frequency signal | Vcc − +5v power supply. Vss − ground reference. X, X − A crystal is connected at these two pins. The frequency is internally divided by two operate system at 3-MHz, the crystal should have a frequency of 6-MHz. CLK out − This signal can be used as the system clock for other devices. |
| 5 | Externally initiated signal | INTR (i/p) − Interrupt request. INTA bar (o/p) − It is used as acknowledge interrupt. TRAP (i/p) − This is non maskable interrupt and has highest priority. HOLD (i/p) − It is used to hold the executing program. HLDA (o/p) − Hold acknowledge. READY (i/p) − This signal is used to delay the microprocessor read or write cycle until a slow responding peripheral is ready to accept or send data. RESET IN bar − When the signal on this pin goes low, the program counter is set to zero, the bus are tri-stated, & MPU is reset. RESET OUT − This signal indicate that MPU is being reset. The signal can be used to reset other devices. RST 7.5, RST 6.5, RST 5.5 (Request interrupt) − It is used to transfer the program control to specific memory location. They have higher priority than INTR interrupt. |
| 6 | Serial I/O ports | The 8085 microprocessor has two signals to implement the serial transmission serial input data and serial output data. |
Instruction Format
Each instruction is represented by a sequence of bits within the computer. The instruction is divided into group of bits called field. The way instruction is expressed is known as instruction format. It is usually represented in the form of rectangular box. The instruction format may be of the following types.
Variable Instruction Formats
These are the instruction formats in which the instruction length varies on the basis of opcode & address specifiers. For Example, VAX instruction vary between 1 and 53 bytes while X86 instruction vary between 1 and 17 bytes.
Format

Advantage
These formats have good code density.
Drawback
These instruction formats are very difficult to decode and pipeline.
Fixed Instruction Formats
In this type of instruction format, all instructions are of same size. For Example, MIPS, Power PC, Alpha, ARM.
Format

Advantage
They are easy to decode & pipeline.
Drawback
They don't have good code density.
Hybrid Instruction Formats
In this type of instruction formats, we have multiple format length specified by opcode. For example, IBM 360/70, MIPS 16, Thumb.
Format

Advantage
These compromise between code density & instruction of these type are very easy to decode.
Addressing Modes
Addressing mode provides different ways for accessing an address to given data to a processor. Operated data is stored in the memory location, each instruction required certain data on which it has to operate. There are various techniques to specify address of data. These techniques are called Addressing Modes.
Direct addressing mode − In the direct addressing mode, address of the operand is given in the instruction and data is available in the memory location which is provided in instruction. We will move this data in desired location.
Indirect addressing mode − In the indirect addressing mode, the instruction specifies a register which contain the address of the operand. Both internal RAM and external RAM can be accessed via indirect addressing mode.
Immediate addressing mode − In the immediate addressing mode, direct data is given in the operand which move the data in accumulator. It is very fast.
Relative addressing mode − In the relative address mode, the effective address is determined by the index mode by using the program counter in stead of general purpose processor register. This mode is called relative address mode.
Index addressing mode − In the index address mode, the effective address of the operand is generated by adding a content value to the contents of the register. This mode is called index address mode.