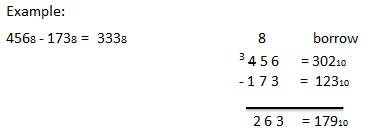Arithmétique octale
Système de nombre octal
Voici les caractéristiques d'un système de nombres octaux.
Utilise huit chiffres, 0,1,2,3,4,5,6,7.
Aussi appelé système numérique de base 8.
Chaque position dans un nombre octal représente une puissance 0 de la base (8). Exemple: 8 0
La dernière position dans un nombre octal représente une puissance x de la base (8). Exemple: 8 x où x représente la dernière position - 1.
Exemple
Numéro octal - 12570 8
Calcul de l'équivalent décimal -
| Étape | Numéro octal | Nombre décimal |
|---|---|---|
| Étape 1 | 12570 8 | ((1 × 8 4 ) + (2 × 8 3 ) + (5 × 8 2 ) + (7 × 8 1 ) + (0 × 8 0 )) 10 |
| Étape 2 | 12570 8 | (4096 + 1024 + 320 + 56 + 0) 10 |
| Étape 3 | 12570 8 | 5496 10 |
Note −12570 8 s'écrit normalement 12570.
Addition octale
Le tableau suivant d'addition octale vous aidera à gérer l'addition octale.

Pour utiliser ce tableau, suivez simplement les instructions utilisées dans cet exemple: Ajoutez 6 8 et 5 8 . Localisez 6 dans la colonne A, puis recherchez le 5 dans la colonne B. Le point dans la zone «somme» où ces deux colonnes se croisent est la «somme» de deux nombres.
68 + 58 = 138.Exemple - Addition
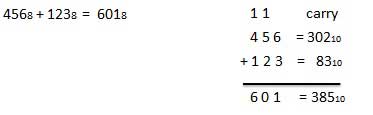
Soustraction octale
La soustraction des nombres octaux suit les mêmes règles que la soustraction des nombres dans tout autre système numérique. La seule variation est en nombre emprunté. Dans le système décimal, vous empruntez un groupe de 10 10 . Dans le système binaire, vous empruntez un groupe de 2 10 . Dans le système octal, vous empruntez un groupe de 8 10 .
Exemple - Soustraction