Cosmologie - Distance de diamètre angulaire
Dans ce chapitre, nous comprendrons ce qu'est la distance de diamètre angulaire et comment elle aide en cosmologie.
Pour l'univers actuel -
$ \ Omega_ {m, 0} \: = \: 0,3 $
$ \ Omega _ {\ wedge, 0} \: = \: 0,69 $
$ \ Omega_ {rad, 0} \: = \: 0,01 $
$ \ Omega_ {k, 0} \: = \: 0 $
Nous avons étudié deux types de distances jusqu'à présent -
Proper distance (lp) - La distance que les photons parcourent de la source à nous, c.-à-d. Instantaneous distance.
Comoving distance (lc) - Distance entre les objets dans un espace qui ne se dilate pas, c'est-à-dire distance in a comoving frame of reference.
Distance en fonction de Redshift
Considérons une galaxie qui rayonne un photon à la fois t1 qui est détecté par l'observateur à t0. Nous pouvons écrire la bonne distance à la galaxie comme -
$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$
Que le redshift de la galaxie soit z,
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$
$$ \ donc \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$
Maintenant, à tout moment la distance de la galaxie t sera -
$$ l_c = \ frac {l_p} {a (t)} $$
$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$
En termes de z,
$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$
Il existe deux façons de trouver des distances, qui sont les suivantes:
Relation flux-luminosité
$$ F = \ frac {L} {4 \ pi d ^ 2} $$
où d est la distance à la source.
La distance de diamètre angulaire d'une source
Si nous connaissons la taille d'une source, sa largeur angulaire nous indiquera sa distance par rapport à l'observateur.
$$ \ theta = \ frac {D} {l} $$
où l est la distance du diamètre angulaire de la source.
θ est la taille angulaire de la source.
D est la taille de la source.
Considérons une galaxie de taille D et de taille angulaire dθ.
Nous savons que,
$$ d \ theta = \ frac {D} {d_A} $$
$$ \ donc D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ car dr ^ 2 = 0; \: d \ phi ^ 2 \ environ 0 $$
$$ \ Flèche droite D = a (t) rd \ theta $$
En changeant r à rc, la distance comoving de la galaxie, nous avons -
$$ d \ theta = \ frac {D} {r_ca (t)} $$
Ici, si nous choisissons t = t0, nous finissons par mesurer la distance actuelle à la galaxie. MaisDest mesurée au moment de l'émission du photon. Par conséquent, en utilisantt = t0, on obtient une plus grande distance à la galaxie et donc une sous-estimation de sa taille. Par conséquent, nous devrions utiliser le tempst1.
$$ \ donc d \ theta = \ frac {D} {r_ca (t_1)} $$
En comparant cela avec le résultat précédent, nous obtenons -
$$ d_ \ wedge = a (t_1) r_c $$
$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ car 1 + z_1 = \ frac {1} {a (t_1)} $$
Par conséquent,
$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$
dA est la distance du diamètre angulaire de l'objet.
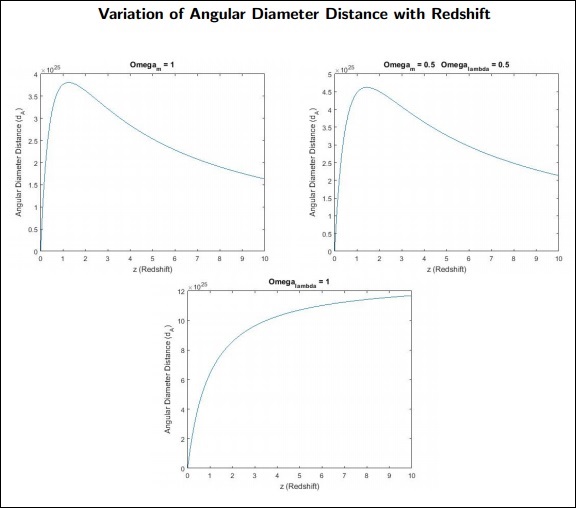
Points à retenir
Si nous connaissons la taille d'une source, sa largeur angulaire nous indiquera sa distance par rapport à l'observateur.
La distance correcte est la distance que les photons parcourent de la source à nous.
La distance comoving est la distance entre les objets dans un espace qui ne se dilate pas.