Cosmologie - Métrique Robertson-Walker
Dans ce chapitre, nous comprendrons en détail la métrique de Robertson-Walker.
Modèle pour le facteur d'échelle changeant avec le temps
Supposons qu'un photon soit émis par une galaxie lointaine. L'espace est en avant pour le photon dans toutes les directions. L'expansion de l'univers est dans toutes les directions. Voyons comment le facteur d'échelle change avec le temps dans les étapes suivantes.
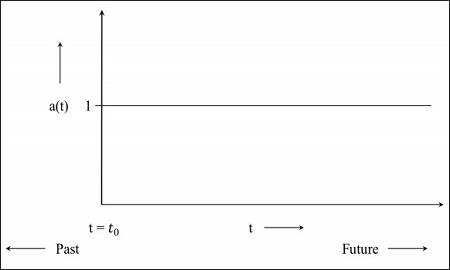
Step 1 - Pour un univers statique, le facteur d'échelle est 1, c'est-à-dire que la valeur de la distance de déplacement est la distance entre les objets.
Step 2- L'image suivante est le graphique de l'univers qui est toujours en expansion mais à un rythme décroissant, ce qui signifie que le graphique commencera dans le passé. let = 0 indique que l'univers est parti de ce point.

Step 3 - L'image suivante est le graphique de l'univers qui se développe à un rythme plus rapide.

Step 4 - L'image suivante est le graphique de l'univers qui commence à se contracter à partir de maintenant.

Si la valeur du facteur d'échelle devient 0 lors de la contraction de l'univers, cela implique que la distance entre les objets devient 0, c'est-à-dire que la distance appropriée devient 0. La distance comoving qui est la distance entre les objets dans un univers présent, est une quantité constante. À l'avenir, lorsque le facteur d'échelle devient0, tout se rapprochera. Le modèle dépend de la composante de l'univers.
La métrique pour l'univers en expansion plat (euclidien: il n'y a pas de paramètre pour la courbure) est donnée par -
$$ ds ^ 2 = a ^ 2 (t) \ left (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ right) $$
Pour l'espace-temps, l'élément de ligne que nous avons obtenu dans l'équation ci-dessus est modifié comme -
$$ ds ^ 2 = c ^ 2dt ^ 2 - \ gauche \ {a ^ 2 (t) \ gauche (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ droite) \ droite \} $$
Pour l 'espace - temps, le moment auquel le photon est émis et celui où il est détecté sont différents. La distance appropriée est la distance instantanée aux objets qui peut changer avec le temps en raison de l'expansion de l'univers. C'est la distance que le photon a parcourue depuis différents objets pour nous atteindre. Il est lié à la distance de comoving comme -
$$ d_p = a (t) \ fois d_c $$
où $ d_p $ est la distance appropriée et $ d_c $ est la distance de déplacement, qui est fixe.
La distance mesurée par rapport aux objets de l'univers actuel est considérée comme la distance de comoving, ce qui signifie que la distance de comoving est fixe et inchangée par l'expansion. Dans le passé, le facteur d'échelle était inférieur à 1, ce qui indique que la distance appropriée était plus petite.
Nous pouvons mesurer le redshift vers une galaxie. Par conséquent, la distance propre $ d_p $ correspond à $ c \ times t (z) $, où $ t (z) $ est le temps de retour vers un redshift et c est la vitesse de la lumière dans le vide. Le temps de retour est fonction du décalage vers le rouge(z).
Sur la base de la notion ci-dessus, analysons comment le décalage vers le rouge cosmologique est interprété dans ce scénario de $ d_p = a (t) \ times d_c $.
Supposons qu'un photon (qui est lié à la Terre) est émis par la galaxie, G. Le $ t_ {em} $ correspond au moment où le photon a été émis; $ a (t_ {em}) $ était le facteur d'échelle à ce moment où le photon a été émis. Au moment de la détection du photon, l'univers entier s'était étendu, c'est-à-dire que le photon est décalé vers le rouge au moment de la détection. Le $ t_ {obs} $ correspond au moment où le photon est détecté et le facteur d'échelle correspondant est $ a (t_ {obs}) $.
Le facteur par lequel l'univers a grandi est donné par -
$$ \ frac {a (t_ {obs})} {a (t_ {em})} $$
Le facteur par lequel la longueur d'onde s'est étendue est -
$$ \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
qui est égal au facteur par lequel l'univers a grandi. Les symboles ont leur signification habituelle. Par conséquent,
$$ \ frac {a (t_ {obs})} {a (t_ {em})} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} $$
Nous savons que redshift (z) est -
$$ z = \ frac {\ lambda_ {obs} - \ lambda_ {em}} {\ lambda_ {em}} = \ frac {\ lambda_ {obs}} {\ lambda_ {em}} - 1 $$
$$ 1 + z = \ frac {a (t_ {obs})} {a (t_ {em})} $$
La valeur actuelle du facteur d'échelle est 1, d'où $ a (t_ {obs}) = 1 $ et désignant le facteur d'échelle lorsque le photon a été émis dans le passé par $ a (t) $.
Par conséquent,
$$ 1 + z = \ frac {1} {a (t)} $$
Interprétation de Redshift en cosmologie
Pour comprendre cela, prenons l'exemple suivant: Si $ z = 2 $ alors $ a (t) = 1/3 $.
Cela implique que l'univers s'est agrandi d'un facteur trois depuis que la lumière a quitté cet objet. La longueur d'onde du rayonnement reçu a été multipliée par trois car l'espace s'est agrandi du même facteur lors de son transit depuis l'objet émetteur. Il convient de noter qu'à des valeurs aussi élevées dez, le redshift est principalement le redshift cosmologique, et ce n'est pas une mesure valide de la vitesse de récession réelle de l'objet par rapport à nous.
Pour le fond cosmique micro-ondes (CMB), z = 1089, ce qui signifie que l'univers actuel s'est élargi d'un facteur de ∼1090. La métrique pour l'univers plat, euclidien et en expansion est donnée par -
$$ ds ^ 2 = a ^ 2 (t) (dr ^ 2 + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2) $$
Nous souhaitons écrire la métrique dans n'importe quelle courbure.
Robertson and Walker prouvé pour tout univers de courbure (qui est homogène et isotrope), la métrique est donnée par -
$$ ds ^ 2 = a ^ 2 (t) \ left [\ frac {dr ^ 2} {1-kr ^ 2} + r ^ 2d \ theta ^ 2 + r ^ 2sin ^ 2 \ theta d \ varphi ^ 2 \ droite] $$
Ceci est généralement connu sous le nom de Robertson–Walker Metricet est vrai pour toute topologie de l'espace. Veuillez noter le facteur supplémentaire en $ dr ^ 2 $. Ici est la constante de courbure.
Géométrie de l'univers
La géométrie de l'univers est expliquée à l'aide des courbures suivantes, qui comprennent -
- Courbure positive
- Courbure négative
- Courbure zéro
Comprenons chacun de ces éléments en détail.
Courbure positive
Si un plan tangent dessiné en un point quelconque de la surface de la courbure ne se coupe en aucun point de la surface, il est appelé surface avec une courbure positive, c'est-à-dire que la surface reste d'un côté du plan tangent à ce point. La surface de la sphère a une courbure positive.
Courbure négative
Si un plan tangent dessiné en un point sur la surface de la courbure coupe en un point quelconque de la surface, il est appelé comme une surface avec une courbure négative, c'est-à-dire que la surface s'éloigne du plan tangent dans deux directions différentes. Une surface en forme de selle a une courbure négative.
Considérons maintenant la surface d'une sphère. Si un triangle est construit à la surface de la sphère en joignant trois points géodésiques (arc de grands cercles), la somme des angles intérieurs du triangle sphérique est supérieure à 180 o , soit -
$$ \ alpha + \ beta + \ gamma> \ pi $$
Ces espaces sont appelés espaces positivement courbes. De plus, la courbure est homogène et isotrope. En général, l'angle aux sommets du triangle sphérique suit la relation -
$$ \ alpha + \ beta + \ gamma = \ pi + A / R ^ 2 $$
où A est l'aire du triangle et Rest le rayon de la sphère. L'image suivante représente un espace incurvé positivement.

Pour une courbure positive, les lignes parallèles doivent se rencontrer. Considérez la surface de la terre, qui est un espace courbé positivement. Prenez deux points de départ sur l'équateur. Les lignes qui traversent l'équateur à angle droit sont appelées les lignes de longitude. Étant donné que ces lignes traversent l'équateur à angle droit, elles peuvent être appelées lignes parallèles. En partant de l'équateur, ils se croisent finalement aux pôles. Cette méthode a été utilisée parCarl Gauss et d'autres pour comprendre la topologie de la terre.
Considérons un espace incurvé négativement (une selle montrée dans l'image suivante), la somme des angles intérieurs du triangle est inférieure à 180 o , c'est-à-dire -
$$ \ alpha + \ beta + \ gamma <\ pi $$
L'angle aux sommets suit la relation -
$$ \ alpha + \ beta + \ gamma = \ pi - A / R ^ 2 $$

Courbure zéro
Une surface plane a une courbure nulle. Maintenant, pour un espace plat, si un plan est pris et un triangle est construit en joignant trois points avec géodésique (lignes droites), la somme intérieure des angles sera -
$$ \ alpha + \ beta + \ gamma = \ pi $$
L'image suivante est un espace plat à 2 dimensions.

Si l'on veut qu'un espace soit homogène et isotrope, il ne reste que trois possibilités: l'espace peut être uniformément plat ou il peut avoir une courbure positive uniforme ou il peut avoir une courbure négative uniforme.
La constante de courbure peut prendre l'une des trois valeurs suivantes.
$$ k = \ begin {cases} +1, & pour \: a \: positivement \: courbe \: space; \\\ quad 0, & pour \: a \: flat \: space; \\ - 1, & pour \: a \: négativement \: curved \: space; \ end {cases} $$
Topologie globale de l'univers
L'univers a une certaine topologie, mais localement il peut avoir des rides. En fonction de la répartition de la matière dans l'espace, les variations de courbure sont plus faibles. Supposons qu'il existe une classe d'objets qui ont la même taille réelle, peu importe où ils se trouvent dans l'univers, ce qui signifie qu'ils sont comme des bougies standard. Ils n'ont pas la même luminosité, mais ils ont la même taille.
Si l'objet est dans un espace positivement incurvé et que les photons proviennent du point A (une extrémité de l'objet) et B (l'autre extrémité de l'objet), les photons se propageront parallèlement dans l'espace positivement courbe à travers le chemin de la géodésique et ils finiront par se rencontrer . Pour un observateur en C, il semblera qu'il vienne de deux points différents dans des directions différentes.
Si l'objet est dans l'univers local et que l'on mesure la taille angulaire, il n'est pas affecté par la courbure. Si la même classe d'objets est vue à un décalage vers le rouge plus important, la taille angulaire n'est pas corrélée avec.
$$ \ theta = \ frac {d} {r} $$
Où d est la taille de l'objet et rest la distance à l'objet, c'est-à-dire que si la taille est supérieure à la taille locale, cela signifie que la courbure est positive. L'image suivante est une représentation du photon détecté dans un espace courbé positivement.

Il est à noter qu'il n'y a pas d'objet astrophysique réel qui soit de taille et de morphologie standard. Bien qu'une cD elliptique massive - les galaxies étaient censées s'adapter aux bougies standard, mais elles se sont également avérées évoluer avec le temps.
Recherche de distances par rapport aux galaxies
Dans cette section, nous allons discuter de la façon de trouver la distance à une galaxie en prenant en considération l'image suivante.

Considérons la Voie Lactée en (r, θ,) dans un cadre de repos cosmologique. On peut prendre = 0; (0, θ, ϕ), c'est à dire le centre de l'univers en invoquant l'hypothèse d'homogénéité.
Considérons une galaxie 'G' en (r1, θ,). La distance (proprement dite) est la distance radiale la plus courte parcourue par un photon. De la symétrie de l'espace-temps, la géodésique nulle de r = 0 à r = r1, a une direction constante dans l'espace. Dans sa propagation radiale, les coordonnées angulaires ne changent pas. Si les coordonnées angulaires changent, ce n'est pas le chemin le plus court. C'est la raison pour laquelle le terme de courbure est présent dans dr 2 .
Points à retenir
L'expansion de l'univers est dans toutes les directions.
L'univers peut être statique, en expansion ou en contraction selon l'évolution du facteur d'échelle.
Les galaxies cD évoluent avec le temps et ne peuvent donc pas être utilisées comme bougies standard.
L'univers a une certaine topologie, mais localement il peut avoir des rides.