Cosmologie - Univers dominé par les radiations
Dans ce chapitre, nous discuterons des solutions aux équations de Friedmann relatives à l'univers dominé par les radiations. Au début, nous comparons la densité d'énergie de la matière à celle du rayonnement. Cela nous permettra de voir si notre univers est dominé par la matière ou par les radiations.
Densité énergétique du rayonnement
Le rayonnement répandu dans l'univers actuel peut être très peu attribué aux sources stellaires, mais il est principalement dû au résidu CMB (Cosmic Microwave Background).
La densité d'énergie du rayonnement, $ \ epsilon _ {\ gamma, 0} $, peut être exprimée comme suit -
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 $$
Ici, a est la constante de rayonnement qui a l'expression $ (8 \ pi ^ 5k_B ^ 4) / (15h ^ 3c ^ 2) $ égale à a = 7.5657 × 10−15erg\: cm−3 K−4. La Température, T0, que nous considérons ici, correspond à celle du corps noir correspondant au CMB.
En substituant les résultats, nous avons,
$$ \ epsilon _ {\ gamma, 0} = aT_0 ^ 4 = 4 \ fois 10 ^ {- 13} erg \: cm ^ {- 3} $$
Densité énergétique de la matière
Dans les calculs suivants, nous avons l'hypothèse de travailler avec un univers plat et K = 0. Nous considérons la densité d'énergie de la matière comme $ \ epsilon = \ rho c ^ 2 $. Nous considérons ce qui suit -
$$ \ rho_ {m, 0} c ^ 2 = 0,3 \ rho_ {c, 0} c ^ 2 = 0,3 \ fois \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {m, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 8} erg \: cm ^ {- 3} $$
$$ \ rho_ {b, 0} c ^ 2 = 0,03 \ rho_ {c, 0} c ^ 2 = 0,03 \ times \ frac {3H_0 ^ 2} {8 \ pi G} \ times c ^ 2 $$
$$ \ rho_ {b, 0} c ^ 2 \ simeq 2 \ times 10 ^ {- 9} erg \: cm ^ {- 3} $$
Ainsi, à partir du calcul ci-dessus, nous voyons que nous vivons dans un univers dominé par la matière. Cela peut être corroboré par le fait que le CMB est très froid. En regardant en arrière dans le temps, nous aurions la température du CMB de plus en plus chaude et nous serions en mesure de conclure qu'il aurait pu y avoir une époque où l'univers était dominé par les radiations.
Variation de la densité et du facteur d'échelle
L'équation fluide nous montre que -
$$ \ dot {\ rho} + 3 \ frac {\ dot {a}} {a} \ left (\ rho + \ frac {P} {c ^ 2} \ right) = 0 $$
Si nous considérons un univers poussiéreux, nous aurions P = 0. Mis à part les résultats précédents, nous considérons l'univers comme dominé par le rayonnement.
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {P} {c ^ 2} \ right) = 0 $$
En utilisant la relation de pression de $ P_ {rad} = \ rho c ^ {2/3} $ nous avons -
$$ \ dot {\ rho} _ {rad} + 3 \ frac {\ dot {a}} {a} \ left (\ rho_ {rad} + \ frac {\ rho_ {rad}} {3} \ right) = 0 $$
$$ \ dot {\ rho} _ {rad} + 4 \ frac {\ dot {a}} {a} (\ rho_ {rad}) = 0 $$
Pour simplifier davantage, nous avons,
$$ \ frac {1} {a ^ 4} \ frac {\ mathrm {d}} {\ mathrm {d} t} (\ rho_ {rad} a ^ 4) = 0 $$
$$ \ rho_ {rad} a ^ 4 = \: constante $$
$$ \ rho_ {rad} \ propto \ frac {1} {a ^ 4} $$
Le résultat ci-dessus montre une 4 ème variation de puissance inverse de a avec $ \ rho $.
Cela peut être physiquement interprété comme $ a ^ {- 3} $ provenant de la variation de volume à mesure qu'elle augmente. Le $ a ^ {- 1} $ restant peut être traité comme l'énergie perdue par le photon en raison de l'expansion de l'espace dans l'univers (décalage vers le rouge cosmologique 1 + z = a -1 ).
L'image suivante montre la variation de la matière et de la densité de rayonnement avec le temps.
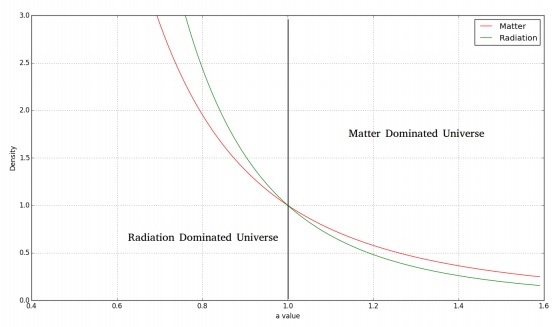
Pour un univers plat dominé par les radiations, nous aurions l'équation de Friedmann comme suit -
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G \ rho} {3} $$
$$ \ left (\ frac {\ dot {a}} {a} \ right) ^ 2 = \ frac {8 \ pi G} {3} \ frac {\ rho_0} {a ^ 4} $$
En simplifiant et en appliquant la solution à l'équation différentielle, nous avons -
$$ (\ dot {a}) ^ 2 = \ frac {8 \ pi G \ rho_0} {3a ^ 2} $$
$$ \ Rightarrow a (t) \ propto t ^ {\ frac {1} {2}} $$
Ainsi, nous avons -
$$ a (t) = a_0 \ gauche (\ frac {t} {t_0} \ droite) ^ {\ frac {1} {2}} $$
À partir de l'équation ci-dessus, nous voyons que le taux d'augmentation du facteur d'échelle est inférieur à celui de l'univers poussiéreux.
Points à retenir
Le rayonnement répandu dans l'univers actuel peut être attribué très peu aux sources stellaires.
Pour un univers poussiéreux, la pression est nulle.
CMB est très froid.