Circuits arithmétiques
Dans le chapitre précédent, nous avons discuté des applications de base de op-amp. Notez qu'ils relèvent des opérations linéaires d'un ampli-op. Dans ce chapitre, parlons des circuits arithmétiques, qui sont également des applications linéaires de l'ampli-op.
Les circuits électroniques qui effectuent des opérations arithmétiques sont appelés arithmetic circuits. En utilisant des amplificateurs opérationnels, vous pouvez construire des circuits arithmétiques de base tels qu'unadder et un subtractor. Dans ce chapitre, vous découvrirez chacun d'eux en détail.
Additionneur
Un additionneur est un circuit électronique qui produit une sortie, qui est égale à la somme des entrées appliquées. Cette section traite du circuit additionneur basé sur l'ampli opérationnel.
Un additionneur basé sur un ampli opérationnel produit une sortie égale à la somme des tensions d'entrée appliquées à sa borne inverseuse. Il est également appelé comme unsumming amplifier, puisque la sortie est amplifiée.
le circuit diagram d'un additionneur basé sur un ampli opérationnel est illustré dans la figure suivante -
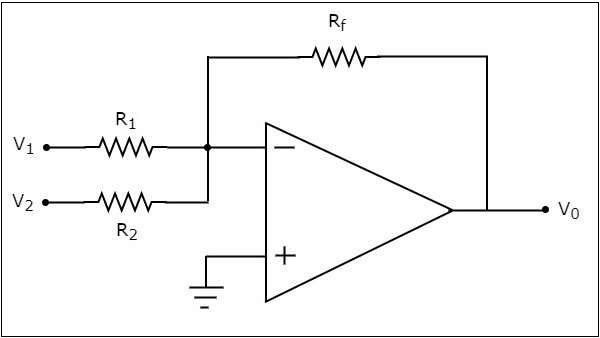
Dans le circuit ci-dessus, la borne d'entrée non inverseuse de l'amplificateur opérationnel est connectée à la terre. Cela signifie que zéro volt est appliqué à sa borne d'entrée non inverseuse.
Selon le virtual short concept, la tension à la borne d'entrée inverseuse d'un amplificateur opérationnel est la même que celle de la tension à sa borne d'entrée non inverseuse. Ainsi, la tension à la borne d'entrée inverseuse de l'ampli-op sera de zéro volt.
le nodal equation au nœud de la borne d'entrée inverseuse est
$$ \ frac {0-V_1} {R_1} + \ frac {0-V_2} {R_2} + \ frac {0-V_0} {R_f} = 0 $$
$$ => \ frac {V_1} {R_1} - \ frac {V_2} {R_2} = \ frac {V_0} {R_f} $$
$$ => V_ {0} = R_ {f} \ gauche (\ frac {V_1} {R_1} + \ frac {V_2} {R_2} \ droite) $$
Si $ R_ {f} = R_ {1} = R_ {2} = R $, alors la tension de sortie $ V_ {0} $ sera -
$$ V_ {0} = - R {} \ left (\ frac {V_1} {R} + \ frac {V_2} {R} \ right) $$
$$ => V_ {0} = - (V_ {1} + V_ {2}) $$
Par conséquent, le circuit additionneur basé sur l'ampli opérationnel décrit ci-dessus produira la somme des deux tensions d'entrée $ v_ {1} $ et $ v_ {1} $, comme sortie, lorsque toutes les résistances présentes dans le circuit sont de même valeur . Notez que la tension de sortie $ V_ {0} $ d'un circuit additionneur a unnegative sign, ce qui indique qu'il existe une différence de phase de 180 0 entre l'entrée et la sortie.
Soustracteur
Un soustracteur est un circuit électronique qui produit une sortie égale à la différence des entrées appliquées. Cette section traite du circuit de soustracteur basé sur l'ampli opérationnel.
Un soustracteur basé sur un amplificateur opérationnel produit une sortie égale à la différence des tensions d'entrée appliquées à ses bornes inverseuses et non inverseuses. Il est également appelé comme undifference amplifier, puisque la sortie est amplifiée.
le circuit diagram d'un soustracteur basé sur un ampli opérationnel est illustré dans la figure suivante -
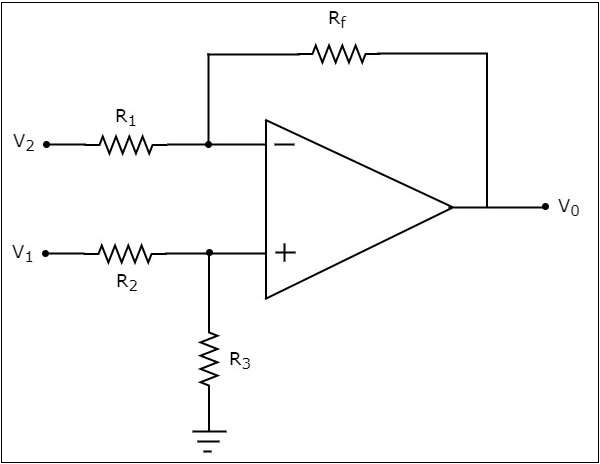
Maintenant, trouvons l'expression de la tension de sortie $ V_ {0} $ du circuit ci-dessus en utilisant superposition theorem en utilisant les étapes suivantes -
Étape 1
Tout d'abord, calculons la tension de sortie $ V_ {01} $ en ne considérant que $ V_ {1} $.
Pour cela, éliminez $ V_ {2} $ en le faisant court-circuiter. Ensuite, nous obtenons lemodified circuit diagram comme indiqué dans la figure suivante -

Maintenant, en utilisant le voltage division principle, calculez la tension à la borne d'entrée non inverseuse de l'ampli-op.
$$ => V_ {p} = V_ {1} \ gauche (\ frac {R_3} {R_2 + R_3} \ droite) $$
Maintenant, le circuit ci-dessus ressemble à un amplificateur non inverseur ayant la tension d'entrée $ V_ {p} $. Par conséquent, la tension de sortie $ V_ {01} $ du circuit ci-dessus sera
$$ V_ {01} = V_ {p} \ gauche (1+ \ frac {R_f} {R_1} \ droite) $$
En remplacement, la valeur de $ V_ {p} $ dans l'équation ci-dessus, nous obtenons la tension de sortie $ V_ {01} $ en considérant seulement $ V_ {1} $, comme -
$$ V_ {01} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) $$
Étape 2
Dans cette étape, trouvons la tension de sortie, $ V_ {02} $ en ne considérant que $ V_ {2} $. Similaire à celui de l'étape ci-dessus, éliminez $ V_ {1} $ en le faisant court-circuiter. lemodified circuit diagram est illustré dans la figure suivante.

Vous pouvez observer que la tension à la borne d'entrée non inverseuse de l'ampli-op sera de zéro volt. Cela signifie que le circuit ci-dessus est simplement uninverting op-amp. Par conséquent, la tension de sortie $ V_ {02} $ du circuit ci-dessus sera -
$$ V_ {02} = \ gauche (- \ frac {R_f} {R_1} \ droite) V_ {2} $$
Étape 3
Dans cette étape, nous obtiendrons la tension de sortie $ V_ {0} $ du circuit soustracteur par adding the output voltagesobtenu aux étapes 1 et 2. Mathématiquement, il peut être écrit comme
$$ V_ {0} = V_ {01} + V_ {02} $$
En remplaçant les valeurs de $ V_ {01} $ et $ V_ {02} $ dans l'équation ci-dessus, nous obtenons -
$$ V_ {0} = V_ {1} \ gauche (\ frac {R_3} {R_2 + R_3} \ droite) \ gauche (1+ \ frac {R_f} {R_1} \ droite) + \ gauche (- \ frac {R_f} {R_1} \ right) V_ {2} $$
$$ => V_ {0} = V_ {1} \ left (\ frac {R_3} {R_2 + R_3} \ right) \ left (1+ \ frac {R_f} {R_1} \ right) - \ left (\ frac {R_f} {R_1} \ right) V_ {2} $$
Si $ R_ {f} = R_ {1} = R_ {2} = R_ {3} = R $, alors la tension de sortie $ V_ {0} $ sera
$$ V_ {0} = V_ {1} \ gauche (\ frac {R} {R + R} \ droite) \ gauche (1+ \ frac {R} {R} \ droite) - \ gauche (\ frac { R} {R} \ droite) V_ {2} $$
$$ => V_ {0} = V_ {1} \ gauche (\ frac {R} {2R} \ droite) (2) - (1) V_ {2} $$
$$ V_ {0} = V_ {1} -V_ {2} $$
Ainsi, le circuit soustracteur basé sur l'ampli opérationnel décrit ci-dessus produira une sortie, qui est la différence de deux tensions d'entrée $ V_ {1} $ et $ V_ {2} $, lorsque toutes les résistances présentes dans le circuit sont de même valeur .