Oscillateurs sinusoïdaux
Un oscillateur est un circuit électronique qui produit un signal périodique. Si l'oscillateur produit des oscillations sinusoïdales, il est appelésinusoidal oscillator. Il convertit l'énergie d'entrée d'une source CC en une énergie de sortie CA d'un signal périodique. Ce signal périodique aura une fréquence et une amplitude spécifiques.
le block diagram d'un oscillateur sinusoïdal est illustré dans la figure suivante -
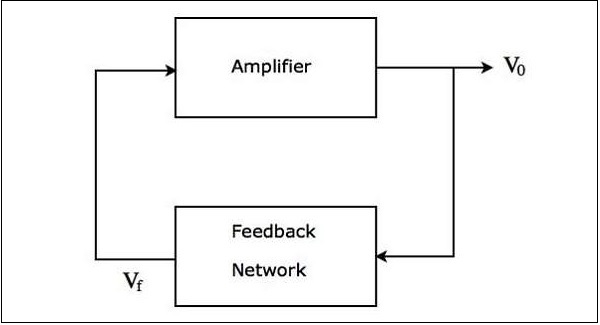
La figure ci-dessus se compose principalement de two blocks: un amplificateur et un réseau de rétroaction. Le réseau de rétroaction prend une partie de la sortie de l'amplificateur en tant qu'entrée et produit un signal de tension. Ce signal de tension est appliqué en tant qu'entrée à l'amplificateur.
Le schéma de principe d'un oscillateur sinusoïdal illustré ci-dessus produit des oscillations sinusoïdales, lorsque ce qui suit two conditions sont satisfaits -
le loop gain $ A_ {v} \ beta $ du diagramme ci-dessus de l'oscillateur sinusoïdal doit être supérieur ou égal à unity. Ici, $ A_ {v} $ et $ \ beta $ sont respectivement le gain d'amplificateur et le gain du réseau de rétroaction.
Le total phase shift autour de la boucle du schéma de principe ci-dessus d'un oscillateur sinusoïdal doit être soit 00 ou 3600.
Les deux conditions ci-dessus ensemble sont appelées comme Barkhausen criteria.
Oscillateurs basés sur un ampli opérationnel
Il y a two types d'oscillateurs basés sur un ampli opérationnel.
- Oscillateur à déphasage RC
- Oscillateur à pont de Wien
Cette section traite chacun d'eux en détail.
Oscillateur à décalage de phase RC
L'oscillateur basé sur l'ampli-op, qui produit un signal de tension sinusoïdal à la sortie à l'aide d'un amplificateur inverseur et d'un réseau de rétroaction est connu sous le nom de RC phase shift oscillator. Ce réseau de rétroaction se compose de trois sections RC en cascade.
le circuit diagram d'un oscillateur à déphasage RC est illustré dans la figure suivante -
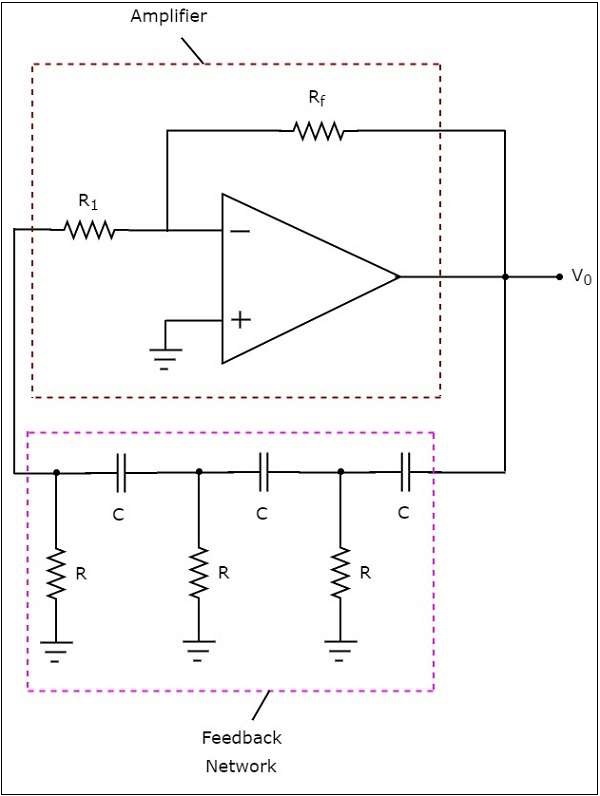
Dans le circuit ci-dessus, l'ampli-op fonctionne en inverting mode. Par conséquent, il fournit un déphasage de 180 0 . Le réseau de rétroaction présent dans le circuit ci-dessus fournit également un déphasage de 180 0 , puisque chaque section RC fournit un déphasage de 60 0 . Par conséquent, le circuit ci-dessus fournit un déphasage total de 360 ° à une certaine fréquence.
le output frequency d'un oscillateur à déphasage RC est -
$$ f = \ frac {1} {2 \ Pi RC \ sqrt [] {6}} $$
le gain $A_{v}$ d'un amplificateur inverseur doit être supérieur ou égal à -29,
$$ ie, - \ frac {R_f} {R_1} \ geq-29 $$
$$ => \ frac {R_f} {R_1} \ geq-29 $$
$$ => R_ {f} \ geq29R_ {1} $$
Donc, nous devrions considérer la valeur de la résistance de rétroaction $ R_ {f} $, comme au moins 29 fois la valeur de la résistance $ R_ {1} $, afin de produire des oscillations soutenues à la sortie d'un oscillateur à déphasage RC.
Oscillateur de pont de Wien
L'oscillateur basé sur un amplificateur opérationnel, qui produit un signal de tension sinusoïdal à la sortie à l'aide d'un amplificateur non inverseur et d'un réseau de rétroaction, est appelé Wien bridge oscillator.
le circuit diagram d'un oscillateur à pont de Wien est illustré dans la figure suivante -
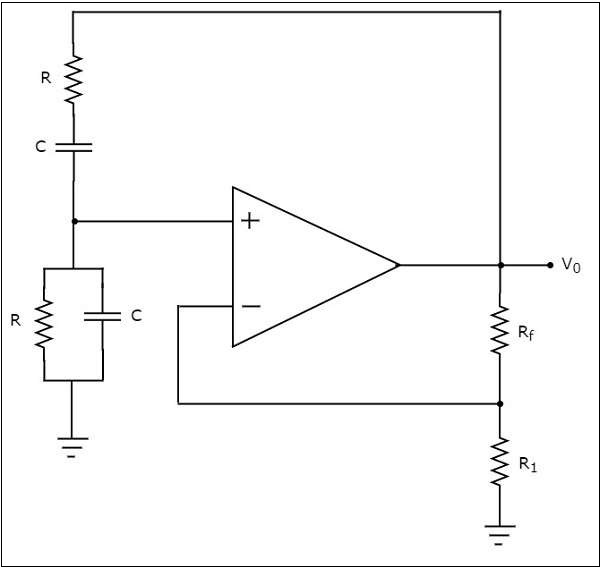
Dans le circuit illustré ci-dessus pour l'oscillateur à pont Wein, l'ampli opérationnel fonctionne en non inverting mode. Par conséquent, il fournit un déphasage de 00. Ainsi, le réseau de rétroaction présent dans le circuit ci-dessus ne doit fournir aucun déphasage.
Si le réseau de rétroaction fournit un certain déphasage, nous devons balance the bridgede manière à éviter tout déphasage. Ainsi, le circuit ci-dessus fournit un déphasage total de 0 0 à une certaine fréquence.
le output frequency de l'oscillateur à pont de Wien est
$$ f = \ frac {1} {2 \ Pi RC} $$
le gain $A_{v}$ de l'amplificateur non inverseur doit être supérieur ou égal à 3
$$ ie, 1 + \ frac {R_f} {R_1} \ geq3 $$
$$ => \ frac {R_f} {R_1} \ geq2 $$
$$ => R_ {f} \ geq2R_ {1} $$
Donc, nous devrions considérer la valeur de la résistance de rétroaction $ R_ {f} $ au moins deux fois la valeur de la résistance, $ R_ {1} $ afin de produire des oscillations soutenues à la sortie de l'oscillateur à pont de Wien.