Amplificateurs Log Et Anti Log

Les circuits électroniques qui effectuent les opérations mathématiques telles que le logarithme et l'anti-logarithme (exponentiel) avec une amplification sont appelés comme Logarithmic amplifier et Anti-Logarithmic amplifier respectivement.

Ce chapitre traite de la Logarithmic amplifier et Anti-Logarithmic amplifieren détail. Veuillez noter que ces amplificateurs relèvent d'applications non linéaires.

Amplificateur logarithmique

UNE logarithmic amplifier, ou un log amplifier, est un circuit électronique qui produit une sortie proportionnelle au logarithme de l'entrée appliquée. Cette section traite en détail de l'amplificateur logarithmique basé sur l'amplificateur opérationnel.

Un amplificateur logarithmique basé sur un amplificateur opérationnel produit une tension à la sortie, qui est proportionnelle au logarithme de la tension appliquée à la résistance connectée à sa borne inverseuse. lecircuit diagram d'un amplificateur logarithmique basé sur un amplificateur opérationnel est illustré dans la figure suivante -

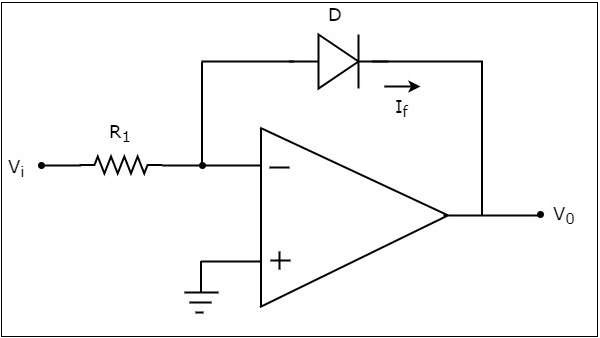
Dans le circuit ci-dessus, la borne d'entrée non inverseuse de l'amplificateur opérationnel est connectée à la terre. Cela signifie que zéro volt est appliqué à la borne d'entrée non inverseuse de l'amplificateur opérationnel.

Selon le virtual short concept, la tension à la borne d'entrée inverseuse d'un ampli opérationnel sera égale à la tension à sa borne d'entrée non inverseuse. Ainsi, la tension à la borne d'entrée inverseuse sera de zéro volt.

le nodal equation au nœud de la borne d'entrée inverseuse est -

$$ \ frac {0-V_i} {R_1} + I_ {f} = 0 $$

$$ => I_ {f} = \ frac {V_i} {R_1} ...... Équation 1 $$

Ce qui suit est le equation for current passant à travers une diode, lorsqu'elle est en polarisation directe -

$$ I_ {f} = I_ {s} e ^ {(\ frac {V_f} {nV_T})} ...... Équation 2 $$

où,

$ I_ {s} $ est le courant de saturation de la diode,

$ V_ {f} $ est la chute de tension aux bornes de la diode, lorsqu'elle est en polarisation directe,

$ V_ {T} $ est la tension thermique équivalente de la diode.

le KVL equation autour de la boucle de rétroaction de l'ampli opérationnel sera -

$$ 0-V_ {f} -V_ {0} = 0 $$

$$ => V_ {f} = - V_ {0} $$

En substituant la valeur de $ V_ {f} $ dans l'équation 2, nous obtenons -

$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} ...... Équation 3 $$

Observez que les termes du côté gauche de l'équation 1 et de l'équation 3 sont identiques. Par conséquent, assimilez le terme de droite de ces deux équations comme indiqué ci-dessous -

$$ \ frac {V_i} {R_1} = I_ {s} e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$

$$ \ frac {V_i} {R_1I_s} = e ^ {\ left (\ frac {-V_0} {nV_T} \ right)} $$

Postuler natural logarithm des deux côtés, nous obtenons -

$$ In \ left (\ frac {V_i} {R_1I_s} \ right) = \ frac {-V_0} {nV_T} $$

$$ V_ {0} = - {nV_T} In \ left (\ frac {V_i} {R_1I_s} \ right) $$

Notez que dans l'équation ci-dessus, les paramètres n, $ {V_T} $ et $ I_ {s} $ sont des constantes. Ainsi, la tension de sortie $ V_ {0} $ sera proportionnelle aunatural logarithm de la tension d'entrée $ V_ {i} $ pour une valeur fixe de résistance $ R_ {1} $.

Par conséquent, le circuit amplificateur logarithmique basé sur l'amplificateur opérationnel décrit ci-dessus produira une sortie, qui est proportionnelle au logarithme naturel de la tension d'entrée $ {V_T} $, lorsque $ {R_1I_s} = 1V $.

Observez que la tension de sortie $ V_ {0} $ a un negative sign, ce qui indique qu'il existe une différence de phase de 180 ⁰ entre l'entrée et la sortie.

Amplificateur anti-logarithmique

Un anti-logarithmic amplifier, ou un anti-log amplifier, est un circuit électronique qui produit une sortie proportionnelle à l'anti-logarithme de l'entrée appliquée. Cette section traite en détail de l'amplificateur anti-logarithmique basé sur l'amplificateur opérationnel.

Un amplificateur anti-logarithmique basé sur un amplificateur opérationnel produit une tension en sortie, qui est proportionnelle à l'anti-logarithme de la tension appliquée à la diode connectée à sa borne inverseuse.

le circuit diagram d'un amplificateur anti-logarithmique basé sur un amplificateur opérationnel est illustré dans la figure suivante -

Dans le circuit illustré ci-dessus, la borne d'entrée non inverseuse de l'amplificateur opérationnel est connectée à la masse. Cela signifie que zéro volt est appliqué à sa borne d'entrée non inverseuse.

Selon le virtual short concept, la tension à la borne d'entrée inverseuse de l'ampli-op sera égale à la tension présente sur sa borne d'entrée non inverseuse. Ainsi, la tension à sa borne d'entrée inverseuse sera de zéro volt.

le nodal equation au nœud de la borne d'entrée inverseuse est -

$$ - I_ {f} + \ frac {0-V_0} {R_f} = 0 $$

$$ => - \ frac {V_0} {R_f} = I_ {f} $$

$$ => V_ {0} = - R_ {f} I_ {f} ......... Équation 4 $$

Nous savons que l'équation du courant circulant dans une diode, lorsqu'elle est en polarisation directe, est la suivante:

$$ I_ {f} = I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)} $$

En remplaçant la valeur de $ I_ {f} $ dans l'équation 4, nous obtenons

$$ V_ {0} = - R_ {f} \ left \ {{I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} \ right \} $$

$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_f} {nV_T} \ right)}} ...... Équation 5 $$

L'équation KVL du côté entrée de la borne inverseuse de l'ampli opérationnel sera

$$ V_ {i} -V_ {f} = 0 $$

$$ V_ {f} = V_ {i} $$

En substituant, la valeur de dans l'équation 5, nous obtenons -

$$ V_ {0} = - R_ {f} {I_ {s} e ^ {\ left (\ frac {V_i} {nV_T} \ right)}} $$

Notez que, dans l'équation ci-dessus, les paramètres n, $ {V_T} $ et $ I_ {s} $ sont des constantes. Ainsi, la tension de sortie $ {V_0} $ sera proportionnelle auanti-natural logarithm (exponentielle) de la tension d'entrée $ {V_i} $, pour une valeur fixe de la résistance de rétroaction $ {R_f} $.

Par conséquent, le circuit amplificateur anti-logarithmique basé sur l'ampli-op décrit ci-dessus produira une sortie, qui est proportionnelle au logarithme anti-naturel (exponentiel) de la tension d'entrée $ {V_i} $ quand, $ {R_fI_s} = 1V $. Observez que la tension de sortie $ {V_0} $ a unnegative sign, ce qui indique qu'il existe une différence de phase de 180 ⁰ entre l'entrée et la sortie.