SciPy - Interpoler

Dans ce chapitre, nous expliquerons comment l'interpolation aide dans SciPy.

Qu'est-ce que l'interpolation?

L'interpolation est le processus de recherche d'une valeur entre deux points sur une ligne ou une courbe. Pour nous aider à nous souvenir de ce que cela signifie, nous devrions penser à la première partie du mot «inter» comme signifiant «entrer», ce qui nous rappelle de regarder «à l'intérieur» des données que nous avions à l'origine. Cet outil, l'interpolation, n'est pas seulement utile dans les statistiques, mais est également utile dans la science, les affaires ou lorsqu'il est nécessaire de prédire des valeurs comprises dans deux points de données existants.

Créons quelques données et voyons comment cette interpolation peut être effectuée en utilisant le scipy.interpolate paquet.

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
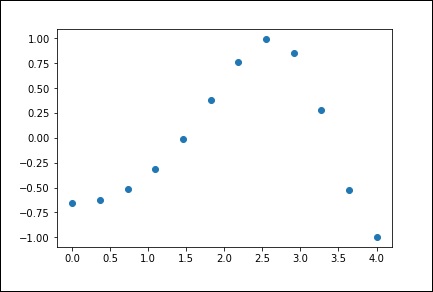
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print x,y

Le programme ci-dessus générera la sortie suivante.

(
   array([0.,  0.36363636,  0.72727273,  1.09090909,  1.45454545, 1.81818182, 
          2.18181818,  2.54545455,  2.90909091,  3.27272727,  3.63636364,  4.]),
            
   array([-0.65364362,  -0.61966189,  -0.51077021,  -0.31047698,  -0.00715476,
           0.37976236,   0.76715099,   0.99239518,   0.85886263,   0.27994201,
          -0.52586509,  -0.99582185])
)

Maintenant, nous avons deux tableaux. En supposant que ces deux tableaux sont les deux dimensions des points dans l'espace, traçons en utilisant le programme suivant et voyons à quoi ils ressemblent.

plt.plot(x, y,’o’)
plt.show()

Le programme ci-dessus générera la sortie suivante.

Interpolation 1D

La classe interp1d dans scipy.interpolate est une méthode pratique pour créer une fonction basée sur des points de données fixes, qui peut être évaluée n'importe où dans le domaine défini par les données données à l'aide d'une interpolation linéaire.

En utilisant les données ci-dessus, créons une fonction d'interpolation et dessinons un nouveau graphe interpolé.

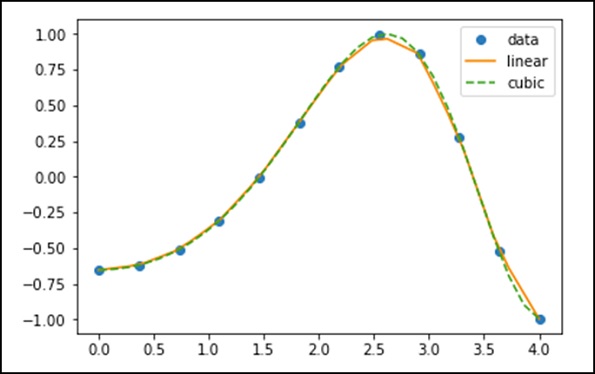
f1 = interp1d(x, y,kind = 'linear')

f2 = interp1d(x, y, kind = 'cubic')

En utilisant la fonction interp1d, nous avons créé deux fonctions f1 et f2. Ces fonctions, pour une entrée donnée, x renvoie y. Le troisième type de variable représente le type de la technique d'interpolation. «Linéaire», «Le plus proche», «Zéro», «Slinear», «Quadratic», «Cubic» sont quelques techniques d'interpolation.

Maintenant, créons une nouvelle entrée de plus de longueur pour voir la nette différence d'interpolation. Nous utiliserons la même fonction des anciennes données sur les nouvelles données.

xnew = np.linspace(0, 4,30)

plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')

plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')

plt.show()

Le programme ci-dessus générera la sortie suivante.

Cannelures

Pour dessiner des courbes lisses à travers des points de données, les dessinateurs utilisaient autrefois de fines bandes flexibles de bois, de caoutchouc dur, de métal ou de plastique appelées cannelures mécaniques. Pour utiliser une spline mécanique, des broches ont été placées à une sélection judicieuse de points le long d'une courbe dans un dessin, puis la spline a été pliée, de sorte qu'elle touche chacune de ces broches.

Clairement, avec cette construction, la spline interpole la courbe au niveau de ces broches. Il peut être utilisé pour reproduire la courbe dans d'autres dessins. Les points où se trouvent les broches s'appellent des nœuds. Nous pouvons changer la forme de la courbe définie par la spline en ajustant l'emplacement des nœuds.

Spline univariée

La spline de lissage unidimensionnelle s'adapte à un ensemble donné de points de données. La classe UnivariateSpline dans scipy.interpolate est une méthode pratique pour créer une fonction, basée sur la classe de points de données fixes - scipy.interpolate.UnivariateSpline (x, y, w = None, bbox = [None, None], k = 3, s = Aucun, ext = 0, check_finite = False).

Parameters - Voici les paramètres d'une spline univariée.

Cela ajuste une spline y = spl (x) de degré k aux données x, y fournies.
'w' - Spécifie les poids pour l'ajustement de spline. Doit être positif. Si aucun (par défaut), les poids sont tous égaux.
's' - Spécifie le nombre de nœuds en spécifiant une condition de lissage.
'k' - Degré de la spline de lissage. Doit être <= 5. La valeur par défaut est k = 3, une spline cubique.
Ext - Contrôle le mode d'extrapolation pour les éléments qui ne sont pas dans l'intervalle défini par la séquence de nœuds.

si ext = 0 ou 'extrapolate', renvoie la valeur extrapolée.
si ext = 1 ou 'zéro', renvoie 0
si ext = 2 ou 'rise', déclenche une ValueError
si ext = 3 de 'const', renvoie la valeur limite.

check_finite - Indique s'il faut vérifier que les tableaux d'entrée ne contiennent que des nombres finis.

Prenons l'exemple suivant.

import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
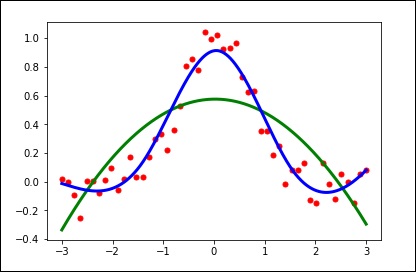
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()

Utilisez la valeur par défaut pour le paramètre de lissage.

spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()

Modifiez manuellement la quantité de lissage.

spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()