SciPy - ODR
ODR signifie Orthogonal Distance Regression, qui est utilisé dans les études de régression. La régression linéaire de base est souvent utilisée pour estimer la relation entre les deux variablesy et x en traçant la ligne de meilleur ajustement sur le graphique.
La méthode mathématique utilisée pour cela est connue sous le nom de Least Squares, et vise à minimiser la somme de l'erreur quadratique pour chaque point. La question clé ici est de savoir comment calculer l'erreur (également appelée résidu) pour chaque point?
Dans une régression linéaire standard, le but est de prédire la valeur Y à partir de la valeur X - donc la chose sensée à faire est de calculer l'erreur dans les valeurs Y (indiquées par les lignes grises dans l'image suivante). Cependant, il est parfois plus judicieux de prendre en compte l'erreur à la fois en X et en Y (comme le montrent les lignes rouges en pointillés dans l'image suivante).
Par exemple - Lorsque vous savez que vos mesures de X sont incertaines, ou lorsque vous ne voulez pas vous concentrer sur les erreurs d'une variable par rapport à une autre.
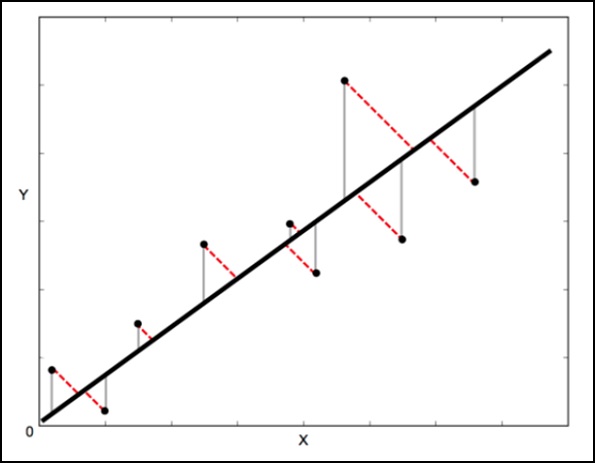
La régression de distance orthogonale (ODR) est une méthode qui peut le faire (orthogonale dans ce contexte signifie perpendiculaire - elle calcule donc les erreurs perpendiculaires à la ligne, plutôt que simplement «verticalement»).
Implémentation scipy.odr pour la régression univariée
L'exemple suivant illustre l'implémentation de scipy.odr pour la régression univariée.
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()Le programme ci-dessus générera la sortie suivante.
Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [ 0.7786442 2.33126407]
Beta Covariance: [
[ 1.93150969 -4.82877433]
[ -4.82877433 17.31417201
]]
Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
Sum of squares convergence