SciPy - Guide rapide
SciPy, prononcé comme Sigh Pi, est un open source scientifique python, distribué sous la bibliothèque sous licence BSD pour effectuer des calculs mathématiques, scientifiques et d'ingénierie.
La bibliothèque SciPy dépend de NumPy, qui permet une manipulation pratique et rapide des tableaux en N dimensions. La bibliothèque SciPy est conçue pour fonctionner avec les tableaux NumPy et fournit de nombreuses pratiques numériques conviviales et efficaces telles que des routines d'intégration et d'optimisation numériques. Ensemble, ils fonctionnent sur tous les systèmes d'exploitation courants, sont rapides à installer et sont gratuits. NumPy et SciPy sont faciles à utiliser, mais suffisamment puissants pour pouvoir compter sur certains des plus grands scientifiques et ingénieurs du monde.
Sous-packages SciPy
SciPy est organisé en sous-packages couvrant différents domaines de calcul scientifique. Ceux-ci sont résumés dans le tableau suivant -
| scipy.cluster | Quantification vectorielle / Kmeans |
| scipy.constants | Constantes physiques et mathématiques |
| scipy.fftpack | Transformée de Fourier |
| scipy.integrate | Routines d'intégration |
| scipy.interpolate | Interpolation |
| scipy.io | Entrée et sortie de données |
| scipy.linalg | Routines d'algèbre linéaire |
| scipy.ndimage | paquet d'images en n dimensions |
| scipy.odr | Régression de distance orthogonale |
| scipy.optimize | Optimisation |
| scipy.signal | Traitement de signal |
| scipy.sparse | Matrices clairsemées |
| scipy.spatial | Structures de données spatiales et algorithmes |
| scipy.special | Toutes les fonctions mathématiques spéciales |
| scipy.stats | Statistiques |
Structure de données
La structure de données de base utilisée par SciPy est un tableau multidimensionnel fourni par le module NumPy. NumPy fournit certaines fonctions pour l'algèbre linéaire, les transformées de Fourier et la génération de nombres aléatoires, mais pas avec la généralité des fonctions équivalentes dans SciPy.
La distribution Python standard n'est fournie avec aucun module SciPy. Une alternative légère consiste à installer SciPy à l'aide du programme d'installation de package Python populaire,
pip install pandasSi nous installons le Anaconda Python package, Pandas sera installé par défaut. Vous trouverez ci-dessous les packages et les liens pour les installer dans différents systèmes d'exploitation.
les fenêtres
Anaconda (de https://www.continuum.io) est une distribution Python gratuite pour la pile SciPy. Il est également disponible pour Linux et Mac.
Canopy (https://www.enthought.com/products/canopy/) est disponible gratuitement, ainsi que pour une distribution commerciale avec une pile SciPy complète pour Windows, Linux et Mac.
Python (x,y)- Il s'agit d'une distribution Python gratuite avec la pile SciPy et Spyder IDE pour Windows OS. (Téléchargeable depuishttps://python-xy.github.io/)
Linux
Les gestionnaires de packages des distributions Linux respectives sont utilisés pour installer un ou plusieurs packages dans la pile SciPy.
Ubuntu
Nous pouvons utiliser le chemin suivant pour installer Python dans Ubuntu.
sudo apt-get install python-numpy python-scipy
python-matplotlibipythonipython-notebook python-pandas python-sympy python-noseFeutre
Nous pouvons utiliser le chemin suivant pour installer Python dans Fedora.
sudo yum install numpyscipy python-matplotlibipython python-pandas
sympy python-nose atlas-develPar défaut, toutes les fonctions NumPy sont disponibles via l'espace de noms SciPy. Il n'est pas nécessaire d'importer explicitement les fonctions NumPy lorsque SciPy est importé. L'objet principal de NumPy est le tableau multidimensionnel homogène. C'est une table d'éléments (généralement des nombres), tous du même type, indexés par un tuple d'entiers positifs. Dans NumPy, les dimensions sont appelées axes. Le nombre deaxes s'appelle comme rank.
Maintenant, révisons la fonctionnalité de base des vecteurs et des matrices dans NumPy. Comme SciPy est construit sur des tableaux NumPy, la compréhension des bases de NumPy est nécessaire. Comme la plupart des parties de l'algèbre linéaire ne traitent que des matrices.
Vecteur NumPy
Un vecteur peut être créé de plusieurs manières. Certains d'entre eux sont décrits ci-dessous.
Conversion d'objets de type tableau Python en NumPy
Prenons l'exemple suivant.
import numpy as np
list = [1,2,3,4]
arr = np.array(list)
print arrLa sortie du programme ci-dessus sera la suivante.
[1 2 3 4]Création de tableau NumPy intrinsèque
NumPy a des fonctions intégrées pour créer des tableaux à partir de zéro. Certaines de ces fonctions sont expliquées ci-dessous.
Utiliser des zéros ()
La fonction zéros (forme) créera un tableau rempli de valeurs 0 avec la forme spécifiée. Le dtype par défaut est float64. Prenons l'exemple suivant.
import numpy as np
print np.zeros((2, 3))La sortie du programme ci-dessus sera la suivante.
array([[ 0., 0., 0.],
[ 0., 0., 0.]])Utiliser des uns ()
La fonction ones (forme) créera un tableau rempli de 1 valeurs. Il est identique aux zéros à tous les autres égards. Prenons l'exemple suivant.
import numpy as np
print np.ones((2, 3))La sortie du programme ci-dessus sera la suivante.
array([[ 1., 1., 1.],
[ 1., 1., 1.]])Utiliser arange ()
La fonction arange () créera des tableaux avec des valeurs incrémentées régulièrement. Prenons l'exemple suivant.
import numpy as np
print np.arange(7)Le programme ci-dessus générera la sortie suivante.
array([0, 1, 2, 3, 4, 5, 6])Définition du type de données des valeurs
Prenons l'exemple suivant.
import numpy as np
arr = np.arange(2, 10, dtype = np.float)
print arr
print "Array Data Type :",arr.dtypeLe programme ci-dessus générera la sortie suivante.
[ 2. 3. 4. 5. 6. 7. 8. 9.]
Array Data Type : float64Utilisation de linspace ()
La fonction linspace () créera des tableaux avec un nombre spécifié d'éléments, qui seront espacés de manière égale entre les valeurs de début et de fin spécifiées. Prenons l'exemple suivant.
import numpy as np
print np.linspace(1., 4., 6)Le programme ci-dessus générera la sortie suivante.
array([ 1. , 1.6, 2.2, 2.8, 3.4, 4. ])Matrice
Une matrice est un tableau 2-D spécialisé qui conserve sa nature 2-D grâce à des opérations. Il a certains opérateurs spéciaux, tels que * (multiplication de matrice) et ** (puissance de matrice). Prenons l'exemple suivant.
import numpy as np
print np.matrix('1 2; 3 4')Le programme ci-dessus générera la sortie suivante.
matrix([[1, 2],
[3, 4]])Transposition conjuguée de la matrice
Cette fonction renvoie la transposition conjuguée (complexe) de self. Prenons l'exemple suivant.
import numpy as np
mat = np.matrix('1 2; 3 4')
print mat.HLe programme ci-dessus générera la sortie suivante.
matrix([[1, 3],
[2, 4]])Transposer la matrice
Cette fonction renvoie la transposition de soi. Prenons l'exemple suivant.
import numpy as np
mat = np.matrix('1 2; 3 4')
mat.TLe programme ci-dessus générera la sortie suivante.
matrix([[1, 3],
[2, 4]])Quand on transpose une matrice, on fabrique une nouvelle matrice dont les lignes sont les colonnes de l'original. Une transposition conjuguée, par contre, intervertit la ligne et l'index de colonne pour chaque élément de la matrice. L'inverse d'une matrice est une matrice qui, si elle est multipliée par la matrice d'origine, aboutit à une matrice d'identité.
K-means clusteringest une méthode pour trouver des clusters et des centres de clusters dans un ensemble de données non étiquetées. Intuitivement, nous pourrions penser à un cluster comme - comprenant un groupe de points de données, dont les distances entre les points sont petites comparées aux distances des points à l'extérieur du cluster. Étant donné un ensemble initial de K centres, l'algorithme K-means itère les deux étapes suivantes -
Pour chaque centre, le sous-ensemble de points d'entraînement (sa grappe) qui en est le plus proche est identifié que tout autre centre.
La moyenne de chaque entité pour les points de données dans chaque cluster est calculée, et ce vecteur moyen devient le nouveau centre de ce cluster.
Ces deux étapes sont répétées jusqu'à ce que les centres ne bougent plus ou que les affectations ne changent plus. Puis, un nouveau pointxpeut être affecté au cluster du prototype le plus proche. La bibliothèque SciPy fournit une bonne implémentation de l'algorithme K-Means via le package cluster. Comprenons comment l'utiliser.
Implémentation de K-Means dans SciPy
Nous comprendrons comment implémenter K-Means dans SciPy.
Importer des K-Means
Nous verrons l'implémentation et l'utilisation de chaque fonction importée.
from SciPy.cluster.vq import kmeans,vq,whitenGénération de données
Nous devons simuler certaines données pour explorer le clustering.
from numpy import vstack,array
from numpy.random import rand
# data generation with three features
data = vstack((rand(100,3) + array([.5,.5,.5]),rand(100,3)))Maintenant, nous devons vérifier les données. Le programme ci-dessus générera la sortie suivante.
array([[ 1.48598868e+00, 8.17445796e-01, 1.00834051e+00],
[ 8.45299768e-01, 1.35450732e+00, 8.66323621e-01],
[ 1.27725864e+00, 1.00622682e+00, 8.43735610e-01],
…………….Normaliser un groupe d'observations par entité. Avant d'exécuter K-Means, il est avantageux de redimensionner chaque dimension d'entité de l'ensemble d'observation avec un blanchiment. Chaque entité est divisée par son écart type sur toutes les observations pour lui donner une variance unitaire.
Blanchir les données
Nous devons utiliser le code suivant pour blanchir les données.
# whitening of data
data = whiten(data)Calculer des K-Means avec trois clusters
Calculons maintenant des K-Means avec trois clusters en utilisant le code suivant.
# computing K-Means with K = 3 (2 clusters)
centroids,_ = kmeans(data,3)Le code ci-dessus effectue des K-Means sur un ensemble de vecteurs d'observation formant des K clusters. L'algorithme K-Means ajuste les centres de gravité jusqu'à ce que des progrès suffisants ne puissent pas être réalisés, c'est-à-dire le changement de distorsion, puisque la dernière itération est inférieure à un certain seuil. Ici, nous pouvons observer le centroïde du cluster en imprimant la variable centroïdes en utilisant le code donné ci-dessous.
print(centroids)Le code ci-dessus générera la sortie suivante.
print(centroids)[ [ 2.26034702 1.43924335 1.3697022 ]
[ 2.63788572 2.81446462 2.85163854]
[ 0.73507256 1.30801855 1.44477558] ]Attribuez chaque valeur à un cluster en utilisant le code ci-dessous.
# assign each sample to a cluster
clx,_ = vq(data,centroids)le vq fonction compare chaque vecteur d'observation dans le 'M' par 'N' obstableau avec les centres de gravité et attribue l’observation au cluster le plus proche. Il renvoie le cluster de chaque observation et la distorsion. Nous pouvons également vérifier la distorsion. Vérifions le cluster de chaque observation à l'aide du code suivant.
# check clusters of observation
print clxLe code ci-dessus générera la sortie suivante.
array([1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 2, 0, 2, 0, 1, 1, 1,
0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0,
0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 0, 0,
2, 2, 2, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2], dtype=int32)Les valeurs distinctes 0, 1, 2 du tableau ci-dessus indiquent les clusters.
Le package de constantes SciPy fournit une large gamme de constantes, qui sont utilisées dans le domaine scientifique général.
Paquet de constantes SciPy
le scipy.constants packagefournit diverses constantes. Nous devons importer la constante requise et les utiliser selon l'exigence. Voyons comment ces variables constantes sont importées et utilisées.
Pour commencer, comparons la valeur 'pi' en considérant l'exemple suivant.
#Import pi constant from both the packages
from scipy.constants import pi
from math import pi
print("sciPy - pi = %.16f"%scipy.constants.pi)
print("math - pi = %.16f"%math.pi)Le programme ci-dessus générera la sortie suivante.
sciPy - pi = 3.1415926535897931
math - pi = 3.1415926535897931Liste des constantes disponibles
Les tableaux suivants décrivent brièvement les différentes constantes.
Constantes mathématiques
| Sr. No. | Constant | La description |
|---|---|---|
| 1 | pi | pi |
| 2 | d'or | Nombre d'or |
Constantes physiques
Le tableau suivant répertorie les constantes physiques les plus couramment utilisées.
| Sr. No. | Constante et description |
|---|---|
| 1 | c Vitesse de la lumière dans le vide |
| 2 | speed_of_light Vitesse de la lumière dans le vide |
| 3 | h Constante de Planck |
| 4 | Planck Constante de Planck h |
| 5 | G Constante gravitationnelle de Newton |
| 6 | e Charge élémentaire |
| sept | R Constante de gaz molaire |
| 8 | Avogadro Constante d'Avogadro |
| 9 | k Constante de Boltzmann |
| dix | electron_mass(OR) m_e Masse électronique |
| 11 | proton_mass (OR) m_p Masse de protons |
| 12 | neutron_mass(OR)m_n Masse neutronique |
Unités
Le tableau suivant contient la liste des unités SI.
| Sr. No. | Unité | Valeur |
|---|---|---|
| 1 | milli | 0,001 |
| 2 | micro | 1e-06 |
| 3 | kilo | 1000 |
Ces unités vont de yotta, zetta, exa, peta, tera …… kilo, hector,… nano, pico,… à zepto.
Autres constantes importantes
Le tableau suivant répertorie d'autres constantes importantes utilisées dans SciPy.
| Sr. No. | Unité | Valeur |
|---|---|---|
| 1 | gramme | 0,001 kg |
| 2 | masse atomique | Constante de masse atomique |
| 3 | diplôme | Diplôme en radians |
| 4 | minute | Une minute en secondes |
| 5 | journée | Un jour en quelques secondes |
| 6 | pouce | Un pouce en mètres |
| sept | micron | Un micron en mètres |
| 8 | année-lumière | Une année-lumière en mètres |
| 9 | au m | Atmosphère standard à pascals |
| dix | acre | Un acre en mètres carrés |
| 11 | litre | Un litre en mètres cubes |
| 12 | gallon | Un gallon en mètres cubes |
| 13 | kmh | Kilomètres par heure en mètres par secondes |
| 14 | degree_Fahrenheit | Un Fahrenheit à Kelvins |
| 15 | eV | Un électron volt en joules |
| 16 | hp | Une puissance en watts |
| 17 | dyn | Un dyne en newtons |
| 18 | lambda2nu | Convertir la longueur d'onde en fréquence optique |
Se souvenir de tout cela est un peu difficile. Le moyen facile d'obtenir quelle clé correspond à quelle fonction est avec lescipy.constants.find()méthode. Prenons l'exemple suivant.
import scipy.constants
res = scipy.constants.physical_constants["alpha particle mass"]
print resLe programme ci-dessus générera la sortie suivante.
[
'alpha particle mass',
'alpha particle mass energy equivalent',
'alpha particle mass energy equivalent in MeV',
'alpha particle mass in u',
'electron to alpha particle mass ratio'
]Cette méthode renvoie la liste des clés, sinon rien si le mot clé ne correspond pas.
Fourier Transformationest calculé sur un signal du domaine temporel pour vérifier son comportement dans le domaine fréquentiel. La transformation de Fourier trouve son application dans des disciplines telles que le traitement du signal et du bruit, le traitement d'image, le traitement du signal audio, etc. SciPy propose le module fftpack, qui permet à l'utilisateur de calculer rapidement des transformées de Fourier.
Voici un exemple de fonction sinus, qui sera utilisée pour calculer la transformée de Fourier à l'aide du module fftpack.
Transformée de Fourier Rapide
Comprenons en détail ce qu'est la transformée de Fourier rapide.
Transformée de Fourier discrète unidimensionnelle
La FFT y [k] de longueur N de la séquence longueur-N x [n] est calculée par fft () et la transformée inverse est calculée en utilisant ifft (). Prenons l'exemple suivant
#Importing the fft and inverse fft functions from fftpackage
from scipy.fftpack import fft
#create an array with random n numbers
x = np.array([1.0, 2.0, 1.0, -1.0, 1.5])
#Applying the fft function
y = fft(x)
print yLe programme ci-dessus générera la sortie suivante.
[ 4.50000000+0.j 2.08155948-1.65109876j -1.83155948+1.60822041j
-1.83155948-1.60822041j 2.08155948+1.65109876j ]Regardons un autre exemple
#FFT is already in the workspace, using the same workspace to for inverse transform
yinv = ifft(y)
print yinvLe programme ci-dessus générera la sortie suivante.
[ 1.0+0.j 2.0+0.j 1.0+0.j -1.0+0.j 1.5+0.j ]le scipy.fftpackLe module permet de calculer des transformées de Fourier rapides. À titre d'illustration, un signal d'entrée (bruyant) peut ressembler à ceci:
import numpy as np
time_step = 0.02
period = 5.
time_vec = np.arange(0, 20, time_step)
sig = np.sin(2 * np.pi / period * time_vec) + 0.5 *np.random.randn(time_vec.size)
print sig.sizeNous créons un signal avec un pas de temps de 0,02 seconde. La dernière instruction imprime la taille du signal sig. La sortie serait la suivante -
1000Nous ne connaissons pas la fréquence du signal; on ne connaît que le pas de temps d'échantillonnage du signal sig. Le signal est supposé provenir d'une fonction réelle, donc la transformée de Fourier sera symétrique. lescipy.fftpack.fftfreq() la fonction générera les fréquences d'échantillonnage et scipy.fftpack.fft() va calculer la transformée de Fourier rapide.
Comprenons cela à l'aide d'un exemple.
from scipy import fftpack
sample_freq = fftpack.fftfreq(sig.size, d = time_step)
sig_fft = fftpack.fft(sig)
print sig_fftLe programme ci-dessus générera la sortie suivante.
array([
25.45122234 +0.00000000e+00j, 6.29800973 +2.20269471e+00j,
11.52137858 -2.00515732e+01j, 1.08111300 +1.35488579e+01j,
…….])Transformation discrète en cosinus
UNE Discrete Cosine Transform (DCT)exprime une séquence finie de points de données en termes d'une somme de fonctions cosinus oscillant à différentes fréquences. SciPy fournit un DCT avec la fonctiondct et un IDCT correspondant avec la fonction idct. Prenons l'exemple suivant.
from scipy.fftpack import dct
print dct(np.array([4., 3., 5., 10., 5., 3.]))Le programme ci-dessus générera la sortie suivante.
array([ 60., -3.48476592, -13.85640646, 11.3137085, 6., -6.31319305])La transformée cosinus discrète inverse reconstruit une séquence à partir de ses coefficients de transformée cosinus discrète (DCT). La fonction idct est l'inverse de la fonction dct. Comprenons cela avec l'exemple suivant.
from scipy.fftpack import dct
print idct(np.array([4., 3., 5., 10., 5., 3.]))Le programme ci-dessus générera la sortie suivante.
array([ 39.15085889, -20.14213562, -6.45392043, 7.13341236,
8.14213562, -3.83035081])Lorsqu'une fonction ne peut pas être intégrée analytiquement, ou est très difficile à intégrer analytiquement, on se tourne généralement vers des méthodes d'intégration numériques. SciPy a un certain nombre de routines pour effectuer l'intégration numérique. La plupart d'entre eux se trouvent dans le mêmescipy.integratebibliothèque. Le tableau suivant répertorie certaines fonctions couramment utilisées.
| Sr No. | Description de la fonction |
|---|---|
| 1 | quad Intégration unique |
| 2 | dblquad Double intégration |
| 3 | tplquad Triple intégration |
| 4 | nquad Intégration multiple multipliée par n |
| 5 | fixed_quad Quadrature gaussienne, ordre n |
| 6 | quadrature Quadrature gaussienne à tolérance |
| sept | romberg Intégration Romberg |
| 8 | trapz Règle trapézoïdale |
| 9 | cumtrapz Règle trapézoïdale pour calculer l'intégrale de manière cumulative |
| dix | simps La règle de Simpson |
| 11 | romb Intégration Romberg |
| 12 | polyint Intégration polynomiale analytique (NumPy) |
| 13 | poly1d Fonction d'aide pour polyint (NumPy) |
Intégrales simples
La fonction Quad est le cheval de bataille des fonctions d'intégration de SciPy. L'intégration numérique est parfois appeléequadrature, d'où le nom. C'est normalement le choix par défaut pour effectuer des intégrales uniques d'une fonction f (x) sur une plage fixe donnée de a à b.
$$\int_{a}^{b} f(x)dx$$
La forme générale du quad est scipy.integrate.quad(f, a, b), Où «f» est le nom de la fonction à intégrer. Alors que «a» et «b» sont respectivement les limites inférieure et supérieure. Voyons un exemple de la fonction gaussienne, intégrée sur une plage de 0 et 1.
Il faut d'abord définir la fonction → $f(x) = e^{-x^2}$ , cela peut être fait à l'aide d'une expression lambda, puis appeler la méthode quad sur cette fonction.
import scipy.integrate
from numpy import exp
f= lambda x:exp(-x**2)
i = scipy.integrate.quad(f, 0, 1)
print iLe programme ci-dessus générera la sortie suivante.
(0.7468241328124271, 8.291413475940725e-15)La fonction quad renvoie les deux valeurs, dans lesquelles le premier nombre est la valeur de l'intégrale et la seconde valeur est l'estimation de l'erreur absolue dans la valeur de l'intégrale.
Note- Puisque quad requiert la fonction comme premier argument, nous ne pouvons pas passer directement exp comme argument. La fonction Quad accepte l'infini positif et négatif comme limites. La fonction Quad peut intégrer des fonctions NumPy standard prédéfinies d'une seule variable, telles que exp, sin et cos.
Intégrales multiples
Les mécanismes de double et triple intégration ont été intégrés dans les fonctions dblquad, tplquad et nquad. Ces fonctions intègrent respectivement quatre ou six arguments. Les limites de toutes les intégrales internes doivent être définies comme des fonctions.
Intégrales doubles
La forme générale de dblquadest scipy.integrate.dblquad (func, a, b, gfun, hfun). Où, func est le nom de la fonction à intégrer, 'a' et 'b' sont les limites inférieure et supérieure de la variable x, respectivement, tandis que gfun et hfun sont les noms des fonctions qui définissent les limites inférieure et supérieure de la variable y.
A titre d'exemple, effectuons la méthode de la double intégrale.
$$\int_{0}^{1/2} dy \int_{0}^{\sqrt{1-4y^2}} 16xy \:dx$$
Nous définissons les fonctions f, g et h à l'aide des expressions lambda. Notez que même si g et h sont des constantes, comme elles peuvent l'être dans de nombreux cas, elles doivent être définies comme des fonctions, comme nous l'avons fait ici pour la limite inférieure.
import scipy.integrate
from numpy import exp
from math import sqrt
f = lambda x, y : 16*x*y
g = lambda x : 0
h = lambda y : sqrt(1-4*y**2)
i = scipy.integrate.dblquad(f, 0, 0.5, g, h)
print iLe programme ci-dessus générera la sortie suivante.
(0.5, 1.7092350012594845e-14)En plus des routines décrites ci-dessus, scipy.integrate a un certain nombre d'autres routines d'intégration, y compris nquad, qui effectue une intégration multiple multipliée par n, ainsi que d'autres routines qui implémentent divers algorithmes d'intégration. Cependant, quad et dblquad répondront à la plupart de nos besoins d'intégration numérique.
Dans ce chapitre, nous expliquerons comment l'interpolation aide dans SciPy.
Qu'est-ce que l'interpolation?
L'interpolation est le processus de recherche d'une valeur entre deux points sur une ligne ou une courbe. Pour nous aider à nous souvenir de ce que cela signifie, nous devrions penser à la première partie du mot «inter» comme signifiant «entrer», ce qui nous rappelle de regarder «à l'intérieur» des données que nous avions à l'origine. Cet outil, l'interpolation, n'est pas seulement utile dans les statistiques, mais est également utile dans la science, les affaires ou lorsqu'il est nécessaire de prédire des valeurs comprises dans deux points de données existants.
Créons quelques données et voyons comment cette interpolation peut être effectuée en utilisant le scipy.interpolate paquet.
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print x,yLe programme ci-dessus générera la sortie suivante.
(
array([0., 0.36363636, 0.72727273, 1.09090909, 1.45454545, 1.81818182,
2.18181818, 2.54545455, 2.90909091, 3.27272727, 3.63636364, 4.]),
array([-0.65364362, -0.61966189, -0.51077021, -0.31047698, -0.00715476,
0.37976236, 0.76715099, 0.99239518, 0.85886263, 0.27994201,
-0.52586509, -0.99582185])
)Maintenant, nous avons deux tableaux. En supposant que ces deux tableaux sont les deux dimensions des points dans l'espace, traçons en utilisant le programme suivant et voyons à quoi ils ressemblent.
plt.plot(x, y,’o’)
plt.show()Le programme ci-dessus générera la sortie suivante.
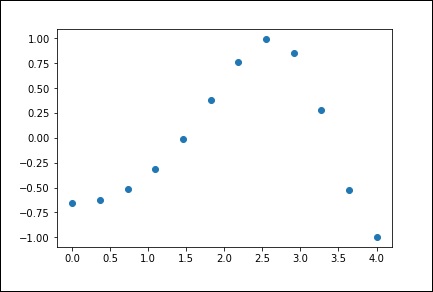
Interpolation 1D
La classe interp1d dans scipy.interpolate est une méthode pratique pour créer une fonction basée sur des points de données fixes, qui peut être évaluée n'importe où dans le domaine défini par les données données à l'aide d'une interpolation linéaire.
En utilisant les données ci-dessus, créons une fonction d'interpolation et dessinons un nouveau graphe interpolé.
f1 = interp1d(x, y,kind = 'linear')
f2 = interp1d(x, y, kind = 'cubic')En utilisant la fonction interp1d, nous avons créé deux fonctions f1 et f2. Ces fonctions, pour une entrée donnée, x renvoie y. Le troisième type de variable représente le type de la technique d'interpolation. «Linéaire», «Le plus proche», «Zéro», «Slinear», «Quadratic», «Cubic» sont quelques techniques d'interpolation.
Maintenant, créons une nouvelle entrée de plus de longueur pour voir la nette différence d'interpolation. Nous utiliserons la même fonction des anciennes données sur les nouvelles données.
xnew = np.linspace(0, 4,30)
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')
plt.show()Le programme ci-dessus générera la sortie suivante.
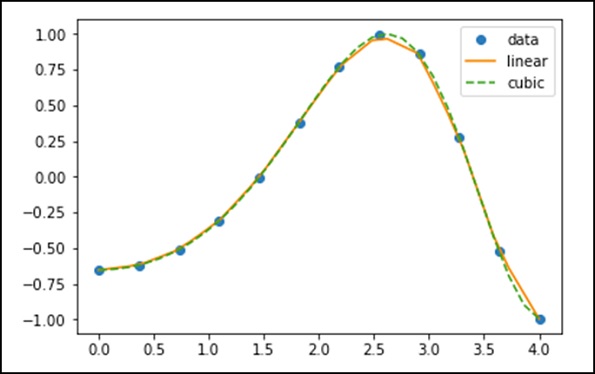
Cannelures
Pour dessiner des courbes lisses à travers des points de données, les dessinateurs utilisaient autrefois de fines bandes flexibles de bois, de caoutchouc dur, de métal ou de plastique appelées cannelures mécaniques. Pour utiliser une spline mécanique, des broches ont été placées à une sélection judicieuse de points le long d'une courbe dans une conception, puis la spline a été pliée, de sorte qu'elle touche chacune de ces broches.
Clairement, avec cette construction, la spline interpole la courbe au niveau de ces broches. Il peut être utilisé pour reproduire la courbe dans d'autres dessins. Les points où se trouvent les broches sont appelés nœuds. Nous pouvons changer la forme de la courbe définie par la spline en ajustant l'emplacement des nœuds.
Spline univariée
La spline de lissage unidimensionnelle s'adapte à un ensemble donné de points de données. La classe UnivariateSpline dans scipy.interpolate est une méthode pratique pour créer une fonction, basée sur la classe de points de données fixes - scipy.interpolate.UnivariateSpline (x, y, w = None, bbox = [None, None], k = 3, s = Aucun, ext = 0, check_finite = False).
Parameters - Voici les paramètres d'une spline univariée.
Cela ajuste une spline y = spl (x) de degré k aux données x, y fournies.
'w' - Spécifie les poids pour l'ajustement de spline. Doit être positif. Si aucun (par défaut), les poids sont tous égaux.
's' - Spécifie le nombre de nœuds en spécifiant une condition de lissage.
'k' - Degré de la spline de lissage. Doit être <= 5. La valeur par défaut est k = 3, une spline cubique.
Ext - Contrôle le mode d'extrapolation pour les éléments qui ne sont pas dans l'intervalle défini par la séquence de nœuds.
si ext = 0 ou 'extrapolate', renvoie la valeur extrapolée.
si ext = 1 ou 'zéro', renvoie 0
si ext = 2 ou 'rise', déclenche une ValueError
si ext = 3 de 'const', renvoie la valeur limite.
check_finite - Indique s'il faut vérifier que les tableaux d'entrée ne contiennent que des nombres finis.
Prenons l'exemple suivant.
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()Utilisez la valeur par défaut pour le paramètre de lissage.
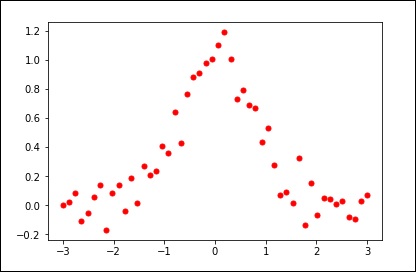
spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()Modifiez manuellement la quantité de lissage.
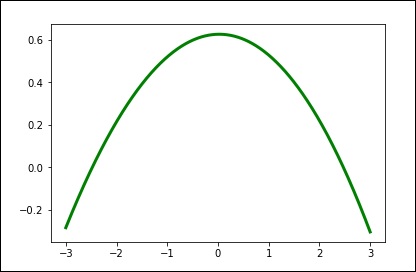
spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()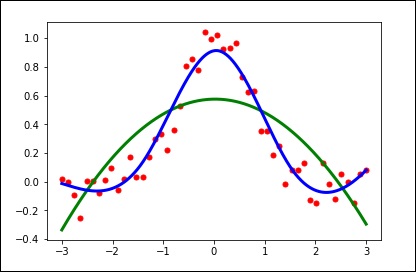
Le package Scipy.io (entrée et sortie) fournit un large éventail de fonctions pour contourner différents formats de fichiers. Certains de ces formats sont -
- Matlab
- IDL
- Marché Matrix
- Wave
- Arff
- Netcdf, etc.
Laissez-nous discuter en détail des formats de fichiers les plus couramment utilisés -
MATLAB
Voici les fonctions utilisées pour charger et enregistrer un fichier .mat.
| Sr. No. | Description de la fonction |
|---|---|
| 1 | loadmat Charge un fichier MATLAB |
| 2 | savemat Enregistre un fichier MATLAB |
| 3 | whosmat Répertorie les variables dans un fichier MATLAB |
Prenons l'exemple suivant.
import scipy.io as sio
import numpy as np
#Save a mat file
vect = np.arange(10)
sio.savemat('array.mat', {'vect':vect})
#Now Load the File
mat_file_content = sio.loadmat(‘array.mat’)
Print mat_file_contentLe programme ci-dessus générera la sortie suivante.
{
'vect': array([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]]), '__version__': '1.0',
'__header__': 'MATLAB 5.0 MAT-file Platform: posix, Created on: Sat Sep 30
09:49:32 2017', '__globals__': []
}Nous pouvons voir le tableau avec les informations Meta. Si nous voulons inspecter le contenu d'un fichier MATLAB sans lire les données en mémoire, utilisez lewhosmat command comme indiqué ci-dessous.
import scipy.io as sio
mat_file_content = sio.whosmat(‘array.mat’)
print mat_file_contentLe programme ci-dessus générera la sortie suivante.
[('vect', (1, 10), 'int64')]SciPy est construit en utilisant l'optimisé ATLAS LAPACK et BLASbibliothèques. Il a des capacités d'algèbre linéaire très rapides. Toutes ces routines d'algèbre linéaire attendent un objet qui peut être converti en un tableau bidimensionnel. La sortie de ces routines est également un tableau à deux dimensions.
SciPy.linalg contre NumPy.linalg
Un scipy.linalg contient toutes les fonctions qui se trouvent dans numpy.linalg. De plus, scipy.linalg a également d'autres fonctions avancées qui ne sont pas dans numpy.linalg. Un autre avantage de l'utilisation de scipy.linalg par rapport à numpy.linalg est qu'il est toujours compilé avec le support BLAS / LAPACK, alors que pour NumPy c'est facultatif. Par conséquent, la version SciPy peut être plus rapide en fonction de la façon dont NumPy a été installé.
Équations linéaires
le scipy.linalg.solve fonction résout l'équation linéaire a * x + b * y = Z, pour les valeurs inconnues x, y.
À titre d'exemple, supposons que l'on souhaite résoudre les équations simultanées suivantes.
x + 3y + 5z = 10
2x + 5y + z = 8
2x + 3y + 8z = 3
Pour résoudre l'équation ci-dessus pour les valeurs x, y, z, nous pouvons trouver le vecteur de solution en utilisant une matrice inverse comme indiqué ci-dessous.
$$\begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 1 & 3 & 5\\ 2 & 5 & 1\\ 2 & 3 & 8 \end{bmatrix}^{-1} \begin{bmatrix} 10\\ 8\\ 3 \end{bmatrix} = \frac{1}{25} \begin{bmatrix} -232\\ 129\\ 19 \end{bmatrix} = \begin{bmatrix} -9.28\\ 5.16\\ 0.76 \end{bmatrix}.$$
Cependant, il est préférable d'utiliser le linalg.solve commande, qui peut être plus rapide et plus stable numériquement.
La fonction de résolution prend deux entrées «a» et «b» dans lesquelles «a» représente les coefficients et «b» représente la valeur de droite respective et renvoie le tableau de solution.
Prenons l'exemple suivant.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy arrays
a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])
b = np.array([2, 4, -1])
#Passing the values to the solve function
x = linalg.solve(a, b)
#printing the result array
print xLe programme ci-dessus générera la sortie suivante.
array([ 2., -2., 9.])Trouver un déterminant
Le déterminant d'une matrice carrée A est souvent noté | A | et est une quantité souvent utilisée en algèbre linéaire. Dans SciPy, cela est calculé à l'aide dudet()fonction. Il prend une matrice en entrée et renvoie une valeur scalaire.
Prenons l'exemple suivant.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the det function
x = linalg.det(A)
#printing the result
print xLe programme ci-dessus générera la sortie suivante.
-2.0Valeurs propres et vecteurs propres
Le problème des valeurs propres-vecteurs propres est l'une des opérations d'algèbre linéaire les plus couramment utilisées. On peut trouver les valeurs propres (λ) et les vecteurs propres correspondants (v) d'une matrice carrée (A) en considérant la relation suivante -
Av = λv
scipy.linalg.eigcalcule les valeurs propres à partir d'un problème de valeurs propres ordinaire ou généralisé. Cette fonction renvoie les valeurs propres et les vecteurs propres.
Prenons l'exemple suivant.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
A = np.array([[1,2],[3,4]])
#Passing the values to the eig function
l, v = linalg.eig(A)
#printing the result for eigen values
print l
#printing the result for eigen vectors
print vLe programme ci-dessus générera la sortie suivante.
array([-0.37228132+0.j, 5.37228132+0.j]) #--Eigen Values
array([[-0.82456484, -0.41597356], #--Eigen Vectors
[ 0.56576746, -0.90937671]])Décomposition en valeurs singulières
Une décomposition en valeurs singulières (SVD) peut être considérée comme une extension du problème des valeurs propres aux matrices qui ne sont pas carrées.
le scipy.linalg.svd factorise la matrice 'a' en deux matrices unitaires 'U' et 'Vh' et un tableau 1-D 's' de valeurs singulières (réelles, non négatives) telles que a == U * S * Vh, où 'S 'est une matrice de zéros de forme appropriée avec le' s 'diagonal principal.
Prenons l'exemple suivant.
#importing the scipy and numpy packages
from scipy import linalg
import numpy as np
#Declaring the numpy array
a = np.random.randn(3, 2) + 1.j*np.random.randn(3, 2)
#Passing the values to the eig function
U, s, Vh = linalg.svd(a)
# printing the result
print U, Vh, sLe programme ci-dessus générera la sortie suivante.
(
array([
[ 0.54828424-0.23329795j, -0.38465728+0.01566714j,
-0.18764355+0.67936712j],
[-0.27123194-0.5327436j , -0.57080163-0.00266155j,
-0.39868941-0.39729416j],
[ 0.34443818+0.4110186j , -0.47972716+0.54390586j,
0.25028608-0.35186815j]
]),
array([ 3.25745379, 1.16150607]),
array([
[-0.35312444+0.j , 0.32400401+0.87768134j],
[-0.93557636+0.j , -0.12229224-0.33127251j]
])
)Le sous-module SciPy ndimage est dédié au traitement d'images. Ici, ndimage signifie une image à n dimensions.
Certaines des tâches les plus courantes du traitement d'image sont les suivantes: & miuns;
- Entrée / sortie, affichage des images
- Manipulations de base - Recadrage, retournement, rotation, etc.
- Filtrage d'image - suppression du bruit, accentuation, etc.
- Segmentation d'image - étiquetage des pixels correspondant à différents objets
- Classification
- Extraction de caractéristiques
- Registration
Voyons comment certains d'entre eux peuvent être atteints à l'aide de SciPy.
Ouverture et écriture dans des fichiers image
le misc packagedans SciPy est livré avec quelques images. Nous utilisons ces images pour apprendre les manipulations d'images. Prenons l'exemple suivant.
from scipy import misc
f = misc.face()
misc.imsave('face.png', f) # uses the Image module (PIL)
import matplotlib.pyplot as plt
plt.imshow(f)
plt.show()Le programme ci-dessus générera la sortie suivante.

Toutes les images dans son format brut sont la combinaison de couleurs représentées par les nombres dans le format matriciel. Une machine comprend et manipule les images en se basant uniquement sur ces nombres. RVB est un moyen de représentation populaire.
Voyons les informations statistiques de l'image ci-dessus.
from scipy import misc
face = misc.face(gray = False)
print face.mean(), face.max(), face.min()Le programme ci-dessus générera la sortie suivante.
110.16274388631184, 255, 0Maintenant, nous savons que l'image est faite de nombres, donc tout changement dans la valeur du nombre altère l'image d'origine. Réalisons quelques transformations géométriques sur l'image. L'opération géométrique de base est le recadrage
from scipy import misc
face = misc.face(gray = True)
lx, ly = face.shape
# Cropping
crop_face = face[lx / 4: - lx / 4, ly / 4: - ly / 4]
import matplotlib.pyplot as plt
plt.imshow(crop_face)
plt.show()Le programme ci-dessus générera la sortie suivante.
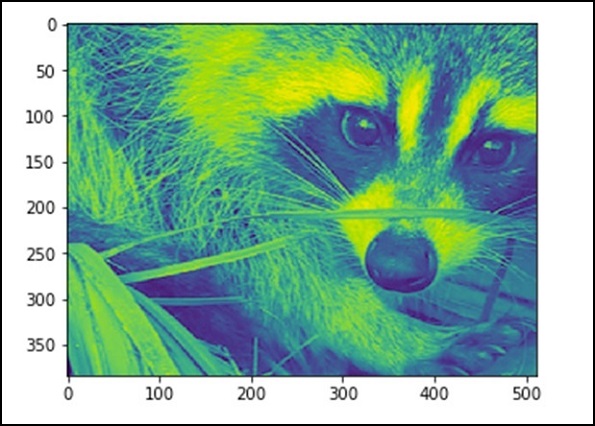
Nous pouvons également effectuer certaines opérations de base telles que retourner l'image comme décrit ci-dessous.
# up <-> down flip
from scipy import misc
face = misc.face()
flip_ud_face = np.flipud(face)
import matplotlib.pyplot as plt
plt.imshow(flip_ud_face)
plt.show()Le programme ci-dessus générera la sortie suivante.

Outre cela, nous avons le rotate() function, qui fait pivoter l'image avec un angle spécifié.
# rotation
from scipy import misc,ndimage
face = misc.face()
rotate_face = ndimage.rotate(face, 45)
import matplotlib.pyplot as plt
plt.imshow(rotate_face)
plt.show()Le programme ci-dessus générera la sortie suivante.
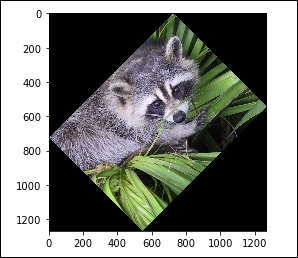
Filtres
Voyons comment les filtres aident au traitement d'image.
Qu'est-ce que le filtrage dans le traitement d'image?
Le filtrage est une technique permettant de modifier ou d'améliorer une image. Par exemple, vous pouvez filtrer une image pour mettre en valeur certaines fonctionnalités ou supprimer d'autres fonctionnalités. Les opérations de traitement d'image implémentées avec le filtrage incluent le lissage, la netteté et l'amélioration des contours.
Le filtrage est une opération de voisinage, dans laquelle la valeur de n'importe quel pixel donné dans l'image de sortie est déterminée en appliquant un algorithme aux valeurs des pixels au voisinage du pixel d'entrée correspondant. Faisons maintenant quelques opérations à l'aide de SciPy ndimage.
Flou
Le flou est largement utilisé pour réduire le bruit de l'image. Nous pouvons effectuer une opération de filtrage et voir le changement dans l'image. Prenons l'exemple suivant.
from scipy import misc
face = misc.face()
blurred_face = ndimage.gaussian_filter(face, sigma=3)
import matplotlib.pyplot as plt
plt.imshow(blurred_face)
plt.show()Le programme ci-dessus générera la sortie suivante.

La valeur sigma indique le niveau de flou sur une échelle de cinq. Nous pouvons voir le changement sur la qualité de l'image en réglant la valeur sigma. Pour plus de détails sur le flou, cliquez sur → Tutoriel DIP (Digital Image Processing).
Détection des bords
Voyons comment la détection des contours aide au traitement de l'image.
Qu'est-ce que la détection des contours?
La détection des contours est une technique de traitement d'image pour trouver les limites des objets dans les images. Il fonctionne en détectant les discontinuités de luminosité. La détection des contours est utilisée pour la segmentation d'image et l'extraction de données dans des domaines tels que le traitement d'image, la vision par ordinateur et la vision industrielle.
Les algorithmes de détection de bord les plus couramment utilisés incluent
- Sobel
- Canny
- Prewitt
- Roberts
- Méthodes de logique floue
Prenons l'exemple suivant.
import scipy.ndimage as nd
import numpy as np
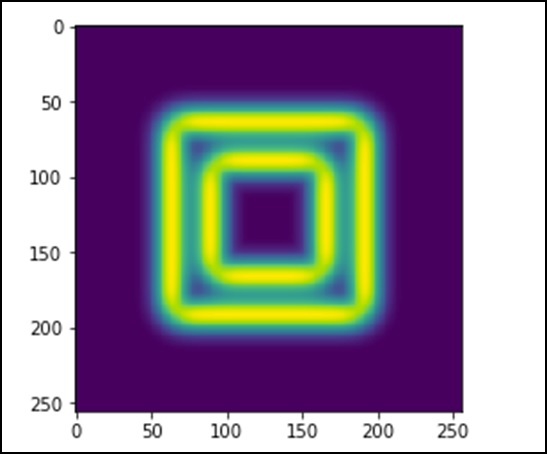
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
import matplotlib.pyplot as plt
plt.imshow(im)
plt.show()Le programme ci-dessus générera la sortie suivante.

L'image ressemble à un bloc carré de couleurs. Maintenant, nous allons détecter les bords de ces blocs colorés. Ici, ndimage fournit une fonction appeléeSobelpour effectuer cette opération. Alors que NumPy fournit leHypot fonction pour combiner les deux matrices résultantes en une seule.
Prenons l'exemple suivant.
import scipy.ndimage as nd
import matplotlib.pyplot as plt
im = np.zeros((256, 256))
im[64:-64, 64:-64] = 1
im[90:-90,90:-90] = 2
im = ndimage.gaussian_filter(im, 8)
sx = ndimage.sobel(im, axis = 0, mode = 'constant')
sy = ndimage.sobel(im, axis = 1, mode = 'constant')
sob = np.hypot(sx, sy)
plt.imshow(sob)
plt.show()Le programme ci-dessus générera la sortie suivante.
le scipy.optimize packagefournit plusieurs algorithmes d'optimisation couramment utilisés. Ce module contient les aspects suivants -
Minimisation sans contrainte et contrainte de fonctions scalaires multivariées (minimiser ()) à l'aide de divers algorithmes (par exemple BFGS, Nelder-Mead simplex, Newton Conjugate Gradient, COBYLA ou SLSQP)
Routines d'optimisation globale (force brute) (par exemple, anneal (), bassinhopping ())
Minimisation des moindres carrés (algorithmes de minimisation des moindres carrés ()) et d'ajustement de courbe (curve_fit ())
Minimiseurs de fonctions scalaires univariées (minimiser_scalar ()) et recherche de racines (newton ())
Solveurs de systèmes d'équations multivariées (root ()) utilisant une variété d'algorithmes (par exemple, des méthodes hybrides Powell, Levenberg-Marquardt ou à grande échelle comme Newton-Krylov)
Minimisation sans contrainte et contrainte des fonctions scalaires multivariées
le minimize() function fournit une interface commune aux algorithmes de minimisation sans contrainte et contrainte pour les fonctions scalaires multivariées dans scipy.optimize. Pour démontrer la fonction de minimisation, considérons le problème de minimisation de la fonction de Rosenbrock des variables NN -
$$f(x) = \sum_{i = 1}^{N-1} \:100(x_i - x_{i-1}^{2})$$
La valeur minimale de cette fonction est 0, ce qui est obtenu lorsque xi = 1.
Algorithme Nelder – Mead Simplex
Dans l'exemple suivant, la routine minimiser () est utilisée avec le Nelder-Mead simplex algorithm (method = 'Nelder-Mead')(sélectionné via le paramètre de méthode). Prenons l'exemple suivant.
import numpy as np
from scipy.optimize import minimize
def rosen(x):
x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])
res = minimize(rosen, x0, method='nelder-mead')
print(res.x)Le programme ci-dessus générera la sortie suivante.
[7.93700741e+54 -5.41692163e+53 6.28769150e+53 1.38050484e+55 -4.14751333e+54]L'algorithme simplex est probablement le moyen le plus simple de minimiser une fonction assez bien comportée. Il ne nécessite que des évaluations de fonctions et constitue un bon choix pour les problèmes de minimisation simples. Cependant, comme il n'utilise aucune évaluation de gradient, la recherche du minimum peut prendre plus de temps.
Un autre algorithme d'optimisation qui n'a besoin que d'appels de fonction pour trouver le minimum est le Powell‘s method, qui est disponible en définissant method = 'powell' dans la fonction minimiser ().
Moindres carrés
Résolvez un problème de moindres carrés non linéaire avec des limites sur les variables. Étant donné les résidus f (x) (une fonction réelle à m dimensions de n variables réelles) et la fonction de perte rho (s) (une fonction scalaire), les moindres carrés trouvent un minimum local de la fonction de coût F (x). Prenons l'exemple suivant.
Dans cet exemple, nous trouvons un minimum de la fonction Rosenbrock sans bornes sur les variables indépendantes.
#Rosenbrock Function
def fun_rosenbrock(x):
return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(fun_rosenbrock, input)
print resNotez que nous ne fournissons que le vecteur des résidus. L'algorithme construit la fonction de coût comme une somme des carrés des résidus, ce qui donne la fonction de Rosenbrock. Le minimum exact est à x = [1.0,1.0].
Le programme ci-dessus générera la sortie suivante.
active_mask: array([ 0., 0.])
cost: 9.8669242910846867e-30
fun: array([ 4.44089210e-15, 1.11022302e-16])
grad: array([ -8.89288649e-14, 4.44089210e-14])
jac: array([[-20.00000015,10.],[ -1.,0.]])
message: '`gtol` termination condition is satisfied.'
nfev: 3
njev: 3
optimality: 8.8928864934219529e-14
status: 1
success: True
x: array([ 1., 1.])Recherche de racine
Laissez-nous comprendre comment la recherche de racine aide dans SciPy.
Fonctions scalaires
Si l'on a une équation à une seule variable, il existe quatre algorithmes de recherche de racine différents, qui peuvent être essayés. Chacun de ces algorithmes nécessite les extrémités d'un intervalle dans lequel une racine est attendue (car la fonction change de signe). En général,brentq est le meilleur choix, mais les autres méthodes peuvent être utiles dans certaines circonstances ou à des fins académiques.
Résolution en virgule fixe
Un problème étroitement lié à la recherche des zéros d'une fonction est le problème de la recherche d'un point fixe d'une fonction. Un point fixe d'une fonction est le point auquel l'évaluation de la fonction renvoie le point: g (x) = x. Clairement le point fixe deggest la racine de f (x) = g (x) −x. De manière équivalente, la racine deffest le point fixe de g (x) = f (x) + x. La routine fixed_point fournit une méthode itérative simple utilisant leAitkens sequence acceleration pour estimer le point fixe de gg, si un point de départ est donné.
Ensembles d'équations
La recherche d'une racine d'un ensemble d'équations non linéaires peut être obtenue en utilisant root() function. Plusieurs méthodes sont disponibles, parmi lesquelleshybr (par défaut) et lm, utilisent respectivement le hybrid method of Powell et le Levenberg-Marquardt method du MINPACK.
L'exemple suivant considère l'équation transcendantale à variable unique.
x2 + 2cos(x) = 0
Une racine dont peut être trouvée comme suit -
import numpy as np
from scipy.optimize import root
def func(x):
return x*2 + 2 * np.cos(x)
sol = root(func, 0.3)
print solLe programme ci-dessus générera la sortie suivante.
fjac: array([[-1.]])
fun: array([ 2.22044605e-16])
message: 'The solution converged.'
nfev: 10
qtf: array([ -2.77644574e-12])
r: array([-3.34722409])
status: 1
success: True
x: array([-0.73908513])Toutes les fonctions statistiques se trouvent dans le sous-package scipy.stats et une liste assez complète de ces fonctions peut être obtenue en utilisant info(stats)fonction. Une liste des variables aléatoires disponibles peut également être obtenue à partir dudocstringpour le sous-package stats. Ce module contient un grand nombre de distributions de probabilités ainsi qu'une bibliothèque croissante de fonctions statistiques.
Chaque distribution univariée a sa propre sous-classe comme décrit dans le tableau suivant -
| Sr. No. | Classe et description |
|---|---|
| 1 | rv_continuous Une classe générique de variable aléatoire continue destinée au sous-classement |
| 2 | rv_discrete Une classe de variable aléatoire discrète générique destinée au sous-classement |
| 3 | rv_histogram Génère une distribution donnée par un histogramme |
Variable aléatoire continue normale
Une distribution de probabilité dans laquelle la variable aléatoire X peut prendre n'importe quelle valeur est une variable aléatoire continue. Le mot-clé location (loc) spécifie la moyenne. Le mot clé scale (scale) spécifie l'écart type.
En tant qu'instance du rv_continuous classe, norm object en hérite une collection de méthodes génériques et les complète avec des détails spécifiques à cette distribution particulière.
Pour calculer le CDF en un certain nombre de points, nous pouvons passer une liste ou un tableau NumPy. Prenons l'exemple suivant.
from scipy.stats import norm
import numpy as np
print norm.cdf(np.array([1,-1., 0, 1, 3, 4, -2, 6]))Le programme ci-dessus générera la sortie suivante.
array([ 0.84134475, 0.15865525, 0.5 , 0.84134475, 0.9986501 ,
0.99996833, 0.02275013, 1. ])Pour trouver la médiane d'une distribution, nous pouvons utiliser la fonction de point de pourcentage (PPF), qui est l'inverse de la CDF. Laissez-nous comprendre en utilisant l'exemple suivant.
from scipy.stats import norm
print norm.ppf(0.5)Le programme ci-dessus générera la sortie suivante.
0.0Pour générer une séquence de variables aléatoires, nous devons utiliser l'argument de mot-clé size, qui est illustré dans l'exemple suivant.
from scipy.stats import norm
print norm.rvs(size = 5)Le programme ci-dessus générera la sortie suivante.
array([ 0.20929928, -1.91049255, 0.41264672, -0.7135557 , -0.03833048])La sortie ci-dessus n'est pas reproductible. Pour générer les mêmes nombres aléatoires, utilisez la fonction de départ.
Distribution uniforme
Une distribution uniforme peut être générée en utilisant la fonction uniforme. Prenons l'exemple suivant.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)Le programme ci-dessus générera la sortie suivante.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])Créer une distribution discrète
Générons un échantillon aléatoire et comparons les fréquences observées avec les probabilités.
Distribution binomiale
En tant qu'instance du rv_discrete class, la binom objecten hérite une collection de méthodes génériques et les complète avec des détails spécifiques à cette distribution particulière. Prenons l'exemple suivant.
from scipy.stats import uniform
print uniform.cdf([0, 1, 2, 3, 4, 5], loc = 1, scale = 4)Le programme ci-dessus générera la sortie suivante.
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])Statistiques descriptives
Les statistiques de base telles que Min, Max, Moyenne et Variance prennent le tableau NumPy comme entrée et retournent les résultats respectifs. Quelques fonctions statistiques de base disponibles dans lescipy.stats package sont décrits dans le tableau suivant.
| Sr. No. | Description de la fonction |
|---|---|
| 1 | describe() Calcule plusieurs statistiques descriptives du tableau passé |
| 2 | gmean() Calcule la moyenne géométrique le long de l'axe spécifié |
| 3 | hmean() Calcule la moyenne harmonique le long de l'axe spécifié |
| 4 | kurtosis() Calcule le kurtosis |
| 5 | mode() Renvoie la valeur modale |
| 6 | skew() Teste l'asymétrie des données |
| sept | f_oneway() Effectue une ANOVA unidirectionnelle |
| 8 | iqr() Calcule l'intervalle interquartile des données le long de l'axe spécifié |
| 9 | zscore() Calcule le score z de chaque valeur de l'échantillon, par rapport à la moyenne de l'échantillon et à l'écart type |
| dix | sem() Calcule l'erreur standard de la moyenne (ou erreur standard de mesure) des valeurs dans le tableau d'entrée |
Plusieurs de ces fonctions ont une version similaire dans le scipy.stats.mstats, qui fonctionnent pour les tableaux masqués. Comprenons cela avec l'exemple ci-dessous.
from scipy import stats
import numpy as np
x = np.array([1,2,3,4,5,6,7,8,9])
print x.max(),x.min(),x.mean(),x.var()Le programme ci-dessus générera la sortie suivante.
(9, 1, 5.0, 6.666666666666667)Test T
Comprenons comment le test T est utile dans SciPy.
ttest_1samp
Calcule le test T pour la moyenne d'UN groupe de scores. Il s'agit d'un test bilatéral pour l'hypothèse nulle que la valeur attendue (moyenne) d'un échantillon d'observations indépendantes `` a '' est égale à la moyenne de la population donnée,popmean. Prenons l'exemple suivant.
from scipy import stats
rvs = stats.norm.rvs(loc = 5, scale = 10, size = (50,2))
print stats.ttest_1samp(rvs,5.0)Le programme ci-dessus générera la sortie suivante.
Ttest_1sampResult(statistic = array([-1.40184894, 2.70158009]),
pvalue = array([ 0.16726344, 0.00945234]))Comparaison de deux échantillons
Dans les exemples suivants, il y a deux échantillons, qui peuvent provenir de la même distribution ou d'une distribution différente, et nous voulons tester si ces échantillons ont les mêmes propriétés statistiques.
ttest_ind- Calcule le test T pour les moyennes de deux échantillons indépendants de scores. Il s'agit d'un test bilatéral pour l'hypothèse nulle selon laquelle deux échantillons indépendants ont des valeurs moyennes (attendues) identiques. Ce test suppose que les populations ont des variances identiques par défaut.
Nous pouvons utiliser ce test si nous observons deux échantillons indépendants d'une population identique ou différente. Prenons l'exemple suivant.
from scipy import stats
rvs1 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
rvs2 = stats.norm.rvs(loc = 5,scale = 10,size = 500)
print stats.ttest_ind(rvs1,rvs2)Le programme ci-dessus générera la sortie suivante.
Ttest_indResult(statistic = -0.67406312233650278, pvalue = 0.50042727502272966)Vous pouvez tester la même chose avec un nouveau tableau de même longueur, mais avec une moyenne variée. Utilisez une valeur différente dansloc et testez la même chose.
CSGraph signifie Compressed Sparse Graph, qui se concentre sur les algorithmes de graphe rapide basés sur des représentations matricielles éparses.
Représentations graphiques
Pour commencer, comprenons ce qu'est un graphe clairsemé et comment il aide dans les représentations graphiques.
Qu'est-ce qu'un graphique clairsemé?
Un graphe n'est qu'un ensemble de nœuds, qui ont des liens entre eux. Les graphiques peuvent représenter presque tout - les connexions aux réseaux sociaux, où chaque nœud est une personne et est connecté à des connaissances; des images, où chaque nœud est un pixel et est connecté aux pixels voisins; des points dans une distribution de grande dimension, où chaque nœud est connecté à ses voisins les plus proches; et pratiquement tout ce que vous pouvez imaginer.
Une manière très efficace de représenter les données d'un graphe est dans une matrice creuse: appelons-la G. La matrice G est de taille N x N, et G [i, j] donne la valeur de la connexion entre le nœud 'i' et le nœud «j». Un graphe fragmenté contient principalement des zéros, c'est-à-dire que la plupart des nœuds n'ont que quelques connexions. Cette propriété s'avère être vraie dans la plupart des cas d'intérêt.
La création du sous-module de graphe clairsemé a été motivée par plusieurs algorithmes utilisés dans scikit-learn qui comprenaient les éléments suivants:
Isomap - Un algorithme d'apprentissage multiple, qui nécessite de trouver les chemins les plus courts dans un graphique.
Hierarchical clustering - Un algorithme de clustering basé sur un arbre couvrant minimum.
Spectral Decomposition - Un algorithme de projection basé sur des laplaciens à graphes clairsemés.
À titre d'exemple concret, imaginons que nous aimerions représenter le graphe non orienté suivant -
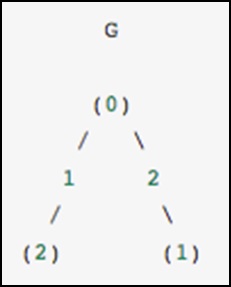
Ce graphe a trois nœuds, où les nœuds 0 et 1 sont reliés par une arête de poids 2 et les nœuds 0 et 2 sont reliés par une arête de poids 1. Nous pouvons construire les représentations denses, masquées et éparses comme le montre l'exemple suivant , en gardant à l'esprit qu'un graphe non orienté est représenté par une matrice symétrique.
G_dense = np.array([ [0, 2, 1],
[2, 0, 0],
[1, 0, 0] ])
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix
G_sparse = csr_matrix(G_dense)
print G_sparse.dataLe programme ci-dessus générera la sortie suivante.
array([2, 1, 2, 1])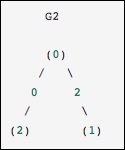
Ceci est identique au graphique précédent, sauf que les nœuds 0 et 2 sont reliés par une arête de poids nul. Dans ce cas, la représentation dense ci-dessus conduit à des ambiguïtés - comment les non-arêtes peuvent être représentées, si zéro est une valeur significative. Dans ce cas, une représentation masquée ou clairsemée doit être utilisée pour éliminer l'ambiguïté.
Prenons l'exemple suivant.
from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
[np.inf, 2, 0 ],
[2, np.inf, np.inf],
[0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.dataLe programme ci-dessus générera la sortie suivante.
array([ 2., 0., 2., 0.])Echelles de mots utilisant des graphiques épars
Word ladders est un jeu inventé par Lewis Carroll, dans lequel les mots sont liés en changeant une seule lettre à chaque étape. Par exemple -
APE → APT → AIT → BIT → BIG → BAG → MAG → MAN
Ici, nous sommes passés de "APE" à "MAN" en sept étapes, en changeant une lettre à chaque fois. La question est - Pouvons-nous trouver un chemin plus court entre ces mots en utilisant la même règle? Ce problème est naturellement exprimé sous la forme d'un problème de graphe clairsemé. Les nœuds correspondront à des mots individuels, et nous créerons des connexions entre des mots qui diffèrent au plus d'une lettre.
Obtenir une liste de mots
Tout d'abord, bien sûr, nous devons obtenir une liste de mots valides. J'utilise Mac et Mac a un dictionnaire de mots à l'emplacement indiqué dans le bloc de code suivant. Si vous êtes sur une architecture différente, vous devrez peut-être chercher un peu pour trouver votre dictionnaire système.
wordlist = open('/usr/share/dict/words').read().split()
print len(wordlist)Le programme ci-dessus générera la sortie suivante.
235886Nous voulons maintenant examiner les mots de longueur 3, alors sélectionnons uniquement les mots de longueur correcte. Nous éliminerons également les mots qui commencent par des majuscules (noms propres) ou contiennent des caractères non alphanumériques tels que des apostrophes et des tirets. Enfin, nous nous assurerons que tout est en minuscules pour une comparaison ultérieure.
word_list = [word for word in word_list if len(word) == 3]
word_list = [word for word in word_list if word[0].islower()]
word_list = [word for word in word_list if word.isalpha()]
word_list = map(str.lower, word_list)
print len(word_list)Le programme ci-dessus générera la sortie suivante.
1135Maintenant, nous avons une liste de 1135 mots valides de trois lettres (le nombre exact peut changer en fonction de la liste particulière utilisée). Chacun de ces mots deviendra un nœud dans notre graphe, et nous créerons des arêtes reliant les nœuds associés à chaque paire de mots, qui ne diffère que d'une lettre.
import numpy as np
word_list = np.asarray(word_list)
word_list.dtype
word_list.sort()
word_bytes = np.ndarray((word_list.size, word_list.itemsize),
dtype = 'int8',
buffer = word_list.data)
print word_bytes.shapeLe programme ci-dessus générera la sortie suivante.
(1135, 3)Nous utiliserons la distance de Hamming entre chaque point pour déterminer quelles paires de mots sont connectées. La distance de Hamming mesure la fraction d'entrées entre deux vecteurs, qui diffèrent: deux mots quelconques avec une distance de martelage égale à 1 / N1 / N, où NN est le nombre de lettres qui sont connectées dans l'échelle de mots.
from scipy.spatial.distance import pdist, squareform
from scipy.sparse import csr_matrix
hamming_dist = pdist(word_bytes, metric = 'hamming')
graph = csr_matrix(squareform(hamming_dist < 1.5 / word_list.itemsize))Lors de la comparaison des distances, nous n'utilisons pas l'égalité car cela peut être instable pour les valeurs à virgule flottante. L'inégalité produit le résultat souhaité tant que deux entrées de la liste de mots ne sont pas identiques. Maintenant que notre graphique est configuré, nous utiliserons la recherche de chemin le plus court pour trouver le chemin entre deux mots quelconques du graphique.
i1 = word_list.searchsorted('ape')
i2 = word_list.searchsorted('man')
print word_list[i1],word_list[i2]Le programme ci-dessus générera la sortie suivante.
ape, manNous devons vérifier que ceux-ci correspondent, car si les mots ne sont pas dans la liste, il y aura une erreur dans la sortie. Maintenant, tout ce dont nous avons besoin est de trouver le chemin le plus court entre ces deux indices dans le graphique. Nous utiliseronsdijkstra’s algorithme, car il nous permet de trouver le chemin pour un seul nœud.
from scipy.sparse.csgraph import dijkstra
distances, predecessors = dijkstra(graph, indices = i1, return_predecessors = True)
print distances[i2]Le programme ci-dessus générera la sortie suivante.
5.0Ainsi, nous voyons que le chemin le plus court entre «singe» et «homme» ne comporte que cinq étapes. Nous pouvons utiliser les prédécesseurs retournés par l'algorithme pour reconstruire ce chemin.
path = []
i = i2
while i != i1:
path.append(word_list[i])
i = predecessors[i]
path.append(word_list[i1])
print path[::-1]i2]Le programme ci-dessus générera la sortie suivante.
['ape', 'ope', 'opt', 'oat', 'mat', 'man']le scipy.spatial package peut calculer des triangulations, des diagrammes de Voronoï et des coques convexes d'un ensemble de points, en tirant parti du Qhull library. De plus, il contientKDTree implementations pour les requêtes de points voisins les plus proches et les utilitaires pour les calculs de distance dans diverses métriques.
Triangulations de Delaunay
Comprenons ce que sont les triangulations de Delaunay et comment elles sont utilisées dans SciPy.
Que sont les triangulations de Delaunay?
En mathématiques et en géométrie computationnelle, une triangulation de Delaunay pour un ensemble donné P de points discrets dans un plan est une triangulation DT(P) de telle sorte que cela ne sert à rien P est à l'intérieur du cercle circulaire de n'importe quel triangle dans DT (P).
Nous pouvons calculer la même chose via SciPy. Prenons l'exemple suivant.
from scipy.spatial import Delaunay
points = np.array([[0, 4], [2, 1.1], [1, 3], [1, 2]])
tri = Delaunay(points)
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices.copy())
plt.plot(points[:,0], points[:,1], 'o')
plt.show()Le programme ci-dessus générera la sortie suivante.

Points coplanaires
Comprenons ce que sont les points Coplanar et comment ils sont utilisés dans SciPy.
Que sont les points coplanaires?
Les points coplanaires sont au moins trois points situés dans le même plan. Rappelons qu'un plan est une surface plane, qui s'étend sans fin dans toutes les directions. Il est généralement présenté dans les manuels de mathématiques sous la forme d'une figure à quatre côtés.
Voyons comment nous pouvons trouver cela en utilisant SciPy. Prenons l'exemple suivant.
from scipy.spatial import Delaunay
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
print tri.coplanarLe programme ci-dessus générera la sortie suivante.
array([[4, 0, 3]], dtype = int32)Cela signifie que le point 4 réside près du triangle 0 et du sommet 3, mais n'est pas inclus dans la triangulation.
Coques convexes
Comprenons ce que sont les coques convexes et comment elles sont utilisées dans SciPy.
Que sont les coques convexes?
En mathématiques, le convex hull ou convex envelope d'un ensemble de points X dans le plan euclidien ou dans un espace euclidien (ou, plus généralement, dans un espace affine sur les réels) est le plus petit convex set qui contient X.
Prenons l'exemple suivant pour le comprendre en détail.
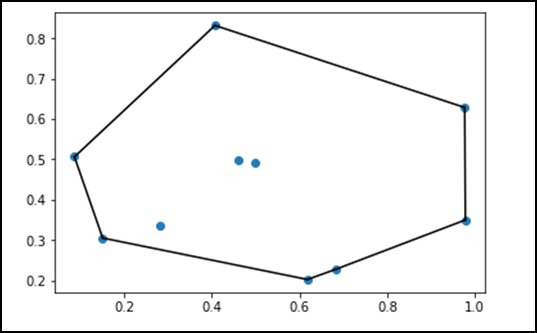
from scipy.spatial import ConvexHull
points = np.random.rand(10, 2) # 30 random points in 2-D
hull = ConvexHull(points)
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()Le programme ci-dessus générera la sortie suivante.
ODR signifie Orthogonal Distance Regression, qui est utilisé dans les études de régression. La régression linéaire de base est souvent utilisée pour estimer la relation entre les deux variablesy et x en traçant la ligne de meilleur ajustement sur le graphique.
La méthode mathématique utilisée pour cela est connue sous le nom de Least Squares, et vise à minimiser la somme de l'erreur quadratique pour chaque point. La question clé ici est de savoir comment calculer l'erreur (également appelée résidu) pour chaque point?
Dans une régression linéaire standard, le but est de prédire la valeur Y à partir de la valeur X - donc la chose sensée à faire est de calculer l'erreur dans les valeurs Y (indiquées par les lignes grises dans l'image suivante). Cependant, il est parfois plus judicieux de prendre en compte l'erreur à la fois en X et en Y (comme le montrent les lignes rouges en pointillés dans l'image suivante).
Par exemple - Lorsque vous savez que vos mesures de X sont incertaines, ou lorsque vous ne voulez pas vous concentrer sur les erreurs d'une variable par rapport à une autre.
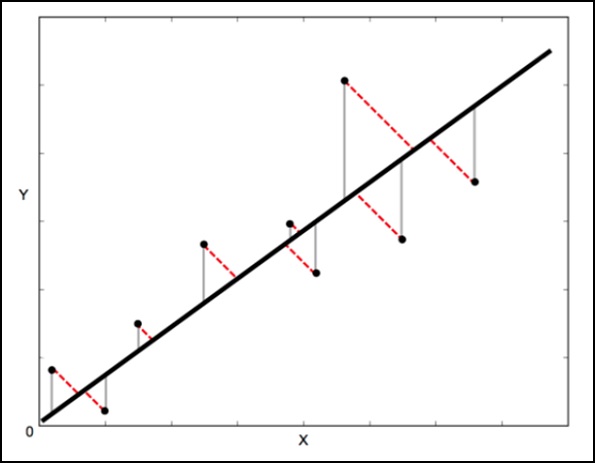
La régression de distance orthogonale (ODR) est une méthode qui peut le faire (orthogonale dans ce contexte signifie perpendiculaire - elle calcule donc les erreurs perpendiculaires à la ligne, plutôt que simplement «verticalement»).
Implémentation scipy.odr pour la régression univariée
L'exemple suivant illustre l'implémentation de scipy.odr pour la régression univariée.
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()Le programme ci-dessus générera la sortie suivante.
Beta: [ 5.51846098 -4.25744878]
Beta Std Error: [ 0.7786442 2.33126407]
Beta Covariance: [
[ 1.93150969 -4.82877433]
[ -4.82877433 17.31417201
]]
Residual Variance: 0.313892697582
Inverse Condition #: 0.146618499389
Reason(s) for Halting:
Sum of squares convergenceLes fonctions disponibles dans le package spécial sont des fonctions universelles, qui suivent la diffusion et le bouclage automatique du tableau.
Examinons quelques-unes des fonctions spéciales les plus fréquemment utilisées -
- Fonction racine cubique
- Fonction exponentielle
- Fonction exponentielle d'erreur relative
- Fonction exponentielle de la somme des journaux
- Fonction Lambert
- Fonction permutations et combinaisons
- Fonction gamma
Voyons maintenant chacune de ces fonctions en bref.
Fonction racine cubique
La syntaxe de cette fonction racine cubique est - scipy.special.cbrt (x). Cela récupérera la racine cubique élément par élément dex.
Prenons l'exemple suivant.
from scipy.special import cbrt
res = cbrt([10, 9, 0.1254, 234])
print resLe programme ci-dessus générera la sortie suivante.
[ 2.15443469 2.08008382 0.50053277 6.16224015]Fonction exponentielle
La syntaxe de la fonction exponentielle est - scipy.special.exp10 (x). Cela calculera 10 ** x élément par élément.
Prenons l'exemple suivant.
from scipy.special import exp10
res = exp10([2, 9])
print resLe programme ci-dessus générera la sortie suivante.
[1.00000000e+02 1.00000000e+09]Fonction exponentielle d'erreur relative
La syntaxe de cette fonction est - scipy.special.exprel (x). Il génère l'erreur relative exponentielle, (exp (x) - 1) / x.
Quand xest proche de zéro, exp (x) est proche de 1, de sorte que le calcul numérique de exp (x) - 1 peut souffrir d'une perte de précision catastrophique. Ensuite, exprel (x) est implémenté pour éviter la perte de précision, qui se produit lorsquex est proche de zéro.
Prenons l'exemple suivant.
from scipy.special import exprel
res = exprel([-0.25, -0.1, 0, 0.1, 0.25])
print resLe programme ci-dessus générera la sortie suivante.
[0.88479687 0.95162582 1. 1.05170918 1.13610167]Fonction exponentielle de la somme des journaux
La syntaxe de cette fonction est - scipy.special.logsumexp (x). Il aide à calculer le journal de la somme des exponentielles des éléments d'entrée.
Prenons l'exemple suivant.
from scipy.special import logsumexp
import numpy as np
a = np.arange(10)
res = logsumexp(a)
print resLe programme ci-dessus générera la sortie suivante.
9.45862974443Fonction Lambert
La syntaxe de cette fonction est - scipy.special.lambertw (x). Elle est également appelée fonction Lambert W. La fonction Lambert W W (z) est définie comme la fonction inverse de w * exp (w). En d'autres termes, la valeur de W (z) est telle que z = W (z) * exp (W (z)) pour tout nombre complexe z.
La fonction Lambert W est une fonction à valeurs multiples avec une infinité de branches. Chaque branche donne une solution distincte de l'équation z = w exp (w). Ici, les branches sont indexées par l'entier k.
Prenons l'exemple suivant. Ici, la fonction Lambert W est l'inverse de w exp (w).
from scipy.special import lambertw
w = lambertw(1)
print w
print w * np.exp(w)Le programme ci-dessus générera la sortie suivante.
(0.56714329041+0j)
(1+0j)Permutations et combinaisons
Discutons séparément des permutations et des combinaisons pour les comprendre clairement.
Combinations- La syntaxe de la fonction de combinaisons est - scipy.special.comb (N, k). Prenons l'exemple suivant -
from scipy.special import comb
res = comb(10, 3, exact = False,repetition=True)
print resLe programme ci-dessus générera la sortie suivante.
220.0Note- Les arguments de tableau ne sont acceptés que pour le cas exact = Faux. Si k> N, N <0 ou k <0, alors un 0 est renvoyé.
Permutations- La syntaxe de la fonction de combinaisons est - scipy.special.perm (N, k). Permutations de N choses prises k à la fois, c'est-à-dire k-permutations de N. Ceci est également connu sous le nom de «permutations partielles».
Prenons l'exemple suivant.
from scipy.special import perm
res = perm(10, 3, exact = True)
print resLe programme ci-dessus générera la sortie suivante.
720Fonction gamma
La fonction gamma est souvent appelée factorielle généralisée puisque z * gamma (z) = gamma (z + 1) et gamma (n + 1) = n !, pour un entier naturel 'n'.
La syntaxe de la fonction de combinaisons est - scipy.special.gamma (x). Permutations de N choses prises k à la fois, c'est-à-dire k-permutations de N. Ceci est également connu sous le nom de «permutations partielles».
La syntaxe de la fonction de combinaisons est - scipy.special.gamma (x). Permutations de N choses prises k à la fois, c'est-à-dire k-permutations de N. Ceci est également connu sous le nom de «permutations partielles».
from scipy.special import gamma
res = gamma([0, 0.5, 1, 5])
print resLe programme ci-dessus générera la sortie suivante.
[inf 1.77245385 1. 24.]