SymPy - Guide rapide
SymPy est une bibliothèque Python pour effectuer des calculs symboliques. C'est uncomputer algebra system(CAS) qui peut être utilisé soit en tant qu'application autonome, soit en tant que bibliothèque pour d'autres applications. Sa session en direct est également disponible surhttps://live.sympy.org/. Puisqu'il s'agit d'une pure bibliothèque Python, elle peut être utilisée comme mode interactif et comme application de programmation. SymPy est maintenant devenu une bibliothèque symbolique populaire pour l'écosystème scientifique Python.
SymPy dispose d'un large éventail de fonctionnalités applicables dans le domaine de l'arithmétique symbolique de base, du calcul, de l'algèbre, des mathématiques discrètes, de la physique quantique, etc. SymPy est capable de formater les résultats dans divers formats, y compris LaTeX, MathML, etc. SymPy est distribué sous Nouvelle licence BSD. Une équipe de développeurs dirigée parOndřej Čertík et Aaron Meurer a publié la première version de SymPy en 2007. Sa version actuelle est la 1.5.1.
Certains des domaines d'application de SymPy sont -
- Polynomials
- Calculus
- Maths discrets
- Matrices
- Geometry
- Plotting
- Physics
- Statistics
- Combinatorics
SymPy a une bibliothèque de prérequis importante nommée mpmath. Il s'agit d'une bibliothèque Python pour l'arithmétique à virgule flottante réelle et complexe avec une précision arbitraire. Cependant, le programme d'installation de package de Python PIP l'installe automatiquement lorsque SymPy est installé comme suit -
pip install sympyD'autres distributions Python telles que Anaconda, Enthought Canopy, etc., peuvent avoir SymPy déjà intégré. Pour vérifier, vous pouvez taper ce qui suit dans l'invite Python -
>>> import sympy
>>> sympy.__version__Et vous obtenez la sortie ci-dessous comme la version actuelle de sympy -
'1.5.1'
Le code source du package SymPy est disponible sur https://github.com/sympy/sympy.
Le calcul symbolique fait référence au développement d'algorithmes pour manipuler des expressions mathématiques et d'autres objets mathématiques. Le calcul symbolique intègre les mathématiques à l'informatique pour résoudre des expressions mathématiques à l'aide de symboles mathématiques. Un système d'algèbre informatique (CAS) tel que SymPy évalue les expressions algébriques exactement (pas approximativement) en utilisant les mêmes symboles que ceux utilisés dans la méthode manuelle traditionnelle. Par exemple, nous calculons la racine carrée d'un nombre en utilisant le module mathématique de Python comme indiqué ci-dessous -
>>> import math
>>> print (math.sqrt(25), math.sqrt(7))La sortie de l'extrait de code ci-dessus est la suivante -
5.0 2.6457513110645907
Comme vous pouvez le voir, la racine carrée de 7 est calculée approximativement. Mais dans SymPy, les racines carrées de nombres qui ne sont pas des carrés parfaits ne sont pas évaluées par défaut, comme indiqué ci-dessous -
>>> import sympy
>>> print (sympy.sqrt(7))La sortie de l'extrait de code ci-dessus est la suivante -
sqrt(7)
Il est possible de simplifier et d'afficher le résultat de l'expression symboliquement avec l'extrait de code ci-dessous -
>>> import math
>>> print (math.sqrt(12))La sortie de l'extrait de code ci-dessus est la suivante -
3.4641016151377544
Vous devez utiliser l'extrait de code ci-dessous pour exécuter la même chose en utilisant sympy -
##sympy output
>>> print (sympy.sqrt(12))Et la sortie pour cela est la suivante -
2*sqrt(3)
Le code SymPy, lorsqu'il est exécuté dans le bloc-notes Jupyter, utilise la bibliothèque MathJax pour restituer des symboles mathématiques sous forme LatEx. Il est montré dans l'extrait de code ci-dessous -
>>> from sympy import *
>>> x=Symbol ('x')
>>> expr = integrate(x**x, x)
>>> exprLors de l'exécution de la commande ci-dessus dans le shell python, la sortie suivante sera générée -
Integral(x**x, x)Ce qui équivaut à
$\int \mathrm{x}^{x}\,\mathrm{d}x$
La racine carrée d'un carré non parfait peut être représentée par Latex comme suit en utilisant le symbole traditionnel -
>>> from sympy import *
>>> x=7
>>> sqrt(x)La sortie de l'extrait de code ci-dessus est la suivante -
$\sqrt7$
Un système de calcul symbolique tel que SymPy effectue toutes sortes de calculs (tels que des dérivés, des intégrales et des limites, résoudre des équations, travailler avec des matrices) symboliquement. Le package SymPy contient différents modules prenant en charge le traçage, l'impression (comme LATEX), la physique, les statistiques, la combinatoire, la théorie des nombres, la géométrie, la logique, etc.
Le module principal du package SymPy contient la classe Number qui représente les nombres atomiques. Cette classe a deux sous-classes: Float et Rational class. La classe rationnelle est encore étendue par la classe Integer.
La classe Float représente un nombre à virgule flottante de précision arbitraire.
>>> from sympy import Float
>>> Float(6.32)La sortie de l'extrait de code ci-dessus est la suivante -
6.32
SymPy peut convertir un entier ou une chaîne en float.
>>> Float(10)10.0
Float('1.33E5')# scientific notation133000.0
Lors de la conversion en float, il est également possible de spécifier le nombre de chiffres pour la précision comme indiqué ci-dessous -
>>> Float(1.33333,2)La sortie de l'extrait de code ci-dessus est la suivante -
1.3
Une représentation d'un nombre (p / q) est représentée en tant qu'objet de classe rationnelle avec q étant un nombre non nul.
>>> Rational(3/4)La sortie de l'extrait de code ci-dessus est la suivante -
$\frac{3}{4}$
Si un nombre à virgule flottante est passé au constructeur Rational (), il renvoie la valeur sous-jacente de sa représentation binaire
>>> Rational(0.2)La sortie de l'extrait de code ci-dessus est la suivante -
$\frac{3602879701896397}{18014398509481984}$
Pour une représentation plus simple, spécifiez la limitation du dénominateur.
>>> Rational(0.2).limit_denominator(100)La sortie de l'extrait de code ci-dessus est la suivante -
$\frac{1}{5}$
Lorsqu'une chaîne est passée au constructeur Rational (), un nombre rationnel de précision arbitraire est renvoyé.
>>> Rational("3.65")La sortie de l'extrait de code ci-dessus est la suivante -
$\frac{73}{20}$
L'objet rationnel peut également être obtenu si deux arguments numériques sont passés. Les parties numérateur et dénominateur sont disponibles en tant que propriétés.
>>> a=Rational(3,5)
>>> print (a)
>>> print ("numerator:{}, denominator:{}".format(a.p, a.q))La sortie de l'extrait de code ci-dessus est la suivante -
3/5
numerator:3, denominator:5
>>> aLa sortie de l'extrait de code ci-dessus est la suivante -
$\frac{3}{5}$
La classe Integer dans SymPy représente un nombre entier de n'importe quelle taille. Le constructeur peut accepter un nombre flottant ou rationnel, mais la partie fractionnaire est rejetée
>>> Integer(10)La sortie de l'extrait de code ci-dessus est la suivante -
10
>>> Integer(3.4)La sortie de l'extrait de code ci-dessus est la suivante -
3
>>> Integer(2/7)La sortie de l'extrait de code ci-dessus est la suivante -
0
SymPy a un RealNumberclasse qui agit comme alias pour Float. SymPy définit également Zero et One comme des classes singleton accessibles avec S.Zero et S.One respectivement comme indiqué ci-dessous -
>>> S.ZeroLa sortie est la suivante -
0
>>> S.OneLa sortie est la suivante -
1
Les autres objets numériques Singleton prédéfinis sont Half, NaN, Infinity et ImaginaryUnit
>>> from sympy import S
>>> print (S.Half)La sortie est la suivante -
½
>>> print (S.NaN)La sortie est la suivante -
nan
Infinity est disponible en tant qu'objet symbole oo ou S.Infinity
>>> from sympy import oo
>>> ooLa sortie de l'extrait de code ci-dessus est la suivante -
$\infty$
>>> S.InfinityLa sortie de l'extrait de code ci-dessus est la suivante -
$\infty$
Le numéro ImaginaryUnit peut être importé en tant que symbole I ou accessible en tant que S.ImaginaryUnit et représente la racine carrée de -1
>>> from sympy import I
>>> ILorsque vous exécutez l'extrait de code ci-dessus, vous obtenez la sortie suivante -
i
>>> S.ImaginaryUnitLa sortie de l'extrait de code ci-dessus est la suivante -
i
>>> from sympy import sqrt
>>> i=sqrt(-1)
>>> i*iLorsque vous exécutez l'extrait de code ci-dessus, vous obtenez la sortie suivante -
-1
Symbolest la classe la plus importante de la bibliothèque symPy. Comme mentionné précédemment, les calculs symboliques sont effectués avec des symboles. Les variables SymPy sont des objets de la classe Symbols.
L'argument de la fonction Symbol () est une chaîne contenant un symbole qui peut être affecté à une variable.
>>> from sympy import Symbol
>>> x=Symbol('x')
>>> y=Symbol('y')
>>> expr=x**2+y**2
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x^2 + y^2$
Un symbole peut être composé de plusieurs alphabets.
>>> s=Symbol('side')
>>> s**3L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$side^3$
SymPy dispose également d'un Symbols()fonction qui peut définir plusieurs symboles à la fois. La chaîne contient des noms de variables séparés par une virgule ou un espace.
>>> from sympy import symbols
>>> x,y,z=symbols("x,y,z")Dans le module abc de SymPy, tous les alphabets latins et grecs sont définis comme des symboles. Par conséquent, au lieu d'instancier l'objet Symbol, cette méthode est pratique.
>>> from sympy.abc import x,y,zCependant, les noms C, O, S, I, N, E et Qsont des symboles prédéfinis. De plus, les symboles avec plus d'un alphabets ne sont pas définis dans le module abc, pour lequel vous devez utiliser l'objet Symbol comme ci-dessus. Le module abc définit des noms spéciaux qui peuvent détecter des définitions dans l'espace de noms SymPy par défaut. clash1 contient des lettres simples et clash2 a des symboles de conflit de plusieurs lettres
>>> from sympy.abc import _clash1, _clash2
>>> _clash1La sortie de l'extrait de code ci-dessus est la suivante -
{'C': C, 'O': O, 'Q': Q, 'N': N, 'I': I, 'E': E, 'S': S}
>>> _clash2La sortie de l'extrait de code ci-dessus est la suivante -
{'beta': beta, 'zeta': zeta, 'gamma': gamma, 'pi': pi}
Les symboles indexés peuvent être définis à l'aide d'une syntaxe similaire à la fonction range (). Les plages sont indiquées par un deux-points. Le type de plage est déterminé par le caractère à droite des deux points. Si itr est un chiffre, tous les chiffres contigus à gauche sont pris comme valeur de départ non négative. Tous les chiffres contigus à droite sont considérés comme 1 supérieur à la valeur de fin.
>>> from sympy import symbols
>>> symbols('a:5')La sortie de l'extrait de code ci-dessus est la suivante -
(a0, a1, a2, a3, a4)
>>> symbols('mark(1:4)')La sortie de l'extrait de code ci-dessus est la suivante -
(mark1, mark2, mark3)
L'une des opérations les plus élémentaires à effectuer sur une expression mathématique est la substitution. La fonction subs () de SymPy remplace toutes les occurrences du premier paramètre par le second.
>>> from sympy.abc import x,a
>>> expr=sin(x)*sin(x)+cos(x)*cos(x)
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\sin^2(x)+\cos^2(x)$
>>> expr.subs(x,a)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\sin^2(a)+\cos^2(a)$
Cette fonction est utile si nous voulons évaluer une certaine expression. Par exemple, nous voulons calculer les valeurs de l'expression suivante en remplaçant a par 5.
>>> expr=a*a+2*a+5
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$a^2 + 2a + 5$
expr.subs(a,5)L'extrait de code ci-dessus donne la sortie suivante -
40
>>> from sympy.abc import x
>>> from sympy import sin, pi
>>> expr=sin(x)
>>> expr1=expr.subs(x,pi)
>>> expr1L'extrait de code ci-dessus donne la sortie suivante -
0
Cette fonction est également utilisée pour remplacer une sous-expression par une autre sous-expression. Dans l'exemple suivant, b est remplacé par a + b.
>>> from sympy.abc import a,b
>>> expr=(a+b)**2
>>> expr1=expr.subs(b,a+b)
>>> expr1L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$(2a + b)^2$
La fonction sympify () est utilisée pour convertir toute expression arbitraire afin qu'elle puisse être utilisée comme une expression SymPy. Les objets Python normaux tels que les objets entiers sont convertis dans SymPy. Entiers, etc., les chaînes sont également converties en expressions SymPy.
>>> expr="x**2+3*x+2"
>>> expr1=sympify(expr)
>>> expr1
>>> expr1.subs(x,2)L'extrait de code ci-dessus donne la sortie suivante -
12
Tout objet Python peut être converti en objet SymPy. Cependant, puisque la conversion utilise en interne la fonction eval (), l'expression non assainie ne doit pas être utilisée, sinon SympifyError est levée.
>>> sympify("x***2")
---------------------------------------------------------------------------SympifyError: Sympify de l'expression 'n'a pas pu analyser' x *** 2 '' a échoué, car une exception a été déclenchée.
La fonction sympify () prend les arguments suivants: * strict: la valeur par défaut est False. Si la valeur est True, seuls les types pour lesquels une conversion explicite a été définie sont convertis. Sinon, SympifyError est déclenché. * evaluer: Si la valeur est False, l'arithmétique et les opérateurs seront convertis en leurs équivalents SymPy sans évaluer l'expression.
>>> sympify("10/5+4/2")L'extrait de code ci-dessus donne la sortie suivante -
4
>>> sympify("10/5+4/2", evaluate=False)L'extrait de code ci-dessus donne la sortie suivante -
$\frac{10}{5}+\frac{4}{2}$
Cette fonction évalue une expression numérique donnée jusqu'à une précision de virgule flottante donnée jusqu'à 100 chiffres. La fonction prend également sous le paramètre un objet de dictionnaire de valeurs numériques pour les symboles. Considérez l'expression suivante
>>> from sympy.abc import r
>>> expr=pi*r**2
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\Pi{r^2}$
Pour évaluer l'expression ci-dessus en utilisant la fonction evalf () en remplaçant r par 5
>>> expr.evalf(subs={r:5})L'extrait de code ci-dessus donne la sortie suivante -
78.5398163397448
Par défaut, la précision en virgule flottante comprend jusqu'à 15 chiffres qui peuvent être remplacés par n'importe quel nombre jusqu'à 100. L'expression suivante est évaluée jusqu'à 20 chiffres de précision.
>>> expr=a/b
>>> expr.evalf(20, subs={a:100, b:3})L'extrait de code ci-dessus donne la sortie suivante -
33.333333333333333333
La fonction lambdify traduit les expressions SymPy en fonctions Python. Si une expression doit être évaluée sur une large plage de valeurs, la fonction evalf () n'est pas efficace. lambdify agit comme une fonction lambda, sauf qu'il convertit les noms SymPy en noms de la bibliothèque numérique donnée, généralement NumPy. Par défaut, lambdify sur les implémentations dans la bibliothèque standard math.
>>> expr=1/sin(x)
>>> f=lambdify(x, expr)
>>> f(3.14)L'extrait de code ci-dessus donne la sortie suivante -
627.8831939138764
L'expression peut avoir plusieurs variables. Dans ce cas, le premier argument de la fonction lambdify () est une liste de variables, suivie de l'expression à évaluer.
>>> expr=a**2+b**2
>>> f=lambdify([a,b],expr)
>>> f(2,3)L'extrait de code ci-dessus donne la sortie suivante -
13
Cependant, pour tirer parti de la bibliothèque numpy en tant que backend numérique, nous devons définir la même chose comme argument de la fonction lambdify ().
>>> f=lambdify([a,b],expr, "numpy")Nous utilisons deux tableaux numpy pour deux arguments a et b dans la fonction ci-dessus. Le temps d'exécution est considérablement rapide dans le cas de tableaux numpy.
>>> import numpy
>>> l1=numpy.arange(1,6)
>>> l2=numpy.arange(6,11)
>>> f(l1,l2)L'extrait de code ci-dessus donne la sortie suivante -
array([ 37, 53, 73, 97, 125], dtype=int32)
Les fonctions booléennes sont définies dans sympy.basic.booleanarg module. Il est possible de construire des expressions booléennes avec les opérateurs python standard & (Et), | (Ou), ~ (Non) ainsi qu'avec >> et <<. Les expressions booléennes héritent de la classe Basic définie dans le module principal de SymPy.
Fonction BooleanTrue
Cette fonction est équivalente à True comme dans le noyau Python. Il renvoie un singleton qui peut être récupéré par S.true.
>>> from sympy import *
>>> x=sympify(true)
>>> x, S.trueL'extrait de code ci-dessus donne la sortie suivante -
(Vrai vrai)
Fonction BooleanFalse
De même, cette fonction est équivalente à Boolean False en Python et est accessible par S.false
>>> from sympy import *
>>> x=sympify(false)
>>> x, S.falseL'extrait de code ci-dessus donne la sortie suivante -
(Faux, Faux)
Et fonction
Une fonction logique AND évalue ses deux arguments et renvoie False si l'un d'eux est False. La fonction émule l'opérateur &.
>>> from sympy import *
>>> from sympy.logic.boolalg import And
>>> x,y=symbols('x y')
>>> x=True
>>> y=True
>>> And(x,y), x"&"yL'extrait de code ci-dessus donne la sortie suivante -
(Vrai vrai)
>>> y=False
>>> And(x,y), x"&"yL'extrait de code ci-dessus donne la sortie suivante -
(Faux, Faux)
Ou fonction
Cette fonction évalue deux arguments booléens et renvoie True si l'un d'eux est True. Le | L'opérateur émule son comportement.
>>> from sympy import *
>>> from sympy.logic.boolalg import Or
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Or(x,y), x|yL'extrait de code ci-dessus donne la sortie suivante -
(Vrai vrai)
>>> x=False
>>> y=False
>>> Or(x,y), x|yL'extrait de code ci-dessus donne la sortie suivante -
(Faux, Faux)
Pas de fonction
Une fonction Logical Not entraîne la négation de l'argument booléen. Il renvoie True si son argument est False et renvoie False si True. L'opérateur ~ exécute l'opération similaire à la fonction Not. Il est montré dans l'exemple ci-dessous -
>>> from sympy import *
>>> from sympy.logic.boolalg import Or, And, Not
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Not(x), Not(y)L'extrait de code ci-dessus donne la sortie suivante -
(Faux vrai)
>>> Not(And(x,y)), Not(Or(x,y))L'extrait de code ci-dessus donne la sortie suivante -
(Vrai faux)
Fonction Xor
La fonction XOR logique (OU exclusif) renvoie True si un nombre impair d'arguments est True et le reste est False et renvoie False si un nombre pair d'arguments est True et le reste est False. Une opération similaire est effectuée par l'opérateur ^.
>>> from sympy import *
>>> from sympy.logic.boolalg import Xor
>>> x,y=symbols('x y')
>>> x=True
>>> y=False
>>> Xor(x,y), x^yL'extrait de code ci-dessus donne la sortie suivante -
(Vrai vrai)
>>> a,b,c,d,e=symbols('a b c d e')
>>> a,b,c,d,e=(True, False, True, True, False)
>>> Xor(a,b,c,d,e)L'extrait de code ci-dessus donne la sortie suivante -
Vrai
Dans le cas ci-dessus, trois arguments (nombre impair) sont True, donc Xor retourne vrai. Cependant, si le nombre d'arguments True est pair, il en résulte False, comme indiqué ci-dessous -
>>> a,b,c,d,e=(True, False, False, True, False)
>>> Xor(a,b,c,d,e)L'extrait de code ci-dessus donne la sortie suivante -
Faux
Fonction Nand
Cette fonction effectue une opération logique NAND. Il évalue ses arguments et renvoie True si l'un d'entre eux est False et False s'ils sont tous True.
>>> from sympy import *
>>> from sympy.logic.boolalg import Nand
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Nand(a,b,c), Nand(a,c)L'extrait de code ci-dessus donne la sortie suivante -
(Vrai faux)
Ni fonction
Cette fonction exécute une opération logique NOR. Il évalue ses arguments et renvoie False si l'un d'entre eux est True et True s'ils sont tous False.
>>> from sympy import *
>>> from sympy.logic.boolalg import Nor
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Nor(a,b,c), Nor(a,c)L'extrait de code ci-dessus donne la sortie suivante -
(Faux, Faux)
Notez que même si SymPy fournit l'opérateur ^ pour Xor, ~ pour Not, | pour les fonctions Or et & pour Et par commodité, leur utilisation normale en Python est en tant qu'opérateurs au niveau du bit. Par conséquent, si les opérandes sont des entiers, les résultats seraient différents.
Fonction équivalente
Cette fonction renvoie une relation d'équivalence. Equivalent (A, B) est True si et seulement si A et B sont tous les deux True ou tous les deux False. La fonction renvoie True si tous les arguments sont logiquement équivalents. Renvoie False dans le cas contraire.
>>> from sympy import *
>>> from sympy.logic.boolalg import Equivalent
>>> a,b,c=symbols('a b c')
>>> a,b,c=(True, False, True)
>>> Equivalent(a,b), Equivalent(a,c)L'extrait de code ci-dessus donne la sortie suivante -
(Faux vrai)
Fonction ITE
Cette fonction agit comme la clause If then else dans un langage de programmation.ITE (A, B, C) évalue et renvoie le résultat de B si A est vrai sinon il renvoie le résultat de C. Tous les arguments doivent être des booléens.
>>> from sympy import * >>> from sympy.logic.boolalg import ITE >>> a,b,c=symbols('a b c') >>> a,b,c=(True, False, True)
>>> ITE(a,b,c), ITE(a,c,b)L'extrait de code ci-dessus donne la sortie suivante -
(Faux vrai)
Le module d'hypothèses du package SymPy contient des outils pour extraire des informations sur les expressions. Le module définit la fonction ask () à cet effet.
sympy.assumptions.ask(property)Les propriétés suivantes fournissent des informations utiles sur une expression -
algebraic(x)
Pour être algébrique, un nombre doit être la racine d'une équation polynomiale non nulle à coefficients rationnels. √2 parce que √2 est une solution de x2 - 2 = 0, donc c'est algébrique.
complex(x)
Prédicat de nombre complexe. C'est vrai si et seulement si x appartient à l'ensemble des nombres complexes.
composite(x)
Le prédicat de nombre composé retourné par ask (Q.composite (x)) est vrai si et seulement si x est un entier positif et a au moins un diviseur positif autre que 1 et le nombre lui-même.
even, odd
Le ask () renvoie vrai de x est dans l'ensemble des nombres pairs et l'ensemble des nombres impairs respectivement.
imaginary
Cette propriété représente un prédicat numérique imaginaire. C'est vrai si x peut être écrit comme un nombre réel multiplié par l'unité imaginaire I.
integer
Cette propriété retournée par Q.integer (x) renvoie true si x appartient à un ensemble de nombres pairs.
rational, irrational
Q.irrational (x) est vrai si et seulement si x est un nombre réel qui ne peut pas être exprimé sous forme de rapport d'entiers. Par exemple, pi est un nombre irrationnel.
positive, negative
Prédicats pour vérifier si le nombre est positif ou négatif
zero, nonzero
Prédicats pour vérifier si un nombre est zéro ou non
>>> from sympy import *
>>> x=Symbol('x')
>>> x=10
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask( Q.complex(100))
(True, True)
>>> x,y=symbols("x y")
>>> x,y=5,10
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(False, True)
>>> x,y= 2*I, 4+5*I
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> x,y=5,10
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(False, True, True, False)
>>> x,y=5,-5
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True, True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)Sympy a une puissante capacité à simplifier les expressions mathématiques. Il existe de nombreuses fonctions dans SymPy pour effectuer différents types de simplification. Une fonction générale appelée simplify () est là qui tente d'arriver à la forme la plus simple d'une expression.
simplifier
Cette fonction est définie dans le module sympy.simplify. simplify () essaie d'appliquer des heuristiques intelligentes pour rendre l'expression d'entrée «plus simple». Le code suivant montre simplifie l'expression$sin^2(x)+cos^2(x)$.
>>> from sympy import *
>>> x=Symbol('x')
>>> expr=sin(x)**2 + cos(x)**2
>>> simplify(expr)L'extrait de code ci-dessus donne la sortie suivante -
1
développer
Expand () est l'une des fonctions de simplification les plus courantes de SymPy, utilisée pour développer des expressions polynomiales. Par exemple -
>>> a,b=symbols('a b')
>>> expand((a+b)**2)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$a^2 + 2ab + b^2$
>>> expand((a+b)*(a-b))L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$a^2 - b^2$
La fonction expand () rend les expressions plus grandes, pas plus petites. C'est généralement le cas, mais souvent une expression devient plus petite en appelant expand () dessus.
>>> expand((x + 1)*(x - 2) - (x - 1)*x)L'extrait de code ci-dessus donne la sortie suivante -
-2
facteur
Cette fonction prend un polynôme et le factorise en facteurs irréductibles sur les nombres rationnels.
>>> x,y,z=symbols('x y z')
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor(expr)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$z(x + 2y)^2$
>>> factor(x**2+2*x+1)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$(x + 1)^2$
La fonction factor () est l'opposé de expand (). Chacun des facteurs renvoyés par factor () est garanti irréductible. La fonction factor_list () renvoie une sortie plus structurée.
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z)
>>> factor_list(expr)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
(1, [(z, 1), (x + 2*y, 2)])
collecte
Cette fonction recueille des termes supplémentaires d'une expression par rapport à une liste d'expressions allant jusqu'à des puissances avec des exposants rationnels.
>>> expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x^3 + x^2z + 2x^2 + xy + x - 3$
La fonction collect () sur cette expression résulte comme suit -
>>> collect(expr,x)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x^3 + x^2(2 - z) + x(y + 1) - 3$
>>> expr=y**2*x + 4*x*y*z + 4*y**2*z+y**3+2*x*y
>>> collect(expr,y)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$Y^3+Y^2(x+4z)+y(4xz+2x)$
Annuler
La fonction cancel () prendra n'importe quelle fonction rationnelle et la mettra dans la forme canonique standard, p / q, où p et q sont des polynômes développés sans facteurs communs. Les principaux coefficients de p et q n'ont pas de dénominateurs, c'est-à-dire qu'ils sont des entiers.
>>> expr1=x**2+2*x+1
>>> expr2=x+1
>>> cancel(expr1/expr2)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x+1$
>>> expr = 1/x + (3*x/2 - 2)/(x - 4)
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{\frac{3x}{2} - 2}{x - 4} + \frac{1}{x}$
>>> cancel(expr)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{3x^2 - 2x - 8}{2x^2 - 8}$
>>> expr=1/sin(x)**2
>>> expr1=sin(x)
>>> cancel(expr1*expr)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{1}{\sin(x)}$
trigsimp
Cette fonction est utilisée pour simplifier les identités trigonométriques. On peut noter que les conventions de dénomination des fonctions trigonométriques inverses consistent à ajouter un a au début du nom de la fonction. Par exemple, le cosinus inverse, ou arc cosinus, est appelé acos ().
>>> from sympy import trigsimp, sin, cos
>>> from sympy.abc import x, y
>>> expr = 2*sin(x)**2 + 2*cos(x)**2
>>> trigsimp(expr)2
La fonction trigsimp utilise l'heuristique pour appliquer la meilleure identité trigonométrique appropriée.
powerimp
Cette fonction réduit l'expression donnée en combinant des puissances avec des bases et des exposants similaires.
>>> expr=x**y*x**z*y**z
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x^y x^z y^z$
>>> powsimp(expr)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x^{y+z} y^z$
Vous pouvez faire en sorte que powsimp () ne combine que des bases ou combine uniquement des exposants en changeant combine = 'base' ou combine = 'exp'. Par défaut, combine = 'all', qui fait les deux. Si force est Vrai, alors les bases seront combinées sans vérifier les hypothèses.
>>> powsimp(expr, combine='base', force=True)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x^y(xy)^z$
combsimp
Les expressions combinatoires impliquant des binômes factoriels et peuvent être simplifiées en utilisant la fonction combsimp (). SymPy fournit une fonction factorielle ()
>>> expr=factorial(x)/factorial(x - 3)
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{x!}{(x - 3)!}$
Pour simplifier l'expression combinatoire ci-dessus, nous utilisons la fonction combsimp () comme suit -
>>> combsimp(expr)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x(x-2)(x-1)$
Le binôme (x, y) est le nombre de façons de choisir y éléments parmi un ensemble de x éléments distincts. Il est également souvent écrit sous la forme xCy.
>>> binomial(x,y)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$(\frac{x}{y})$
>>> combsimp(binomial(x+1, y+1)/binomial(x, y))L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{x + 1}{y + 1}$
logcombine
Cette fonction prend des logarithmes et les combine en utilisant les règles suivantes -
- log (x) + log (y) == log (x * y) si les deux sont positifs
- a * log (x) == log (x ** a) si x est positif et a est réel
>>> logcombine(a*log(x) + log(y) - log(z))L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$a\log(x) + \log(y) - \log(z)$
Si le paramètre de force de cette fonction est défini sur Vrai, les hypothèses ci-dessus seront considérées comme valables s'il n'y a pas d'hypothèse déjà en place sur une quantité.
>>> logcombine(a*log(x) + log(y) - log(z), force=True)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\log\frac{x^a y}{z}$
La dérivée d'une fonction est son taux de changement instantané par rapport à l'une de ses variables. Cela équivaut à trouver la pente de la ligne tangente à la fonction en un point. On peut trouver la différenciation des expressions mathématiques sous forme de variables en utilisant la fonction diff () dans le package SymPy.
diff(expr, variable)
>>> from sympy import diff, sin, exp
>>> from sympy.abc import x,y
>>> expr=x*sin(x*x)+1 >>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x\sin(x^2) + 1$
>>> diff(expr,x)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$2x^2\cos(x^2) + \sin(x^2)$
>>> diff(exp(x**2),x)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
2xex2
Pour prendre plusieurs dérivées, passez la variable autant de fois que vous souhaitez la différencier, ou passez un nombre après la variable.
>>> diff(x**4,x,3)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$24x$
>>> for i in range(1,4): print (diff(x**4,x,i))L'extrait de code ci-dessus donne l'expression ci-dessous -
4*x**3
12*x**2
24*x
Il est également possible d'appeler la méthode diff () d'une expression. Cela fonctionne de la même manière que la fonction diff ().
>>> expr=x*sin(x*x)+1
>>> expr.diff(x)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$2x^2\cos(x^2) + \sin(x^2)$
Un dérivé non évalué est créé à l'aide de la classe Derivative. Il a la même syntaxe que la fonction diff (). Pour évaluer un dérivé non évalué, utilisez la méthode doit.
>>> from sympy import Derivative
>>> d=Derivative(expr)
>>> dL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{d}{dx}(x\sin(x^2)+1)$
>>> d.doit()L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$2x^2\cos(x^2) + \sin(x^2)$
Le package SymPy contient le module intégrales. Il implémente des méthodes pour calculer des intégrales définies et indéfinies d'expressions. La méthode integr () est utilisée pour calculer des intégrales définies et indéfinies. Pour calculer une intégrale indéfinie ou primitive, passez simplement la variable après l'expression.
Par exemple -
integrate(f, x)Pour calculer une intégrale définie, passez l'argument comme suit -
(integration_variable, lower_limit, upper_limit)>>> from sympy import *
>>> x,y = symbols('x y')
>>> expr=x**2 + x + 1
>>> integrate(expr, x)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{x^3}{3} + \frac{x^2}{2} + x$
>>> expr=sin(x)*tan(x)
>>> expr
>>> integrate(expr,x)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$-\frac{\log(\sin(x) - 1)}{2} + \frac{\log(\sin(x) + 1)}{2} - \sin(x)$
L'exemple d'intégrale définie est donné ci-dessous -
>>> expr=exp(-x**2)
>>> integrate(expr,(x,0,oo) )L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{\sqrt\pi}{2}$
Vous pouvez passer plusieurs tuples de limite pour effectuer une intégrale multiple. Un exemple est donné ci-dessous -
>>> expr=exp(-x**2 - y**2)
>>> integrate(expr,(x,0,oo),(y,0,oo))L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{\pi}{4}$
Vous pouvez créer une intégrale non évaluée à l'aide de l'objet Integral, qui peut être évalué en appelant la méthode doit ().
>>> expr = Integral(log(x)**2, x)
>>> exprL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\int \mathrm\log(x)^2 \mathrm{d}x$
>>> expr.doit()L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x\log(x)^2 - 2xlog(x) + 2x$
Transformations intégrales
SymPy prend en charge divers types de transformations intégrales comme suit -
- laplace_transform
- fourier_transform
- sine_transform
- cosine_transform
- hankel_transform
Ces fonctions sont définies dans le module sympy.integrals.transforms. Les exemples suivants calculent respectivement la transformée de Fourier et la transformée de Laplace.
Example 1
>>> from sympy import fourier_transform, exp
>>> from sympy.abc import x, k
>>> expr=exp(-x**2)
>>> fourier_transform(expr, x, k)Lors de l'exécution de la commande ci-dessus dans le shell python, la sortie suivante sera générée -
sqrt(pi)*exp(-pi**2*k**2)Ce qui équivaut à -
$\sqrt\pi * e^{\pi^2k^2}$
Example 2
>>> from sympy.integrals import laplace_transform
>>> from sympy.abc import t, s, a
>>> laplace_transform(t**a, t, s)Lors de l'exécution de la commande ci-dessus dans le shell python, la sortie suivante sera générée -
(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)En mathématiques, une matrice est un tableau à deux dimensions de nombres, de symboles ou d'expressions. La théorie de la manipulation matricielle traite de l'exécution d'opérations arithmétiques sur des objets matriciels, sous réserve de certaines règles.
La transformation linéaire est l'une des applications importantes des matrices. De nombreux domaines scientifiques, spécialement liés à la physique, utilisent des applications liées à la matrice.
Le package SymPy a un module matrices qui traite de la gestion des matrices. Il inclut la classe Matrix dont l'objet représente une matrice.
Note: If you want to execute all the snippets in this chapter individually, you need to import the matrix module as shown below −
>>> from sympy.matrices import MatrixExample
>>> from sympy.matrices import Matrix
>>> m=Matrix([[1,2,3],[2,3,1]])
>>> m
$\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 3 & 1\end{matrix}\right]$Lors de l'exécution de la commande ci-dessus dans le shell python, la sortie suivante sera générée -
[1 2 3 2 3 1]
La matrice est créée à partir d'objets List de taille appropriée. Vous pouvez également obtenir une matrice en distribuant les éléments de liste dans un nombre spécifié de lignes et de colonnes.
>>> M=Matrix(2,3,[10,40,30,2,6,9])
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$Lors de l'exécution de la commande ci-dessus dans le shell python, la sortie suivante sera générée -
[10 40 30 2 6 9]
Matrix est un objet mutable. Le module matrices fournit également la classe ImmutableMatrix pour obtenir une matrice immuable.
Manipulation de base
le shape propriété de l'objet Matrix renvoie sa taille.
>>> M.shapeLa sortie pour le code ci-dessus est la suivante -
(2,3)
Les méthodes row () et col () retournent respectivement la ligne ou la colonne du nombre spécifié.
>>> M.row(0)
$\displaystyle \left[\begin{matrix}10 & 40 & 30\end{matrix}\right]$La sortie pour le code ci-dessus est la suivante -
[10 40 30]
>>> M.col(1)
$\displaystyle \left[\begin{matrix}40\\6\end{matrix}\right]$La sortie pour le code ci-dessus est la suivante -
[40 6]
Utilisez l'opérateur de tranche de Python pour récupérer un ou plusieurs éléments appartenant à une ligne ou une colonne.
>>> M.row(1)[1:3]
[6, 9]La classe Matrix a des méthodes row_del () et col_del () qui suppriment la ligne / colonne spécifiée de la matrice donnée -
>>> M=Matrix(2,3,[10,40,30,2,6,9])
>>> M.col_del(1)
>>> MLors de l'exécution de la commande ci-dessus dans le shell python, la sortie suivante sera générée -
Matrix([[10, 30],[ 2, 9]])Vous pouvez appliquer un style à la sortie à l'aide de la commande suivante -
$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$Vous obtenez la sortie suivante après avoir exécuté l'extrait de code ci-dessus -
[10 30 2 9]
>>> M.row_del(0)
>>> M
$\displaystyle \left[\begin{matrix}2 & 9\end{matrix}\right]$Vous obtenez la sortie suivante après avoir exécuté l'extrait de code ci-dessus -
[2 9]
De même, les méthodes row_insert () et col_insert () ajoutent des lignes ou des colonnes à l'index de ligne ou de colonne spécifié
>>> M1=Matrix([[10,30]])
>>> M=M.row_insert(0,M1)
>>> M
$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$Vous obtenez la sortie suivante après avoir exécuté l'extrait de code ci-dessus -
[10 40 30 2 9]
>>> M2=Matrix([40,6])
>>> M=M.col_insert(1,M2)
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$Vous obtenez la sortie suivante après avoir exécuté l'extrait de code ci-dessus -
[10 40 30 6 9]
Opérations arithmétiques
Les opérateurs habituels +, - et * sont définis pour effectuer l'addition, la soustraction et la multiplication.
>>> M1=Matrix([[1,2,3],[3,2,1]])
>>> M2=Matrix([[4,5,6],[6,5,4]])
>>> M1+M2
$\displaystyle \left[\begin{matrix}5 & 7 & 9\\9 & 7 & 5\end{matrix}\right]$Vous obtenez la sortie suivante après avoir exécuté l'extrait de code ci-dessus -
[5 7 9 9 7 5]
>>> M1-M2
$\displaystyle \left[\begin{matrix}-3 & -3 & -3\\-3 & -3 & -3\end{matrix}\right]$Vous obtenez la sortie suivante après avoir exécuté l'extrait de code ci-dessus -
[- 3 -3 -3 -3 -3 -3]
La multiplication de la matrice n'est possible que si - Le nombre de colonnes de la 1ère matrice doit être égal au nombre de lignes de la 2ème matrice. - Et le résultat aura le même nombre de lignes que la 1ère matrice, et le même nombre de colonnes que la 2ème matrice.
>>> M1=Matrix([[1,2,3],[3,2,1]])
>>> M2=Matrix([[4,5],[6,6],[5,4]])
>>> M1*M2
$\displaystyle \left[\begin{matrix}31 & 29\\29 & 31\end{matrix}\right]$La sortie pour le code ci-dessus est la suivante -
[31 29 29 31]
>>> M1.T
$\displaystyle \left[\begin{matrix}1 & 3\\2 & 2\\3 & 1\end{matrix}\right]$La sortie suivante est obtenue après l'exécution du code -
[1 3 2 2 3 1]
Pour calculer un déterminant de matrice, utilisez la méthode det (). Un déterminant est une valeur scalaire qui peut être calculée à partir des éléments d'une matrice carrée.
>>> M=Matrix(3,3,[10,20,30,5,8,12,9,6,15])
>>> M
$\displaystyle \left[\begin{matrix}10 & 20 & 30\\5 & 8 & 12\\9 & 6 & 15\end{matrix}\right]$La sortie pour le code ci-dessus est la suivante -
[10 20 30 5 8 12 9 6 15]
>>> M.det()La sortie pour le code ci-dessus est la suivante -
-120
Constructeurs de matrices
SymPy fournit de nombreux types spéciaux de classes matricielles. Par exemple, matrice d'identité, matrice de tous les zéros et les uns, etc. Ces classes sont nommées respectivement oeil, zéros et uns. La matrice d'identité est une matrice carrée dont les éléments tombant en diagonale sont mis à 1, le reste des éléments est à 0.
Example
from sympy.matrices import eye eye(3)Output
Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$La sortie pour le code ci-dessus est la suivante -
[1 0 0 0 1 0 0 0 1]
Dans la matrice diag, les éléments en diagonale sont initialisés selon les arguments fournis.
>>> from sympy.matrices import diag
>>> diag(1,2,3)
$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 2 & 0\\0 & 0 & 3\end{matrix}\right]$La sortie pour le code ci-dessus est la suivante -
[1 0 0 0 2 0 0 0 3]
Tous les éléments de la matrice des zéros sont initialisés à 0.
>>> from sympy.matrices import zeros
>>> zeros(2,3)
$\displaystyle \left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]$La sortie pour le code ci-dessus est la suivante -
[0 0 0 0 0 0]
De même, uns est une matrice avec tous les éléments mis à 1.
>>> from sympy.matrices import ones
>>> ones(2,3)
$\displaystyle \left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]$La sortie pour le code ci-dessus est la suivante -
[1 1 1 1 1 1]
Le package Sympy a la classe Function, qui est définie dans le module sympy.core.function. Il s'agit d'une classe de base pour toutes les fonctions mathématiques appliquées, ainsi que d'un constructeur pour les classes de fonctions non définies.
Les catégories de fonctions suivantes sont héritées de la classe Function -
- Fonctions pour nombre complexe
- Fonctions trigonométriques
- Fonctions pour nombre entier
- Fonctions combinatoires
- Autres fonctions diverses
Fonctions pour nombre complexe
Cet ensemble de fonctions est défini dans sympy.functions.elementary.complexes module.
re
Cette fonction renvoie une partie réelle d'une expression -
>>> from sympy import *
>>> re(5+3*I)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
5
>>> re(I)La sortie de l'extrait de code ci-dessus est -
0
Im
Cette fonction renvoie une partie imaginaire d'une expression -
>>> im(5+3*I)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
3
>>> im(I)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
1
sign
Cette fonction renvoie le signe complexe d'une expression.
Pour une expression réelle, le signe sera -
- 1 si l'expression est positive
- 0 si l'expression est égale à zéro
- -1 si l'expression est négative
Si l'expression est imaginaire, le signe renvoyé est -
- I si im (expression) est positive
- -I si im (expression) est négatif
>>> sign(1.55), sign(-1), sign(S.Zero)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
(1, -1, 0)
>>> sign (-3*I), sign(I*2)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
(-I, I)
Abs
Cette fonction renvoie la valeur absolue d'un nombre complexe. Elle est définie comme la distance entre l'origine (0,0) et le point (a, b) dans le plan complexe. Cette fonction est une extension de la fonction intégrée abs () pour accepter des valeurs symboliques.
>>> Abs(2+3*I)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
$\sqrt13$
conjugate
Cette fonction renvoie le conjugué d'un nombre complexe. Pour trouver le conjugué complexe, nous changeons le signe de la partie imaginaire.
>>> conjugate(4+7*I)Vous obtenez la sortie suivante après avoir exécuté l'extrait de code ci-dessus -
4 - 7i
Fonctions trigonométriques
SymPy a des définitions pour tous les rapports trigonométriques - sin cos, tan etc. ainsi que ses équivalents inverses tels que asin, acos, atan etc. Ces fonctions calculent la valeur respective pour un angle donné exprimé en radians.
>>> sin(pi/2), cos(pi/4), tan(pi/6)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
(1, sqrt(2)/2, sqrt(3)/3)
>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
(pi/2, pi/4, pi/6)
Fonctions sur nombre entier
Il s'agit d'un ensemble de fonctions permettant d'effectuer diverses opérations sur un nombre entier.
ceiling
Il s'agit d'une fonction univariée qui renvoie la plus petite valeur entière non inférieure à son argument. En cas de nombres complexes, plafond des parties réelles et imaginaires séparément.
>>> ceiling(pi), ceiling(Rational(20,3)), ceiling(2.6+3.3*I)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
(4, 7, 3 + 4*I)
floor
Cette fonction renvoie la plus grande valeur entière non supérieure à son argument. Dans le cas de nombres complexes, cette fonction prend également la parole des parties réelles et imaginaires séparément.
>>> floor(pi), floor(Rational(100,6)), floor(6.3-5.9*I)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
(3, 16, 6 - 6*I)
frac
Cette fonction représente la partie fractionnaire de x.
>>> frac(3.99), frac(Rational(10,3)), frac(10)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
(0.990000000000000, 1/3, 0)
Fonctions combinatoires
La combinatoire est un domaine des mathématiques concerné par les problèmes de sélection, d'arrangement et de fonctionnement dans un système fini ou discret.
factorial
La factorielle est très importante en combinatoire où elle donne le nombre de façons dont n objets peuvent être permutés. Il est symboliquement représenté par ð ?? '¥! Cette fonction est l'implémentation de la fonction factorielle sur des entiers non négatifs, la factorielle d'un entier négatif est l'infini complexe.
>>> x=Symbol('x')
>>> factorial(x)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
x!
>>> factorial(5)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
120
>>> factorial(-1)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
$\infty\backsim$
binôme
Cette fonction correspond au nombre de façons dont nous pouvons choisir k éléments parmi un ensemble de n éléments.
>>> x,y=symbols('x y')
>>> binomial(x,y)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
$(\frac{x}{y})$
>>> binomial(4,2)La sortie de l'extrait de code ci-dessus est donnée ci-dessous -
6
Les lignes du triangle de Pascal peuvent être générées avec la fonction binomiale.
>>> for i in range(5): print ([binomial(i,j) for j in range(i+1)])Vous obtenez la sortie suivante après avoir exécuté l'extrait de code ci-dessus -
[1]
[1, 1]
[1, 2, 1]
[1, 3, 3, 1]
[1, 4, 6, 4, 1]
fibonacci
Les nombres de Fibonacci sont la séquence entière définie par les termes initiaux F0 = 0, F1 = 1 et la relation de récurrence à deux termes Fn = Fnâˆ'1 + Fnâˆ'2.
>>> [fibonacci(x) for x in range(10)]La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
tribonacci
Les nombres de Tribonacci sont la séquence entière définie par les termes initiaux F0 = 0, F1 = 1, F2 = 1 et la relation de récurrence à trois termes Fn = Fn-1 + Fn-2 + Fn-3.
>>> tribonacci(5, Symbol('x'))L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x^8 + 3x^5 + 3x^2$
>>> [tribonacci(x) for x in range(10)]La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
[0, 1, 1, 2, 4, 7, 13, 24, 44, 81]
Fonctions diverses
Voici une liste de certaines fonctions fréquemment utilisées -
Min- Renvoie la valeur minimale de la liste. Il est nommé Min pour éviter les conflits avec la fonction intégrée min.
Max- Renvoie la valeur maximale de la liste. Il est nommé Max pour éviter les conflits avec la fonction intégrée max.
root - Renvoie la nième racine de x.
sqrt - Renvoie la racine carrée principale de x.
cbrt - Cette fonction calcule la racine cubique principale de x, (raccourci pour x ++ Rational (1,3)).
Voici les exemples des fonctions diverses ci-dessus et de leurs sorties respectives -
>>> Min(pi,E)e
>>> Max(5, Rational(11,2))$\frac{11}{2}$
>>> root(7,Rational(1,2))49
>>> sqrt(2)$\sqrt2$
>>> cbrt(1000)10
En mathématiques, le système de nombres Quaternion est une extension des nombres complexes. Chaque objet Quaternion contient quatre variables scalaires et quatre dimensions, une dimension réelle et trois dimensions imaginaires.
Le quaternion est représenté par l'expression suivante -
q = a + bi + cj + dk
où a, b, c et d sont des nombres réels et i, j, k sont des unités de quaternions telles que, i2 == j2 == k2 == ijk
le sympy.algebras.quaternion module a la classe Quaternion.
>>> from sympy.algebras.quaternion import Quaternion
>>> q=Quaternion(2,3,1,4)
>>> qL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$2 + 3i + 1j + 4k$
Les quaternions sont utilisés en mathématiques pures, ainsi qu'en mathématiques appliquées, infographie, vision par ordinateur, etc.
>>> from sympy import *
>>> x=Symbol('x')
>>> q1=Quaternion(x**2, x**3, x) >>> q1L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$x^2 + x^3i + xj + 0k$
L'objet Quaternion peut également avoir des coefficients imaginaires
>>> q2=Quaternion(2,(3+2*I), x**2, 3.5*I)
>>> q2L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$2 + (3 + 2i)i + x2j + 3.5ik$
ajouter()
Cette méthode disponible dans la classe Quaternion effectue l'ajout de deux objets Quaternion.
>>> q1=Quaternion(1,2,3,4)
>>> q2=Quaternion(4,3,2,1)
>>> q1.add(q2)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$5 + 5i + 5j + 5k$
Il est possible d'ajouter un nombre ou un symbole dans un objet Quaternion.
>>> q1+2La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
$3 + 2i + 3j + 4k$
>>> q1+xLa sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
$(x + 1) + 2i + 3j + 4k$
mul ()
Cette méthode effectue la multiplication de deux objets quaternion.
>>> q1=Quaternion(1,2,1,2)
>>> q2=Quaternion(2,4,3,1)
>>> q1.mul(q2)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$(-11) + 3i + 11j + 7k$
inverse()
Cette méthode renvoie l'inverse d'un objet quaternion.
>>> q1.inverse()L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{1}{10} + (-\frac{1}{5})i + (-\frac{1}{10})j + (-\frac{1}{5})k$
pow ()
Cette méthode renvoie la puissance d'un objet quaternion.
>>> q1.pow(2)La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
$(-8) + 4i + 2j + 4k$
exp ()
Cette méthode calcule l'exponentielle d'un objet Quaternion ie eq
>>> q=Quaternion(1,2,4,3)
>>> q.exp()La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
$e\cos(\sqrt29) + \frac{2\sqrt29e\sin(\sqrt29)}{29}i + \frac{4\sqrt29e\sin(\sqrt29)}{29}j + \frac{3\sqrt29e\sin}{29}k$
Comme les symboles = et == sont définis comme des opérateurs d'affectation et d'égalité en Python, ils ne peuvent pas être utilisés pour formuler des équations symboliques. SymPy fournit la fonction Eq () pour configurer une équation.
>>> from sympy import *
>>> x,y=symbols('x y')
>>> Eq(x,y)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
x = y
Puisque x = y est possible si et seulement si xy = 0, l'équation ci-dessus peut s'écrire -
>>> Eq(x-y,0)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
x − y = 0
Le module solveur de SymPy fournit la fonction soveset () dont le prototype est le suivant -
solveset(equation, variable, domain)Le domaine est par défaut S.Complexes. En utilisant la fonction solveset (), nous pouvons résoudre une équation algébrique comme suit -
>>> solveset(Eq(x**2-9,0), x)La sortie suivante est obtenue -
{−3, 3}
>>> solveset(Eq(x**2-3*x, -2),x)La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
{1,2}
La sortie de Solveset est un FiniteSet des solutions. S'il n'y a pas de solutions, un EmptySet est retourné
>>> solveset(exp(x),x)La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
$\varnothing$
Équation linéaire
Nous devons utiliser la fonction linsolve () pour résoudre des équations linéaires.
Par exemple, les équations sont les suivantes -
xy = 4
x + y = 1
>>> from sympy import *
>>> x,y=symbols('x y')
>>> linsolve([Eq(x-y,4),Eq( x + y ,1) ], (x, y))La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$
La fonction linsolve () peut également résoudre des équations linéaires exprimées sous forme de matrice.
>>> a,b=symbols('a b')
>>> a=Matrix([[1,-1],[1,1]])
>>> b=Matrix([4,1])
>>> linsolve([a,b], (x,y))Nous obtenons la sortie suivante si nous exécutons l'extrait de code ci-dessus -
$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$
Équation non linéaire
Pour cela, nous utilisons la fonction nonlinsolve (). Équations pour cet exemple -
a 2 + a = 0 ab = 0
>>> a,b=symbols('a b')
>>> nonlinsolve([a**2 + a, a - b], [a, b])Nous obtenons la sortie suivante si nous exécutons l'extrait de code ci-dessus -
$\lbrace(-1, -1),(0,0)\rbrace$
équation différentielle
Tout d'abord, créez une fonction non définie en passant cls = Function à la fonction de symboles. Pour résoudre des équations différentielles, utilisez dsolve.
>>> x=Symbol('x')
>>> f=symbols('f', cls=Function)
>>> f(x)La sortie suivante est obtenue après l'exécution de l'extrait de code ci-dessus -
f(x)
Ici f (x) est une fonction non évaluée. Son dérivé est le suivant -
>>> f(x).diff(x)L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$\frac{d}{dx}f(x)$
Nous créons d'abord l'objet Eq correspondant à l'équation différentielle suivante
>>> eqn=Eq(f(x).diff(x)-f(x), sin(x))
>>> eqnL'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$-f(x) + \frac{d}{dx}f(x)= \sin(x)$
>>> dsolve(eqn, f(x))L'extrait de code ci-dessus donne une sortie équivalente à l'expression ci-dessous -
$f(x)=(c^1-\frac{e^-xsin(x)}{2}-\frac{e^-xcos(x)}{2})e^x$
SymPy utilise la bibliothèque Matplotlib comme backend pour rendre les tracés 2D et 3D de fonctions mathématiques. Assurez-vous que Matplotlib est disponible dans l'installation actuelle de Python. Sinon, installez-le en utilisant la commande suivante -
pip install matplotlibLe support de traçage est défini dans le module sympy.plotting. Les fonctions suivantes sont présentes dans le module de traçage -
plot - Tracés linéaires 2D
plot3d - Tracés de lignes 3D
plot_parametric - Graphiques paramétriques 2D
plot3d_parametric - Tracés paramétriques 3D
La fonction plot () renvoie une instance de la classe Plot. Une figure de tracé peut avoir une ou plusieurs expressions SymPy. Bien qu'il soit capable d'utiliser Matplotlib comme backend, d'autres backends tels que texplot, pyglet ou Google charts API peuvent également être utilisés.
plot(expr, range, kwargs)où expr est une expression symPy valide. S'il n'est pas mentionné, la plage utilise la valeur par défaut (-10, 10).
L'exemple suivant trace les valeurs de x2 pour chaque valeur de la plage (-10,10) -
>>> from sympy.plotting import plot
>>> from sympy import *
>>> x=Symbol('x')
>>> plot(x**2, line_color='red')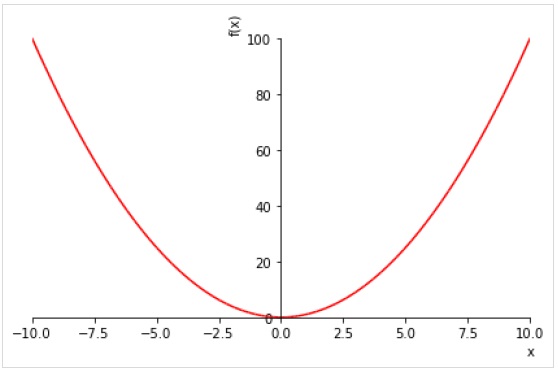
Pour dessiner plusieurs tracés pour la même plage, donnez plusieurs expressions avant le tuple de plage.
>>> plot( sin(x),cos(x), (x, -pi, pi))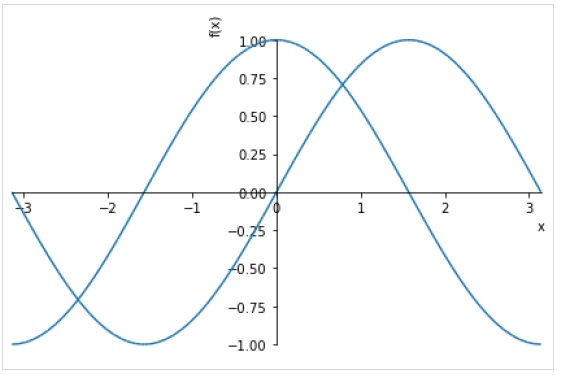
Vous pouvez également spécifier une plage distincte pour chaque expression.
plot((expr1, range1), (expr2, range2))La figure suivante trace sin (x) et cos (x) sur différentes plages.
>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)))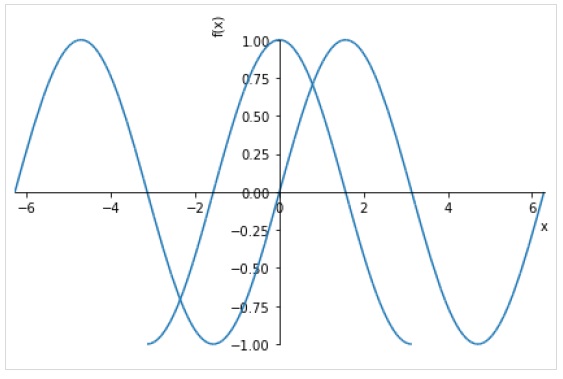
Les arguments de mots-clés facultatifs suivants peuvent être spécifiés dans la fonction plot ().
line_color - spécifie la couleur de la ligne de tracé.
title - une chaîne à afficher comme titre
xlabel - une chaîne à afficher comme étiquette pour l'axe X
ylabel - une chaîne à afficher comme étiquette pour l'axe y
>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)), line_color='red', title='SymPy plot example')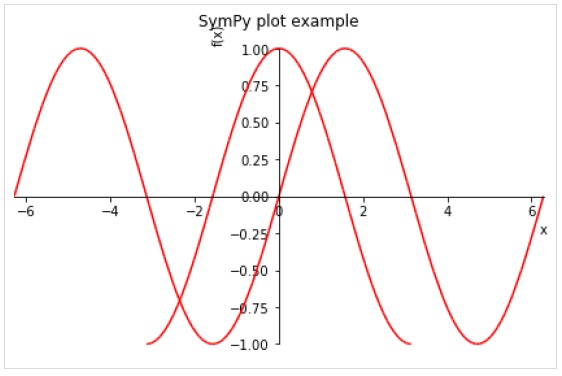
La fonction plot3d () rend un tracé en trois dimensions.
plot3d(expr, xrange, yrange, kwargs)L'exemple suivant dessine un tracé de surface 3D -
>>> from sympy.plotting import plot3d
>>> x,y=symbols('x y')
>>> plot3d(x*y, (x, -10,10), (y, -10,10))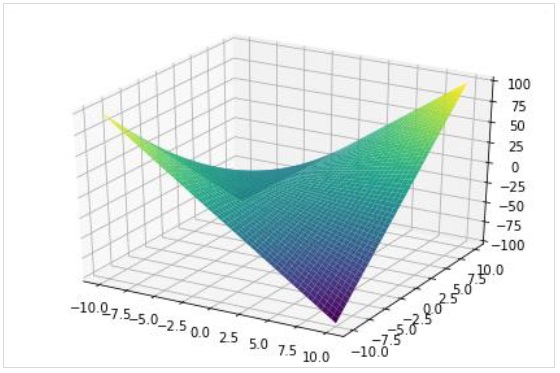
Comme dans le tracé 2D, un tracé tridimensionnel peut également avoir plusieurs tracés, chacun avec une plage différente.
>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))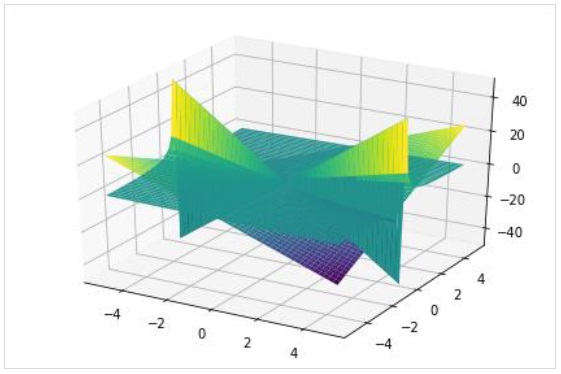
La fonction plot3d_parametric_line () rend un tracé linéaire paramétrique en 3 dimensions.
>>> from sympy.plotting import plot3d_parametric_line
>>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))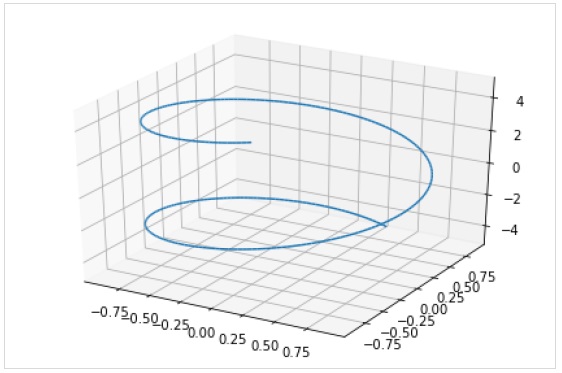
Pour dessiner un tracé de surface paramétrique, utilisez la fonction plot3d_parametric_surface ().
plot3d_parametric_surface(xexpr, yexpr, zexpr, rangex, rangey, kwargs)
>>> from sympy.plotting import plot3d_parametric_surface
>>> plot3d_parametric_surface(cos(x+y), sin(x-y), x-y, (x, -5, 5), (y, -5, 5))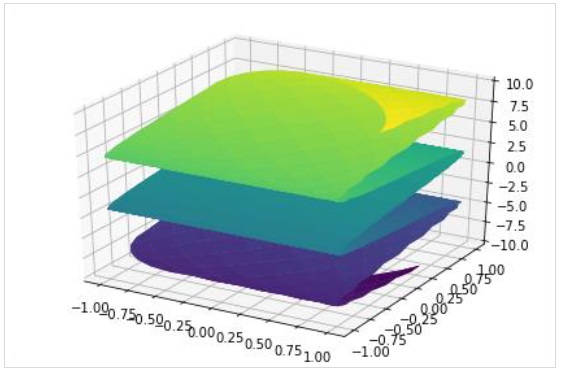
Le module de géométrie de SymPy permet la création d'entités bidimensionnelles telles que la ligne, le cercle, etc. Nous pouvons alors obtenir des informations à leur sujet telles que la vérification de la colinéarité ou la recherche d'intersection.
Point
La classe Point représente un point dans l'espace euclidien. L'exemple suivant vérifie la colinéarité des points -
>>> from sympy.geometry import Point
>>> from sympy import *
>>> x=Point(0,0)
>>> y=Point(2,2)
>>> z=Point(4,4)
>>> Point.is_collinear(x,y,z)Output
True
>>> a=Point(2,3)
>>> Point.is_collinear(x,y,a)Output
False
La méthode distance () de la classe Point calcule la distance entre deux points
>>> x.distance(y)Output
$2\sqrt2$
La distance peut également être représentée en termes de symboles.
Ligne
L'entité de ligne est obtenue à partir de deux objets Point. La méthode intersection () renvoie le point d'intersection si deux lignes se croisent.
>>> from sympy.geometry import Point, Line
>>> p1, p2=Point(0,5), Point(5,0)
>>> l1=Line(p1,p2)
>>> l2=Line(Point(0,0), Point(5,5))
>>> l1.intersection(l2)Output
[Point2D(5/2, 5/2)]
>>> l1.intersection(Line(Point(0,0), Point(2,2)))Output
[Point2D(5/2, 5/2)]
>>> x,y=symbols('x y')
>>> p=Point(x,y)
>>> p.distance(Point(0,0))Output
$\sqrt{x^2 + y^2}$
Triangle
Cette fonction construit une entité triangle à partir de trois objets ponctuels.
Triangle(a,b,c)
>>> t=Triangle(Point(0,0),Point(0,5), Point(5,0))
>>> t.areaOutput
$-\frac{25}{2}$
Ellipse
Une entité de géométrie elliptique est construite en passant un objet Point correspondant au centre et deux nombres chacun pour le rayon horizontal et vertical.
ellipse(center, hradius, vradius)
>>> from sympy.geometry import Ellipse, Line
>>> e=Ellipse(Point(0,0),8,3)
>>> e.areaOutput
$24\pi$
Le vradius peut être fourni indirectement en utilisant le paramètre d'excentricité.
>>> e1=Ellipse(Point(2,2), hradius=5, eccentricity=Rational(3,4))
>>> e1.vradiusOutput
$\frac{5\sqrt7}{4}$
le apoapsis de l'ellipse est la plus grande distance entre le foyer et le contour.
>>> e1.apoapsisOutput
$\frac{35}{4}$
L'instruction suivante calcule la circonférence de l'ellipse -
>>> e1.circumferenceOutput
$20E(\frac{9}{16})$
le equation La méthode de l'ellipse renvoie l'équation de l'ellipse.
>>> e1.equation(x,y)Output
$(\frac{x}{5}-\frac{2}{5})^2 + \frac{16(y-2)2}{175} - 1$
En mathématiques, un ensemble est une collection bien définie d'objets distincts qui peuvent être des nombres, des personnes, des lettres de l'alphabet ou même d'autres ensembles. Set est également l'un des types intégrés à Python. SymPy fournit un module d'ensembles. Il contient des définitions de différents types d'ensemble et a des fonctionnalités pour effectuer des opérations d'ensemble telles que l'intersection, l'union, etc.
Set est une classe de base pour tout autre type d'ensemble dans SymPy. Notez qu'il est différent du type de données d'ensemble intégré de Python. La classe Interval représente des intervalles réels et sa propriété boundary renvoie unFiniteSet objet.
>>> from sympy import Interval
>>> s=Interval(1,10).boundary
>>> type(s)sympy.sets.sets.FiniteSet
FiniteSet est une collection de nombres discrets. Il peut être obtenu à partir de n'importe quel objet de séquence tel qu'une liste ou une chaîne.
>>> from sympy import FiniteSet
>>> FiniteSet(range(5))Output
$\lbrace\lbrace0,1,...,4\rbrace\rbrace$
>>> numbers=[1,3,5,2,8]
>>> FiniteSet(*numbers)Output
$\lbrace1,2,3,5,8\rbrace$
>>> s="HelloWorld"
>>> FiniteSet(*s)Output
{H,W,d,e,l,o,r}
Notez que, comme dans l'ensemble intégré, l'ensemble de SymPy est également une collection d'objets distincts.
ConditionSet est un ensemble d'éléments qui satisfont une condition donnée
>>> from sympy import ConditionSet, Eq, Symbol
>>> x=Symbol('x')
>>> s=ConditionSet(x, Eq(x**2-2*x,0), Interval(1,10)) >>> sOutput
$\lbrace x\mid x\in[1,10]∧x^2 - 2x =0\rbrace$
Unionest un ensemble composé. Il comprend tous les éléments en deux ensembles. Notez que les éléments qui se trouvent dans les deux, n'apparaîtront qu'une seule fois dans l'Union.
>>> from sympy import Union
>>> l1=[3,1,5,7]
>>> l2=[9,7,2,1]
>>> a=FiniteSet(*l1)
>>> b=FiniteSet(*l2)
>>> Union(a,b)Intersection d'autre part, ne contient que les éléments qui sont présents dans les deux.
>>> from sympy import Intersection
>>> Intersection(a,b)ProductSet object représente le produit cartésien des éléments des deux ensembles.
>>> from sympy import ProductSet
>>> l1=[1,2]
>>> l2=[2,3]
>>> a=FiniteSet(*l1)
>>> b=FiniteSet(*l2)
>>> set(ProductSet(a,b))Complement(a,b) conserve les éléments dans a excluant les éléments communs avec l'ensemble b.
>>> from sympy import Complement
>>> l1=[3,1,5,7]
>>> l2=[9,7,2,1]
>>> a=FiniteSet(*l1)
>>> b=FiniteSet(*l2)
>>> Complement(a,b), Complement(b,a)SymmetricDifference set ne contient que des éléments inhabituels dans les deux ensembles.
>>> from sympy import SymmetricDifference
>>> l1=[3,1,5,7]
>>> l2=[9,7,2,1]
>>> a=FiniteSet(*l1)
>>> b=FiniteSet(*l2)
>>> SymmetricDifference(a,b)Output
{2,3,5,9}
Il existe plusieurs imprimantes disponibles dans SymPy. Voici une liste partielle -
- str
- srepr
- Jolie imprimante ASCII
- Jolie imprimante Unicode
- LaTeX
- MathML
- Dot
Les objets SymPy peuvent également être envoyés en sortie vers du code de divers langages, tels que C, Fortran, Javascript, Theano et Python.
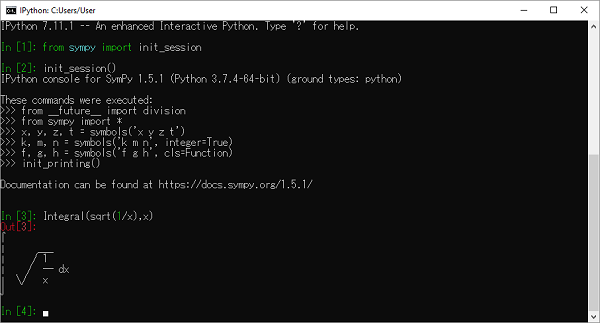
SymPy utilise des caractères Unicode pour rendre la sortie sous la forme d'une jolie impression. Si vous utilisez la console Python pour exécuter une session SymPy, le meilleur environnement d'impression joli est activé en appelant la fonction init_session ().
>>> from sympy import init_session
>>> init_session()Console IPython pour SymPy 1.5.1 (Python 3.7.4-64 bits) (types de masse: python).
Ces commandes ont été exécutées -
>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()La documentation peut être trouvée sur https://docs.sympy.org/1.5.1/.
>>> Integral(sqrt(1/x),x)$\int \sqrt\frac{1}{x} dx$
Si LATEX n'est pas installé, mais que Matplotlib est installé, il utilisera le moteur de rendu Matplotlib. Si Matplotlib n'est pas installé, il utilise la jolie imprimante Unicode. Cependant, le notebook Jupyter utilise MathJax pour rendre LATEX.
Dans un terminal qui ne prend pas en charge Unicode, une jolie imprimante ASCII est utilisée.
Pour utiliser une imprimante ASCII, utilisez la fonction pprint () avec la propriété use_unicode définie sur False
>>> pprint(Integral(sqrt(1/x),x),use_unicode=False)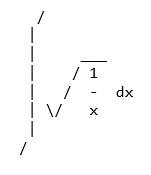
La jolie imprimante Unicode est également accessible depuis pprint () et pretty (). Si le terminal prend en charge Unicode, il est utilisé automatiquement. Si pprint () ne parvient pas à détecter que le terminal prend en charge l'Unicode, vous pouvez passer use_unicode = True pour le forcer à utiliser Unicode.
Pour obtenir la forme LATEX d'une expression, utilisez la fonction latex ().
>>> print(latex(Integral(sqrt(1/x),x)))\int \sqrt{\frac{1}{x}}\, dx
Vous pouvez également utiliser une imprimante mathml. à cet effet, importez la fonction print_mathml. Une version chaîne est obtenue par la fonction mathml ().
>>> from sympy.printing.mathml import print_mathml
>>> print_mathml(Integral(sqrt(1/x),x))<apply>
<int/>
<bvar>
<ci>x</ci>
</bvar>
<apply>
<root/>
<apply>
<power/>
<ci>x</ci>
<cn>-1</cn>
</apply>
</apply>
</apply>
>>>mathml(Integral(sqrt(1/x),x))'<apply><int/><bvar><ci>x</ci></bvar><apply><root/><apply><power/><ci>x</ci><cn>-1</cn></apply></apply></apply>'