ऑप्टिमाइज़ेशन होपफील्ड नेटवर्क का उपयोग करना
अनुकूलन डिजाइन, स्थिति, संसाधन और सिस्टम जैसी किसी चीज़ को यथासंभव प्रभावी बनाने की एक क्रिया है। लागत फ़ंक्शन और ऊर्जा फ़ंक्शन के बीच समानता का उपयोग करके, हम अनुकूलन समस्याओं को हल करने के लिए अत्यधिक परस्पर न्यूरॉन्स का उपयोग कर सकते हैं। इस तरह का तंत्रिका नेटवर्क होपफील्ड नेटवर्क है, जिसमें एक ही परत होती है जिसमें एक या एक से अधिक पूरी तरह से जुड़े हुए न्यूरॉन होते हैं। यह अनुकूलन के लिए इस्तेमाल किया जा सकता है।
अनुकूलन के लिए हॉपफील्ड नेटवर्क का उपयोग करते समय याद रखने वाले बिंदु -
ऊर्जा फ़ंक्शन नेटवर्क का न्यूनतम होना चाहिए।
यह संग्रहीत प्रतिमानों में से किसी एक को चुनने के बजाय संतोषजनक समाधान प्राप्त करेगा।
हॉपफील्ड नेटवर्क द्वारा पाए जाने वाले समाधान की गुणवत्ता नेटवर्क की प्रारंभिक स्थिति पर काफी निर्भर करती है।
ट्रैवलिंग सेल्समैन की समस्या
सेल्समैन द्वारा यात्रा किए गए सबसे छोटे मार्ग का पता लगाना कम्प्यूटेशनल समस्याओं में से एक है, जिसे हॉपफील्ड न्यूरल नेटवर्क का उपयोग करके अनुकूलित किया जा सकता है।
टीएसपी की बुनियादी अवधारणा
ट्रैवलिंग सेल्समैन प्रॉब्लम (TSP) एक क्लासिकल ऑप्टिमाइज़ेशन प्रॉब्लम है जिसमें सेल्समैन को यात्रा करनी पड़ती है nशहर, जो एक दूसरे के साथ जुड़े हुए हैं, लागत को बनाए रखने के साथ-साथ न्यूनतम दूरी तय करते हैं। उदाहरण के लिए, सेल्समैन को 4 शहरों A, B, C, D के सेट की यात्रा करनी होती है और लक्ष्य सबसे छोटा गोलाकार दौरा, ABC-D ढूंढना होता है, ताकि लागत को कम किया जा सके, जिसमें से यात्रा की लागत भी शामिल है पहला शहर ए के आखिरी शहर डी।
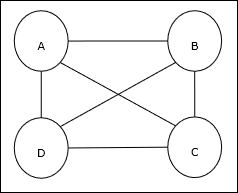
मैट्रिक्स का प्रतिनिधित्व
वास्तव में एन-शहर टीएसपी के प्रत्येक दौरे को व्यक्त किया जा सकता है n × n मैट्रिक्स जिसका ith पंक्ति वर्णन करती है ithशहर का स्थान। यह मैट्रिक्स,M4 शहरों ए, बी, सी, डी के लिए निम्नानुसार व्यक्त किया जा सकता है -
$$ M = \ start {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 & \\ C: & & 0 & 1 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$
हॉपफील्ड नेटवर्क द्वारा समाधान
हॉपफील्ड नेटवर्क द्वारा इस टीएसपी के समाधान पर विचार करते समय, नेटवर्क में प्रत्येक नोड मैट्रिक्स में एक तत्व से मेल खाता है।
ऊर्जा समारोह गणना
अनुकूलित समाधान होने के लिए, ऊर्जा फ़ंक्शन न्यूनतम होना चाहिए। निम्नलिखित बाधाओं के आधार पर, हम निम्न प्रकार से ऊर्जा कार्य की गणना कर सकते हैं -
बाधा-मैं
पहला अवरोध, जिसके आधार पर हम ऊर्जा क्रियाओं की गणना करेंगे, यह है कि मैट्रिक्स की प्रत्येक पंक्ति में एक तत्व 1 के बराबर होना चाहिए M और प्रत्येक पंक्ति में अन्य तत्वों के बराबर होना चाहिए 0क्योंकि प्रत्येक शहर TSP दौरे में केवल एक ही स्थिति में हो सकता है। यह बाधा गणितीय रूप से निम्नानुसार लिखी जा सकती है -
$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: for \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $
अब ऊर्जा को कम करने के लिए, उपरोक्त बाधा के आधार पर, इसमें एक शब्द अनुपात होगा -
$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n \ left (\ start {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {j = 1} ^ n M_ {x, j) } \ अंत {सरणी} \ right) ^ 2 $$
बाधा द्वितीय
जैसा कि हम जानते हैं, टीएसपी में एक शहर मैट्रिक्स के प्रत्येक कॉलम में दौरे में किसी भी स्थिति में हो सकता है M, एक तत्व 1 के बराबर होना चाहिए और अन्य तत्व 0. के बराबर होना चाहिए। यह बाधा गणितीय रूप से निम्नानुसार लिखी जा सकती है -
$$ \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j} \ _: = \: 1 \: for \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $
अब ऊर्जा को कम करने के लिए, उपरोक्त बाधा के आधार पर, इसमें एक शब्द अनुपात होगा -
$$ \ displaystyle \ sum \ limit_ {j = 1} ^ n \ left (\ start {array} {c} 1 \: - \: \ displaystyle \ sum \ limit_ {x = 1} ^ n M_ {x, j) } \ अंत {सरणी} \ right) ^ 2 $$
लागत समारोह गणना
मान लीजिए कि एक चौकोर मैट्रिक्सn × n) द्वारा चिह्नित C के लिए TSP की लागत मैट्रिक्स को दर्शाता है n शहर जहां n > 0। लागत फ़ंक्शन की गणना करते समय कुछ पैरामीटर निम्नलिखित हैं -
Cx, y - लागत मैट्रिक्स का तत्व शहर से यात्रा की लागत को दर्शाता है x सेवा y।
ए और बी के तत्वों की निकटता निम्नलिखित संबंध द्वारा दिखाई जा सकती है -
$ $ M_ {x, i} \: = \: 1 \: \: और \: \: M_ {y, i \ pm 1} \: = \: 1 $ $
जैसा कि हम जानते हैं, मैट्रिक्स में प्रत्येक नोड का आउटपुट मान 0 या 1 हो सकता है, इसलिए शहरों ए के प्रत्येक जोड़े के लिए, बी हम निम्नलिखित फ़ंक्शन को ऊर्जा फ़ंक्शन में जोड़ सकते हैं -
$$ \ displaystyle \ sum \ limit_ {i = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \ _: + \ _: M_ {y, i-1}) $$
उपरोक्त लागत फ़ंक्शन और बाधा मूल्य के आधार पर, अंतिम ऊर्जा फ़ंक्शन E इस प्रकार दिया जा सकता है -
$ $ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limit_ {i = 1} ^ n \ displaystyle \ sum \ limit_ {x} \ displaystyle \ sum \ limit_ {y neq x} C_ {एक्स, वाई} M_ {x, मैं} (M_ {y, i + 1} \: + \: M_ {y i-1}) \: + $$
$$ \: \ start {bmatrix} \ Gamma_ {1} \ displaystyle \ sum \ limit_ {x} \ left (\ start {array} {c} 1 \ _: - \: \ displaystyle \ sum \ limit_ i_ M_) {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limit_ {i} \ बाएँ (\ शुरू {सरणी} {c} 1 \ _: \ _ : \ displaystyle \ sum \ limit_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$
यहाँ, γ1 तथा γ2 दो वजन वाले स्थिरांक हैं।