इंडक्टर्स में सर्किट कनेक्शन
एक इंडक्टर जब एक सर्किट में जुड़ा होता है, तो वह कनेक्शन श्रृंखला या समानांतर हो सकता है। आइए अब जानते हैं कि कुल धारा, वोल्टेज और प्रतिरोध मानों का क्या होगा यदि वे श्रृंखला में जुड़े हुए हैं, जब समानांतर में जुड़े हुए हैं।
श्रृंखला में संकेतक
आइए देखें कि क्या होता है, जब कुछ प्रेरक श्रृंखला में जुड़े होते हैं। आइए विभिन्न मानों के साथ तीन प्रतिरोधों पर विचार करें, जैसा कि नीचे दिए गए आंकड़े में दिखाया गया है।
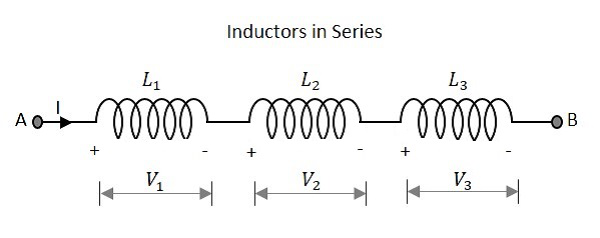
अधिष्ठापन
एक सर्किट श्रृंखला श्रोताओं वाले कुल अधिष्ठापन व्यक्ति के योग के योग के बराबर है। ऊपर दिए गए नेटवर्क का कुल अधिष्ठापन मूल्य है
$$ L_ {टी} \: \: = \: \: L_ {1} \: \: + \: \: L_ {2} \: \: + \: \: L_ {3} $$
जहाँ L 1 1 सेंट रेसिस्टर का इंडक्शन है, L 2 2 एन डी रेसिस्टर का इंडक्शन है और एल 3 उपरोक्त नेटवर्क में 3 आरडी रेसिस्टर का इंडक्शन है ।
वोल्टेज
सीरीज़ इंडक्टर्स नेटवर्क में दिखाई देने वाली कुल वोल्टेज प्रत्येक इंडिविजुअल इंडक्शन पर वोल्टेज ड्रॉप्स के अतिरिक्त होती है।
कुल वोल्टेज जो सर्किट में दिखाई देता है
$$ वी \: \: = \: \: V_ {1} \: \: + \: \: V_ {2} \: \: + \: \: V_ {3} $$
जहाँ V 1 , 1 सेंट प्रारंभ करनेवाला के पार वोल्टेज ड्रॉप है , V 2 , 2 nd प्रारंभ करनेवाला के पार वोल्टेज ड्रॉप है और V 3 उपरोक्त नेटवर्क में 3 rd प्रारंभ करनेवाला के पार वोल्टेज ड्रॉप है।
वर्तमान
वर्तमान की कुल राशि जो श्रृंखला में जुड़े प्रेरकों के एक सेट से बहती है, पूरे नेटवर्क में सभी बिंदुओं पर समान है।
नेटवर्क के माध्यम से वर्तमान
$$ मैं \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
जहाँ मैं 1 को 1 सेंट प्रारंभ करनेवाला के माध्यम से चालू करता हूँ, I 2 को 2 nd प्रारंभ करनेवाला के माध्यम से वर्तमान है और I 3 उपरोक्त नेटवर्क में 3 rd प्रारंभ करनेवाला के माध्यम से वर्तमान है ।
समानांतर में संकेतक
आइए देखें कि क्या होता है, जब कुछ प्रतिरोध समानांतर में जुड़े होते हैं। आइए विभिन्न मानों के साथ तीन प्रतिरोधों पर विचार करें, जैसा कि नीचे दिए गए आंकड़े में दिखाया गया है।

अधिष्ठापन
समानांतर प्रतिरोधों वाले सर्किट के कुल अधिष्ठापन की गणना श्रृंखला प्रारंभ करनेवाला नेटवर्क विधि से अलग तरीके से की जाती है। यहां, व्यक्तिगत प्रेरणों के पारस्परिक (1 / आर) मूल्य को कुल प्रेरण मूल्य प्राप्त करने के लिए बीजीय राशि के व्युत्क्रम के साथ जोड़ा जाता है।
नेटवर्क का कुल इंडक्शन वैल्यू है
$$ \ frac {1} {{L_ टी}} \: \: = \: \: \ frac {1} {L_ {1}} \: \: + \: \: \ frac {1} {{L_ 2}} \: \: + \: \: \ frac {1} {L_ {3}} $$
जहाँ L 1 , 1 सेंट प्रारंभ करनेवाला का अधिष्ठापन है , L 2 2 nd प्रारंभ करनेवाला का प्रेरण है और L 3 उपरोक्त नेटवर्क में 3 rd प्रारंभ करनेवाला का अधिष्ठापन है ।
समानांतर प्रेरण की गणना के लिए हमारे पास जो विधि है, हम दो-प्रारंभ करनेवाला समानांतर नेटवर्क के लिए एक सरल समीकरण प्राप्त कर सकते हैं। यह है
$ $ L_ {T} \: \: = \: \: \ frac {L_ {1} \ _: \: \ टाइम्स \: \: L_ {2}} {L_ {1} \: \: + \: \ _ : L_ {2}} $ $
वोल्टेज
कुल वोल्टेज जो एक समानांतर प्रेरक नेटवर्क में दिखाई देता है, वही वोल्टेज प्रत्येक व्यक्तिगत अधिष्ठापन पर गिरता है।
वह वोल्टेज जो पूरे सर्किट में दिखाई देता है
$$ वी \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
जहाँ V 1 , 1 सेंट प्रारंभ करनेवाला के पार वोल्टेज ड्रॉप है , V 2 , 2 nd प्रारंभ करनेवाला के पार वोल्टेज ड्रॉप है और V 3 उपरोक्त नेटवर्क में 3 rd प्रारंभ करनेवाला के पार वोल्टेज ड्रॉप है। इसलिए वोल्टेज एक समानांतर प्रारंभ करनेवाला नेटवर्क के सभी बिंदुओं पर समान है।
वर्तमान
एक समानांतर प्रेरक नेटवर्क में प्रवेश करने वाली वर्तमान की कुल राशि सभी समानांतर शाखाओं में बहने वाली सभी व्यक्तिगत धाराओं का योग है। प्रत्येक शाखा का अधिष्ठापन मूल्य उस धारा के मूल्य को निर्धारित करता है जो इसके माध्यम से बहती है।
नेटवर्क के माध्यम से कुल करंट है
$$ मैं \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
जहाँ मैं 1 को 1 सेंट प्रारंभ करनेवाला के माध्यम से चालू करता हूँ, I 2 को 2 nd प्रारंभ करनेवाला के माध्यम से वर्तमान है और I 3 उपरोक्त नेटवर्क में 3 rd प्रारंभ करनेवाला के माध्यम से वर्तमान है ।
इसलिए अलग-अलग शाखाओं में अलग-अलग धाराओं का योग एक समानांतर नेटवर्क में कुल वर्तमान प्राप्त करता है।
आगमनात्मक प्रतिक्रिया
इंडक्टिव रिऐक्टेंस एक प्रारंभकर्ता द्वारा प्रत्यावर्ती धारा प्रवाह या बस एसी करंट द्वारा प्रस्तुत विपक्ष है। एक प्रारंभ करनेवाला के पास वर्तमान के प्रवाह में परिवर्तन का विरोध करने की संपत्ति होती है और इसलिए यह कुछ विरोध को दर्शाता है जिसे इसे समाप्त किया जा सकता हैreactance, क्योंकि इनपुट वर्तमान की आवृत्ति को इसके प्रतिरोध के साथ भी माना जाना चाहिए।
संकेत - XL
इकाइयाँ - Ohms
प्रतीक - Ω
विशुद्ध रूप से आगमनात्मक सर्किट में, करंट IL lagsलागू वोल्टेज 90 ° से। आगमनात्मक प्रतिक्रिया की गणना किसके द्वारा की जाती है,
$ $ X_ {L} \: \: = \: \: 2 \ pi fL $ $
जहाँ f सिग्नल की फ्रीक्वेंसी है। इसलिए आगमनात्मक प्रतिक्रिया आवृत्ति और अधिष्ठापन का एक कार्य है।