मूल इलेक्ट्रॉनिक्स - अनिच्छा
वर्तमान प्रवाह के परिवर्तन से प्रेरित वोल्टेज प्राप्त करने के लिए एक प्रारंभ करनेवाला की संपत्ति को इंडक्शन के रूप में परिभाषित किया गया है। Inductance वोल्टेज के अनुपात में करंट के परिवर्तन की दर है।
वर्तमान के परिवर्तन की दर चुंबकीय क्षेत्र में परिवर्तन का उत्पादन करती है, जो वोल्टेज स्रोत के विपरीत ईएमएफ को प्रेरित करती है। EMF के प्रेरण की इस संपत्ति को कहा जाता हैInductance।
अधिष्ठापन का सूत्र है
$$ उपपादन \: \: = \: \: \ frac {volatge} {दर \: के \: परिवर्तन \: के \: वर्तमान} $$
Units −
Inductance की इकाई है Henry। इसके द्वारा इंगित किया जाता हैL।
प्रेरक अधिकतर mH (मिली हेनरी) और μH (माइक्रो हेनरी) में उपलब्ध हैं।
कहा जाता है कि एक कुंडल का एक अधिष्ठापन होता है one Henry जब की ई.एम.एफ. one volt कुंडली में स्व-प्रेरित होता है, जहां की दर से प्रवाहित धारा में परिवर्तन होता है one ampere per second।
आत्म प्रेरण
यदि एक कुंडली मानी जाती है जिसमें कुछ करंट प्रवाहित होता है, तो इसमें कुछ चुंबकीय क्षेत्र है, जो वर्तमान प्रवाह के लंबवत है। जब यह धारा बदलती रहती है, तो चुंबकीय क्षेत्र भी बदल जाता है और यह परिवर्तनशील चुंबकीय क्षेत्र, स्रोत वोल्टेज के विपरीत, EMF को प्रेरित करता है। उत्पादित ईएमएफ का यह विरोध हैself-induced voltage और इस विधि को कहा जाता है self-inductance।
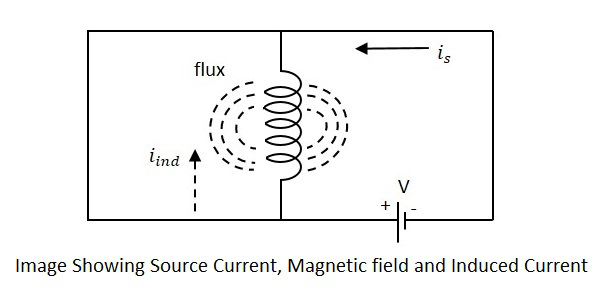
द करेंट is जबकि वर्तमान में आंकड़ा संकेत मिलता है iindप्रेरित धारा को इंगित करता है। प्रवाह कुंडल के चारों ओर बनाए गए चुंबकीय प्रवाह का प्रतिनिधित्व करता है। वोल्टेज के आवेदन के साथ, वर्तमानisप्रवाह और प्रवाह निर्मित होता है। जब करंट लगाis बदलता रहता है, प्रवाह अलग-अलग उत्पादन करता है iind।
कुंडल भर में यह प्रेरित EMF वर्तमान में परिवर्तन की दर के लिए आनुपातिक है। वर्तमान में परिवर्तन की दर जितनी अधिक होगी ईएमएफ प्रेरित मूल्य उतना अधिक होगा।
हम उपरोक्त समीकरण को इस प्रकार लिख सकते हैं
$$ ई \: \: \ अल्फा \: \: \ frac {डि} {} डीटी $$
$$ ई \: \: = \: \ एल \: \: \ frac {डि} {} डीटी $$
कहाँ पे,
E ईएमएफ का उत्पादन किया जाता है
dI/dt वर्तमान के परिवर्तन की दर को इंगित करता है
L इंडक्शन के सह-कुशल को इंगित करता है।
सेल्फ-इंडिविजेंस या सेल्फ-इंप्रूवमेंट को-एफिशिएंसी कहा जा सकता है
$$ एल \: \: = \: \: \ frac {ई} {\ frac {डि} {डीटी}} $$
वास्तविक समीकरण के रूप में लिखा गया है
$$ ई \: \: = \: \: - एल \: \: \ frac {डि} {} डीटी $$
उपरोक्त समीकरण में माइनस यह दर्शाता है कि the EMF is induced in opposite direction to the voltage source लेन्ज के नियम के अनुसार।
आपसी अधिष्ठापन
जैसा कि वर्तमान ले जाने वाला कॉइल अपने चारों ओर कुछ चुंबकीय क्षेत्र का उत्पादन करता है, अगर इस कॉइल के पास एक और कॉइल लाया जाता है, जैसे कि यह प्राथमिक के चुंबकीय प्रवाह क्षेत्र में है, तो अलग-अलग चुंबकीय प्रवाह दूसरे कॉइल में एक ईएमएफ को प्रेरित करता है। यदि इस पहले कुंडल को कहा जाता हैPrimary coilदूसरे को एक कहा जा सकता है Secondary coil।
जब प्राथमिक कुंडल के अलग-अलग चुंबकीय क्षेत्र के कारण माध्यमिक कुंडल में ईएमएफ को प्रेरित किया जाता है, तो ऐसी घटना को कहा जाता है Mutual Inductance।
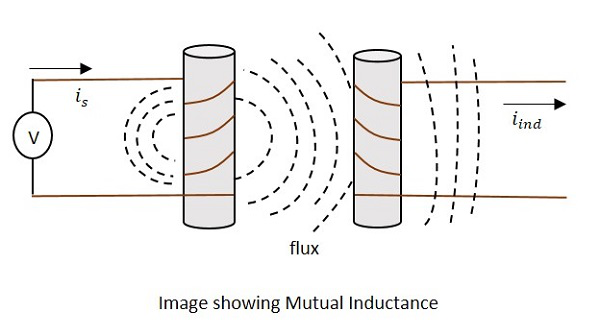
द करेंट is जबकि वर्तमान में आंकड़ा संकेत मिलता है iindप्रेरित धारा को इंगित करता है। प्रवाह कुंडल के चारों ओर बनाए गए चुंबकीय प्रवाह का प्रतिनिधित्व करता है। यह द्वितीयक कॉइल तक भी फैलता है।
वोल्टेज के आवेदन के साथ, वर्तमान isप्रवाह और प्रवाह निर्मित होता है। जब करंट लगाis बदलता रहता है, प्रवाह अलग-अलग उत्पादन करता है iind माध्यमिक कुंडली में, म्युचुअल इंडक्शन प्रॉपर्टी के कारण।
बदलाव इस तरह हुआ।
$$ V_ {पी} \: \: I_ {पी} \ rightArrow \: \: बी \: \: \ rightArrow \: \: V_ {s} \: \: I_ {s} $$
कहाँ पे,
Vp ip क्रमशः वोल्टेज और प्राथमिक कॉइल में वोल्टेज को इंगित करें
B चुंबकीय प्रवाह को इंगित करता है
Vs is क्रमशः वोल्टेज और वर्तमान को द्वितीयक कॉइल में इंगित करें
आपसी अधिष्ठापन M दो सर्किट प्राथमिक की धारा में बदलाव से प्रेरित माध्यमिक में वोल्टेज की मात्रा का वर्णन करते हैं।
$$ V (द्वितीयक) \: \: = \: \: - एम \ फ्राक {\ डेल्टा I} {\ Delta t}
जहां $ \ frac {\ Delta I} {\ Delta t} $ समय के साथ वर्तमान के परिवर्तन की दर और Mम्यूचुअल इंडक्शन का सह-कुशल है। माइनस साइन स्रोत के विपरीत वर्तमान की दिशा को इंगित करता है।
Units −
म्यूचुअल इंडक्शन की इकाइयाँ है
$$ वाल्ट \: \: = \: \: M \ frac {amps} {सेक} $$
(उपरोक्त समीकरण से)
$$ एम \: \: = \: \: \ frac {वाल्ट \:। सेकंड} {} amp $$
$$ = \: \: हेनरी (एच) $$
प्राथमिक और माध्यमिक कॉइल के घुमावों की संख्या के आधार पर, चुंबकीय प्रवाह लिंकेज और प्रेरित ईएमएफ की मात्रा भिन्न होती है। प्राथमिक में घुमावों की संख्या N1 द्वारा और द्वितीयक N2 द्वारा निरूपित की जाती है। युग्मन का सह-कुशल वह शब्द है जो दो कुंडलियों के पारस्परिक अधिष्ठापन को निर्दिष्ट करता है।
अनिद्रा को प्रभावित करने वाले कारक
कुछ कारक हैं जो एक प्रारंभ करनेवाला के प्रदर्शन को प्रभावित करते हैं। प्रमुख नीचे चर्चा कर रहे हैं।
कुंडल की लंबाई
प्रारंभ करनेवाला कॉइल की लंबाई कॉइल की प्रेरण के विपरीत आनुपातिक है। यदि कुंडली की लंबाई अधिक है, तो उस प्रारंभकर्ता द्वारा दिए गए अधिष्ठापन कम हो जाता है और इसके विपरीत।
कॉइल के अनुभागीय क्षेत्र को पार करें
कॉइल का क्रॉस सेक्शनल एरिया सीधे कॉइल के इंडक्शन के समानुपाती होता है। कॉइल का क्षेत्रफल जितना अधिक होगा, इंडक्शन भी उतना ही अधिक होगा।
घुमावों की संख्या
घुमावों की संख्या के साथ, कुंडल सीधे प्रेरण को प्रभावित करता है। कुंडली में घुमावों की संख्या के लिए अधिष्ठापन का मूल्य वर्ग हो जाता है। इसलिए, घुमावों की संख्या जितनी अधिक होगी, इसका वर्ग कुंडल के अधिष्ठापन का मूल्य होगा।
कोर की पारगम्यता
permeability (μ)प्रारंभ करनेवाला की मुख्य सामग्री इंगित करती है कि कोर अपने भीतर एक चुंबकीय क्षेत्र के गठन के लिए समर्थन प्रदान करता है। higher कोर सामग्री की पारगम्यता, higher इंडक्शन होगा।
युग्मन का गुणांक
यह दो कॉइल के पारस्परिक अधिष्ठापन की गणना के लिए जाना जाने वाला एक महत्वपूर्ण कारक है। आइए हम क्रमशः एन 1 और एन 2 के दो पास के कोयल्स पर विचार करें।
पहले कुंडल मैं के माध्यम से वर्तमान 1 कुछ प्रवाह Ψ पैदा करता है 1 । वेबर-टर्न द्वारा चुंबकीय प्रवाह लिंकेज की मात्रा को समझा जाता है।
दूसरे का तार करने के लिए चुंबकीय प्रवाह लिंकेज की राशि दो, मैं की इकाई चालू की वजह से 1 हो
$$ \ frac {N_ {2} \ varphi_ {1}} {I_ {1}} $$
इसे म्यूचुअल इंडक्शन के सह-कुशल के रूप में समझा जा सकता है, जिसका अर्थ है
$$ एम \: \: = \: \: \ frac {N_ {2} \ varphi_ {1}} {I_ {1}} $$
इसलिए दो कॉइल या सर्किट के बीच म्यूचुअल इंडक्शन के सह-कुशल को दूसरे कॉइल में करंट के 1 ए के कारण एक कॉइल में वेबर-टर्न के रूप में समझा जाता है।
यदि पहले कॉइल का स्व-अधिष्ठापन एल 1 है , तो
$$ L_ {1} I_ {1} \: \: = \: \: {N_ {1} \ varphi_ {1}} \: \: => \: \: \ frac {L_ {1}} {N_ {1}} \: \: \ frac {\ varphi_ {1}} {I_ {1}} $$
$$ एम \: \: = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} $$
इसी तरह, दूसरे कॉइल में करंट आई 2 के कारण आपसी इंडक्शन का गुणांक है
$$ एम \: \: = \: \: \ frac {N_ {1} \ varphi_ {2}} {I_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \ : 1 $$
यदि दूसरे कुंडल का स्व-अधिष्ठापन एल 2 है
$$ L_ {2} I_ {2} \: \: = \: \: N_ {2} \ varphi_ {2} $$
$$ \ frac {L_ {2}} {N_ {2}} \: \: = \: \: \ frac {\ varphi_ {2}} {I_ {2}} $$
इसलिए,
$$ एम \: \: = \: \: \ frac {N_ {1} L_ {2}} {N_ {2}} \: \ dotsm \: \ dotsm \: \ dotsm \: \ dotsm \: \: 2 $$
1 और 2 को गुणा करते हुए, हम प्राप्त करते हैं
$$ एम \: \: \ बार \: \: एम = \: \: \ frac {N_ {2} L_ {1}} {N_ {1}} \: \: \ बार \: \: \ frac { N_ {1} L_ {2}} {N_ {2}} $$
$$ एम ^ {2} \: \: = \: \: L_ {1} L_ {2} \: \: => \: \: M \: \: = \: \: \ sqrt {{1 L_ } L_ {2}} $$
उपरोक्त समीकरण तब सही होता है जब प्राथमिक कॉइल के पूरे बदलते प्रवाह को माध्यमिक कॉइल के साथ जोड़ा जाता है, जो एक आदर्श मामला है। लेकिन व्यवहार में, यह मामला नहीं है। इसलिए, हम इस प्रकार लिख सकते हैं
$$ एम \: \: \ neq \: \: \ sqrt {L_ {1} L_ {2}} $$
$ $ और \ frac {M} {\ sqrt {L_ {1} L_ {2}}}: \: \: = \: \: K \: \ \: \ neq \: \: 1 $ $
जहाँ K को युग्मन के गुणांक के रूप में जाना जाता है।
Coefficient of coupling K पारस्परिक प्रेरण के वास्तविक गुणांक के अनुपात के रूप में परिभाषित किया जा सकता है आदर्श (अधिकतम) गुणांक के आपसी समन्वय।
यदि k का मान एकता के निकट है, तो कॉइल्स को कसकर युग्मित कहा जाता है और यदि k = 0 का मान है, तो कॉइल्स को शिथिल रूप से युग्मित कहा जाता है।
इंडक्टर्स के अनुप्रयोग
Inductors के कई अनुप्रयोग हैं, जैसे -
उच्च आवृत्ति वाले घटकों को समझने और शोर संकेतों को दबाने के लिए फिल्टर सर्किट में इंडक्टर्स का उपयोग किया जाता है
अवांछित एचएफ संकेतों से सर्किट को अलग करना।
एक सर्किट बनाने और स्पाइक्स से सर्किट को अलग करने के लिए बिजली के सर्किट में इंडक्टर्स का उपयोग किया जाता है।
प्रेरकों का उपयोग मोटरों में भी किया जाता है।