प्रतिरोधों में सर्किट कनेक्शन
एक सर्किट में कनेक्ट होने पर एक रिसिस्टर, वह कनेक्शन या तो श्रृंखला या समानांतर हो सकता है। आइए अब जानते हैं कि कुल धारा, वोल्टेज और प्रतिरोध मानों का क्या होगा यदि वे श्रृंखला में जुड़े हुए हैं, जब समानांतर में जुड़े हुए हैं।
श्रृंखला में प्रतिरोधक
आइए देखें कि क्या होता है, जब कुछ प्रतिरोधक श्रृंखला में जुड़े होते हैं। आइए विभिन्न मानों के साथ तीन प्रतिरोधों पर विचार करें, जैसा कि नीचे दिए गए आंकड़े में दिखाया गया है।
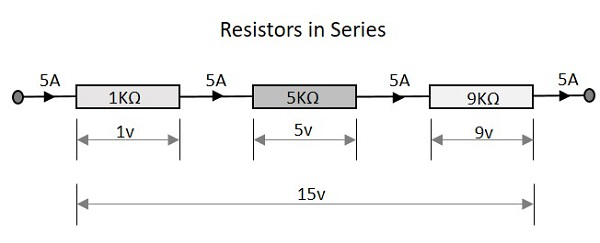
प्रतिरोध
श्रृंखला प्रतिरोधों वाले सर्किट का कुल प्रतिरोध व्यक्तिगत प्रतिरोधों के योग के बराबर होता है। इसका मतलब है कि, उपरोक्त आंकड़े में क्रमशः 1K 5, 5K 9 और 9KΩ मूल्यों वाले तीन प्रतिरोधक हैं।
रोकनेवाला नेटवर्क का कुल प्रतिरोध मान है -
$$ आर \: \: = \: \: R_ {1} \: + \: R_ {2} \: + \: R_ {3} $$
जिसका अर्थ है 1 + 5 + 9 = 15KΩ कुल प्रतिरोध है।
जहाँ R 1 , 1 सेंट प्रतिरोधक का प्रतिरोध है, वहीं R 2 2 nd प्रतिरोधक का प्रतिरोध है और R 3 उपरोक्त प्रतिरोधक नेटवर्क में 3 rd प्रतिरोधक का प्रतिरोध है।
वोल्टेज
सीरीज़ रेसिस्टर्स नेटवर्क में दिखाई देने वाली कुल वोल्टेज, प्रत्येक अलग-अलग रेसिस्टेंस पर वोल्टेज ड्रॉप्स का जोड़ होती है। उपरोक्त आकृति में हमारे पास तीन अलग-अलग प्रतिरोधक हैं जिनके प्रत्येक चरण में वोल्टेज ड्रॉप के तीन अलग-अलग मूल्य हैं।
कुल वोल्टेज जो सर्किट में दिखाई देता है -
$$ वी \: \: = \: \: V_ {1} \: + \: V_ {2} \: + \: V_ {3} $$
जिसका अर्थ है 1v + 5v + 9v = 15v कुल वोल्टेज है।
जहां वी 1 1 सेंट रोकनेवाला का वोल्टेज ड्रॉप है, वहीं वी 2 2 एनडी रेसिस्टर का वोल्टेज ड्रॉप है और वी 3 उपरोक्त अवरोधक नेटवर्क में 3 आरडी रोकनेवाला का वोल्टेज ड्रॉप है ।
वर्तमान
वर्तमान की कुल राशि जो श्रृंखला में जुड़े प्रतिरोधों के एक सेट से बहती है, पूरे अवरोधक नेटवर्क पर सभी बिंदुओं पर समान है। इसलिए इनपुट पर या किसी प्रतिरोध के बीच या आउटपुट पर भी मापा जाने पर करंट समान 5A है।
नेटवर्क के माध्यम से वर्तमान -
$$ मैं \: \: = \: \: I_ {1} \: = \: I_ {2} \: = \: I_ {3} $$
जिसका मतलब है कि सभी बिंदुओं पर करंट 5A है।
जहाँ मैं 1 1 सेंट रेसिस्टर के माध्यम से करंट है, वहीं I 2 , 2 एन डी रेसिस्टर के माध्यम से करंट है और I 3 , उपरोक्त रेसिस्टर नेटवर्क में 3 rd रेसिस्टर के माध्यम से करंट है ।
समानांतर में प्रतिरोध
आइए देखें कि क्या होता है, जब कुछ प्रतिरोध समानांतर में जुड़े होते हैं। आइए विभिन्न मानों के साथ तीन प्रतिरोधों पर विचार करें, जैसा कि नीचे दिए गए आंकड़े में दिखाया गया है।
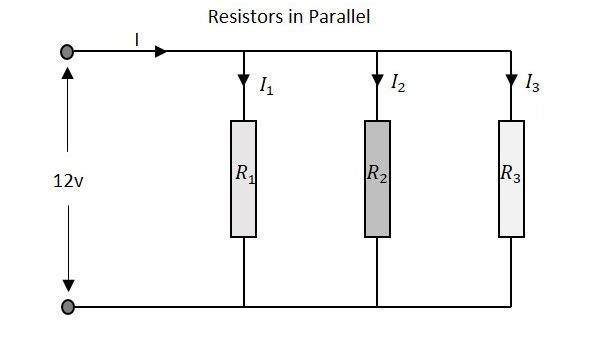
प्रतिरोध
समानांतर प्रतिरोधों वाले सर्किट के कुल प्रतिरोध की गणना श्रृंखला रोकनेवाला नेटवर्क विधि से अलग तरीके से की जाती है। यहां, कुल प्रतिरोध मूल्य प्राप्त करने के लिए बीजीय योग के व्युत्क्रम के साथ व्यक्तिगत प्रतिरोधों के पारस्परिक (1 / आर) मूल्य को जोड़ा जाता है।
रोकनेवाला नेटवर्क का कुल प्रतिरोध मान है -
$$ \ frac {1} {R} \: \: = \: \: \ frac {1} {R_ {1}} \: \: + \: \: \ frac {1} {R_ {2}} \: \: + \ frac {1} {R_ {3}} $$
जहाँ R 1 , 1 सेंट प्रतिरोधक का प्रतिरोध है, वहीं R 2 2 nd प्रतिरोधक का प्रतिरोध है और R 3 उपरोक्त प्रतिरोधक नेटवर्क में 3 rd प्रतिरोधक का प्रतिरोध है।
उदाहरण के लिए, यदि पिछले उदाहरण के प्रतिरोध मानों को माना जाता है, जिसका अर्थ है R 1 = 1K R, R 2 = 5K = और R 3 = 9K 3 । समानांतर प्रतिरोधक नेटवर्क का कुल प्रतिरोध होगा -
$$ \ frac {1} {R} \: \: = \: \: \ frac {1} {1} \: \: + \: \: \ frac {1} {5} \: \: + \ frac {1} {9} $$
$$ = \: \: \ frac {45 \: \: + \: \: 9 \: \: + \: \: 5} {45} \: \: = \: \: \ frac {59} { 45} $$
$$ आर \: \: = \: \: \ frac {45} {59} \: \: = \: \: 0.762K \ ओमेगा \: \: = \: \: 76.2 \ ओमेगा $$
समानांतर प्रतिरोध की गणना करने के लिए हमारे पास मौजूद विधि से, हम दो-प्रतिरोधक समानांतर नेटवर्क के लिए एक सरल समीकरण प्राप्त कर सकते हैं। यह है -
$$ आर \: \: = \: \: \ frac {R_ {1} \: \: \ बार \: \: R_ {2}} {R_ {1} \: \: + \: \: r_ { 2}} \: $$
वोल्टेज
एक समानांतर रेसिस्टर्स नेटवर्क में दिखाई देने वाली कुल वोल्टेज वैसी ही होती है जैसे वोल्टेज प्रत्येक व्यक्तिगत प्रतिरोध पर गिरती है।
वह वोल्टेज जो पूरे सर्किट में दिखाई देता है -
$$ वी \: \: = \: \: V_ {1} \: = \: V_ {2} \: = \: V_ {3} $$
जहां वी 1 1 सेंट रोकनेवाला का वोल्टेज ड्रॉप है, वहीं वी 2 2 एनडी रेसिस्टर का वोल्टेज ड्रॉप है और वी 3 उपरोक्त अवरोधक नेटवर्क में 3 आरडी रोकनेवाला का वोल्टेज ड्रॉप है । इसलिए वोल्टेज एक समानांतर रोकनेवाला नेटवर्क के सभी बिंदुओं पर समान है।
वर्तमान
एक समानांतर प्रतिरोधक नेटवर्क में प्रवेश करने वाली वर्तमान की कुल राशि सभी समानांतर शाखाओं में बहने वाली सभी व्यक्तिगत धाराओं का योग है। प्रत्येक शाखा का प्रतिरोध मूल्य वर्तमान के मूल्य को निर्धारित करता है जो इसके माध्यम से बहता है। नेटवर्क के माध्यम से कुल करंट है
$$ मैं \: \: = \: \: I_ {1} \: + \: I_ {2} \: + \: I_ {3} $$
जहाँ मैं 1 1 सेंट रेसिस्टर के माध्यम से करंट है, वहीं I 2 , 2 एन डी रेसिस्टर के माध्यम से करंट है और I 3 , उपरोक्त रेसिस्टर नेटवर्क में 3 rd रेसिस्टर के माध्यम से करंट है । इसलिए विभिन्न शाखाओं में अलग-अलग धाराओं का योग एक समानांतर प्रतिरोधक नेटवर्क में कुल वर्तमान प्राप्त करता है।
एक रेसिस्टर का उपयोग विशेष रूप से कई सर्किटों के आउटपुट में लोड के रूप में किया जाता है। यदि सभी प्रतिरोधक लोड का उपयोग नहीं किया जाता है, तो एक प्रतिरोधक को लोड से पहले रखा जाता है। किसी भी सर्किट में आमतौर पर एक मूल घटक होता है।