उत्तल अनुकूलन - मिनीमा और मैक्सिमा
स्थानीय छोटा या छोटा
$ \ bar {x} \ in \: S $ को किसी फ़ंक्शन का स्थानीय मिनीमा $ फ $ कहा जाता है यदि $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ forall x \ N_ \ varepsilon \ बाएँ (\ bar {x} \ right) $ में जहाँ $ N_ \ varepsilon \ left (\ bar {x} \ right) $ का अर्थ है $ \ bar का पड़ोस {x} $, अर्थात, $ N_ \ varepsilon \ left (\ bar {x} \ right) $ का अर्थ $ \ left \ _ है x- \ bar {x} \ right \ | <\ varepsilon $
स्थानीय मैक्सिमा या मैक्सिमाइज़र
$ \ बार {x} \ in \: S $ को फ़ंक्शन की स्थानीय अधिकतम सीमा $ f $ कहा जाता है यदि $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ forall x \ N_ \ varepsilon \ बाएँ (\ bar {x} \ right) $ में जहाँ $ N_ \ varepsilon \ left (\ bar {x} \ right) $ का अर्थ है $ \ bar का पड़ोस {x} $, अर्थात, $ N_ \ varepsilon \ left (\ bar {x} \ right) $ का अर्थ $ \ left \ _ है x- \ bar {x} \ right \ | <\ varepsilon $
वैश्विक मिनीमा
$ \ bar {x} \ in \: S $ को एक फ़ंक्शन की वैश्विक मिनिमा कहा जाता है $ f $ अगर $ f \ left (\ bar {x} \ right) \ leq f \ left (x \ right), \ S $ में forall x \ _
वैश्विक मैक्सिमा
$ \ bar {x} \ in \: S $ को एक फ़ंक्शन की वैश्विक अधिकतम सीमा कहा जाता है $ f $ अगर $ f \ left (\ bar {x} \ right) \ geq f \ left (x \ right), \ S $ में forall x \ _
उदाहरण
Step 1- स्थानीय मिनीमा और $ f \ बाएँ (\ bar {x} \ right) = का अधिकतम पता लगाएं x ^ 2-4 \ right | $
Solution -

उपरोक्त फ़ंक्शन के ग्राफ से, यह स्पष्ट है कि स्थानीय मिनीमा $ x = \ pm 2 $ और स्थानीय मैक्सिमा $ x = 0 $ पर होता है।
Step 2- वैश्विक मिनिमा एफ को $ f \ left (x \ right) = \ बाईं ओर कार्य करें 4x ^ 3-3x ^ 2 + 7 \ right | $
Solution -
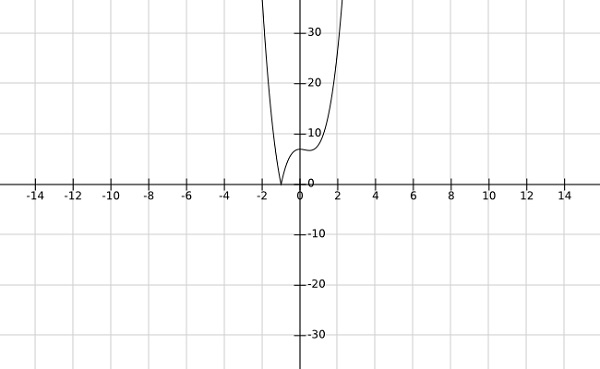
उपरोक्त फ़ंक्शन के ग्राफ से, यह स्पष्ट है कि वैश्विक मिनीमा $ x = -1 $ पर होता है।