डिजिटल संचार - डेल्टा मॉड्यूलेशन
बेहतर नमूने प्राप्त करने के लिए सिग्नल की सैंपलिंग दर Nyquist दर से अधिक होनी चाहिए। अगर अंतर पीसीएम में यह नमूना अंतराल काफी कम हो जाता है, तो नमूना-नमूना आयाम अंतर बहुत छोटा है, जैसा कि कुछ और है1-bit quantization, तो चरण-आकार बहुत छोटा होगा, अर्थात, Δ (डेल्टा)।
डेल्टा मॉड्यूलेशन
मॉडुलन का प्रकार, जहाँ नमूनाकरण दर बहुत अधिक है और जिसमें परिमाणीकरण के बाद के चरण छोटे मूल्य के हैं Δ, इस तरह के एक मॉडुलन के रूप में कहा जाता है delta modulation।
डेल्टा मॉड्यूलेशन की विशेषताएं
डेल्टा मॉड्यूलेशन की कुछ विशेषताएं निम्नलिखित हैं।
सिग्नल सहसंबंध का पूर्ण उपयोग करने के लिए एक अधिक-नमूना इनपुट लिया जाता है।
परिमाणीकरण डिज़ाइन सरल है।
इनपुट अनुक्रम Nyquist दर की तुलना में बहुत अधिक है।
गुणवत्ता मध्यम है।
मॉड्यूलेटर और डेमोडुलेटर का डिज़ाइन सरल है।
आउटपुट तरंग की सीढ़ी-केस सन्निकटन।
चरण-आकार बहुत छोटा है, अर्थात Δ (डेल्टा)।
बिट दर उपयोगकर्ता द्वारा तय किया जा सकता है।
इसमें सरल कार्यान्वयन शामिल है।
डेल्टा मॉड्यूलेशन डीपीसीएम तकनीक का एक सरलीकृत रूप है, जिसे भी देखा जाता है 1-bit DPCM scheme। जैसा कि नमूना अंतराल कम हो जाता है, संकेत सहसंबंध अधिक होगा।
डेल्टा मॉड्यूलेटर
डेल्टा मॉड्यूलेटर में 1-बिट क्वांटाइज़र और दो ग्रीष्मकालीन सर्किट के साथ एक देरी सर्किट शामिल है। निम्नलिखित एक डेल्टा न्यूनाधिक के ब्लॉक आरेख है।
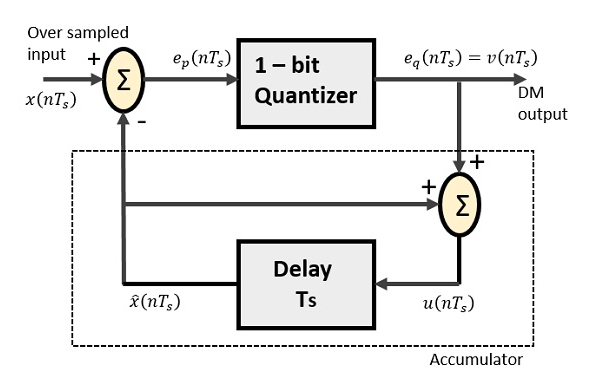
डीपीसीएम में पूर्वसूचक सर्किट को डीएम में सरल विलंब सर्किट से बदल दिया जाता है।
उपरोक्त आरेख से, हमारे पास इस तरह के संकेत हैं -
$ x (nT_ {s}) $ = अधिक नमूना इनपुट
$ e_ {p} (nT_ {s}) $ = समर आउटपुट और क्वांटिज़र इनपुट
$ e_ {q} (nT_ {s}) $ = क्वांटाइज़र आउटपुट = $ v (nT_s) $
$ \ widehat {x} (nT_ {s}) $ = विलंब सर्किट का आउटपुट
$ u (nT_ {s}) $ = विलंब सर्किट का इनपुट
इन सूचनाओं का उपयोग करते हुए, अब हम डेल्टा मॉड्यूलेशन की प्रक्रिया का पता लगाने की कोशिश करेंगे।
$ e_ {p} (nT_ {s}) = x (nT_ {s}) - \ widehat {x} (nT_ {s}) $
--------- समीकरण १
$ = x (nT_ {s}) - u ([n - 1] T_ {s}) $
$ = x (nT_ {s}) - [\ widehat {x} [[n - 1] T_ {s}] + v [[n-1] T_ {s}] $
--------- समीकरण २
आगे की,
$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig। [e_ {p} (nT_ {s})] $
--------- समीकरण ३
$ u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s}) $
कहाँ पे,
$ \ widehat {x} (nT_ {s}) $ = विलंब सर्किट का पिछला मूल्य
$ e_ {q} (nT_ {s}) $ = क्वांटाइज़र आउटपुट = $ v (nT_s) $
अत,
$ u (nT_ {s}) = u ([n-1] T_ {s}) + v (nT_ {s}) $
--------- समीकरण ४
जिसका मतलब है,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
संचय की शून्य स्थिति मानते हुए,
$ u (nT_ {s}) = S \ displaystyle \ sum \ limit_ {j = 1} ^ n sig [e_ {p} (jT_ {s})] $
Accumulated version of DM output = $ \ displaystyle \ sum \ limit_ {j = 1} ^ nv (jT_ {s}) $
--------- समीकरण ५
अब, ध्यान दें
$ \ widehat {x} (nT_ {s}) = u ([n-1] T_ {s}) $
$ = \ displaystyle \ sum \ limit_ {j = 1} ^ {n - 1} v (jT_ {s}) $
--------- समीकरण ६
देरी इकाई उत्पादन एक नमूना द्वारा एक संचायक आउटपुट लैगिंग है।
5 और 6 समीकरणों से, हमें डीमोडुलेटर के लिए एक संभावित संरचना मिलती है।
एक स्टैरे-केस सन्निकट तरंग, डेल्टा मॉड्यूलेटर के आउटपुट के साथ स्टेप-साइज डेल्टा के रूप में होगा (Δ)। तरंग की उत्पादन गुणवत्ता मध्यम है।
डेल्टा डेमोडुलेटर
डेल्टा डेमोडुलेटर में एक कम पास फिल्टर, एक गर्मी और एक देरी सर्किट शामिल हैं। भविष्यवक्ता सर्किट को यहां समाप्त कर दिया गया है और इसलिए डिमॉड्युलेटर को कोई ग्रहणित इनपुट नहीं दिया गया है।
निम्नलिखित डेल्टा डिमोडुलेटर के लिए आरेख है।
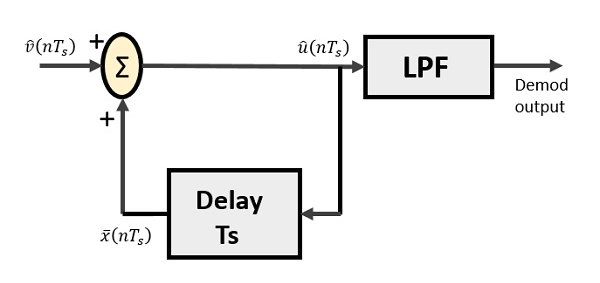
उपरोक्त आरेख से, हमारे पास इस तरह के संकेत हैं -
$ \ widehat {v} (nT_ {s}) $ इनपुट नमूना है
$ \ widehat {u} (nT_ {s}) $ ग्रीष्मकालीन उत्पादन है
$ \ bar {x} (nT_ {s}) $ विलंबित आउटपुट है
एक द्विआधारी अनुक्रम को डीमोडुलेटर के इनपुट के रूप में दिया जाएगा। सीढ़ी-मामला अनुमानित उत्पादन एलपीएफ को दिया जाता है।
कम पास फिल्टर का उपयोग कई कारणों से किया जाता है, लेकिन प्रमुख कारण आउट-ऑफ-बैंड संकेतों के लिए शोर उन्मूलन है। ट्रांसमीटर पर हो सकने वाली चरण-आकार की त्रुटि को कहा जाता हैgranular noise, जो यहां समाप्त हो गया है। यदि कोई शोर मौजूद नहीं है, तो मॉड्यूलेटर आउटपुट डेमोडुलेटर इनपुट के बराबर है।
डीएम ओवर डीपीसीएम के लाभ
1-बिट क्वांटाइज़र
न्यूनाधिक और डिमोडुलेटर का बहुत आसान डिज़ाइन
हालांकि, डीएम में कुछ शोर मौजूद है।
ढलान ओवर लोड विरूपण (जब Δ छोटा है)
दानेदार शोर (जब Δ बड़ा है)
अनुकूली डेल्टा मॉड्यूलेशन (ADM)
डिजिटल मॉड्यूलेशन में, हम चरण-आकार का निर्धारण करने की कुछ समस्या को लेकर आए हैं, जो आउटपुट तरंग की गुणवत्ता को प्रभावित करता है।
मॉड्यूलेटिंग सिग्नल की खड़ी ढलान में एक बड़े स्टेप-साइज़ की ज़रूरत होती है और एक छोटे स्टेपाइज़ की ज़रूरत होती है जहाँ मैसेज में एक छोटा ढलान हो। मिनट का विवरण प्रक्रिया में छूट जाता है। इसलिए, यह बेहतर होगा कि हम अपनी आवश्यकता के अनुसार चरण-आकार के समायोजन को नियंत्रित कर सकें, ताकि वांछित फैशन में नमूना प्राप्त किया जा सके। की अवधारणा हैAdaptive Delta Modulation।
निम्नलिखित अनुगामी डेल्टा न्यूनाधिक का ब्लॉक आरेख है।
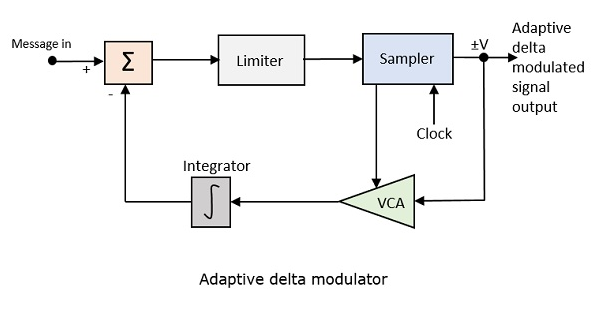
वोल्टेज नियंत्रित एम्पलीफायर का लाभ सैम्पलर से आउटपुट सिग्नल द्वारा समायोजित किया जाता है। एम्पलीफायर लाभ चरण-आकार निर्धारित करता है और दोनों आनुपातिक हैं।
एडीएम वर्तमान नमूने के मूल्य और अगले नमूने के अनुमानित मूल्य के बीच अंतर को निर्धारित करता है। यह तेजी से बदलती मूल्यों के वफादार प्रजनन के लिए, अगले मूल्यों की भविष्यवाणी करने के लिए एक चर चरण ऊंचाई का उपयोग करता है।