डिजिटल संचार - लाइन कोड
ए line codeएक ट्रांसमिशन लाइन पर एक डिजिटल सिग्नल के डेटा ट्रांसमिशन के लिए उपयोग किया जाने वाला कोड है। कोडिंग की इस प्रक्रिया को चुना जाता है ताकि अंतर-प्रतीक हस्तक्षेप जैसे सिग्नल के ओवरलैप और विरूपण से बचने के लिए।
लाइन कोडिंग के गुण
लाइन कोडिंग के गुण निम्नलिखित हैं -
जैसा कि एकल संकेत पर अधिक बिट्स को संचारित करने के लिए कोडिंग की जाती है, उपयोग की जाने वाली बैंडविड्थ बहुत कम हो जाती है।
किसी दिए गए बैंडविड्थ के लिए, शक्ति का कुशलता से उपयोग किया जाता है।
त्रुटि की संभावना बहुत कम हो जाती है।
त्रुटि का पता लगाया जाता है और द्विध्रुवी में भी सुधार की क्षमता होती है।
बिजली घनत्व बहुत अनुकूल है।
समय की सामग्री पर्याप्त है।
के लंबे तार 1s तथा 0s पारदर्शिता बनाए रखने के लिए टाला जाता है।
लाइन कोडिंग के प्रकार
रेखा कोडिंग के 3 प्रकार हैं
- Unipolar
- Polar
- Bi-polar
एकध्रुवीय संकेतन
यूनीपोलर सिग्नलिंग को भी कहा जाता है On-Off Keying या केवल OOK।
नाड़ी की उपस्थिति एक का प्रतिनिधित्व करती है 1 और नाड़ी की अनुपस्थिति एक का प्रतिनिधित्व करती है 0।
यूनिपोलर सिग्नलिंग में दो विविधताएँ हैं -
- नॉन रिटर्न टू जीरो (NRZ)
- ज़ीरो (RZ) पर लौटें
यूनीपोलर नॉन-रिटर्न टू जीरो (NRZ)
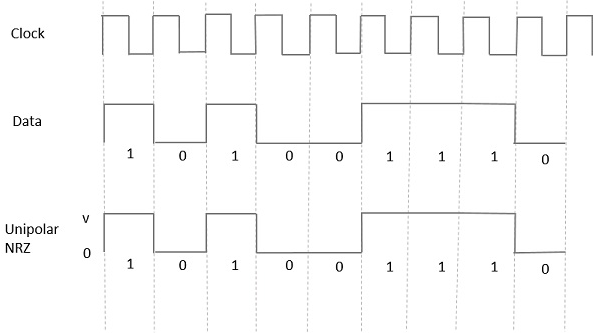
इस प्रकार के एकध्रुवीय संकेतन में, एक उच्च डेटा को एक सकारात्मक पल्स द्वारा दर्शाया जाता है जिसे कहा जाता है Mark, जिसकी एक अवधि है T0प्रतीक बिट अवधि के बराबर। डेटा इनपुट में निम्न में कोई पल्स नहीं है।
निम्न आकृति स्पष्ट रूप से यह दर्शाती है।
Advantages
यूनिपोलर NRZ के फायदे हैं -
- यह आसान है।
- एक कम बैंडविड्थ की आवश्यकता है।
Disadvantages
यूनिपोलर NRZ के नुकसान हैं -
कोई त्रुटि सुधार नहीं हुआ।
कम आवृत्ति घटकों की उपस्थिति संकेत ड्रॉप का कारण हो सकती है।
कोई घड़ी मौजूद नहीं है।
सिंक्रनाइज़ेशन का नुकसान होने की संभावना है (विशेष रूप से लंबे समय के तार के लिए) 1s तथा 0s)।
एकध्रुवीय वापसी शून्य (RZ) के लिए
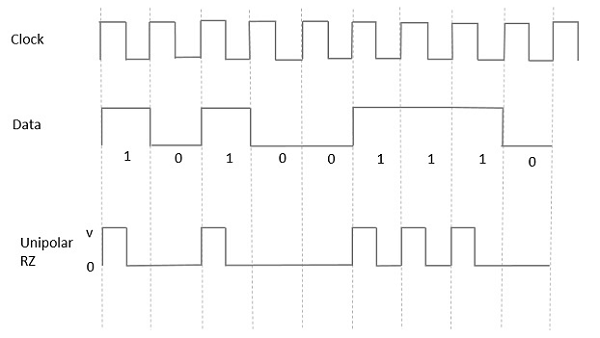
इस प्रकार के एकध्रुवीय संकेतन में, डेटा में एक उच्च, हालांकि एक द्वारा दर्शाया गया है Mark pulse, इसकी अवधि T0प्रतीक की अवधि से कम है। बिट अवधि का आधा हिस्सा उच्च रहता है लेकिन यह तुरंत शून्य पर लौट आता है और शेष अवधि के दौरान पल्स की अनुपस्थिति को दर्शाता है।
यह निम्नलिखित आकृति की मदद से स्पष्ट रूप से समझा जाता है।
Advantages
यूनिपोलर आरजेड के फायदे हैं -
- यह आसान है।
- प्रतीक दर पर मौजूद वर्णक्रमीय रेखा को घड़ी की तरह इस्तेमाल किया जा सकता है।
Disadvantages
यूनिपोलर आरजेड के नुकसान हैं -
- कोई त्रुटि सुधार नहीं।
- दो बार बैंडविड्थ को एकध्रुवीय NRZ के रूप में नियंत्रित करता है।
- सिग्नल ड्रॉप उन स्थानों पर होता है जहां सिग्नल 0 हर्ट्ज पर गैर-शून्य होता है।
ध्रुवीय संकेत
पोलर सिग्नलिंग की दो विधियाँ हैं। वे हैं -
- ध्रुवीय NRZ
- ध्रुवीय RZ
ध्रुवीय NRZ
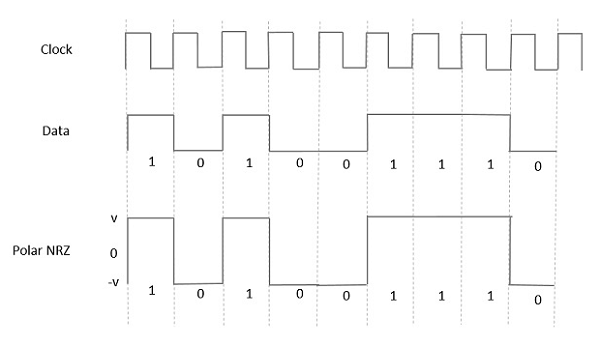
इस प्रकार के पोलर सिगनलिंग में, एक उच्च डेटा को एक सकारात्मक पल्स द्वारा दर्शाया जाता है, जबकि एक डेटा में एक निगेटिव पल्स का प्रतिनिधित्व करता है। निम्न चित्र में यह अच्छी तरह से दर्शाया गया है।
Advantages
पोलर NRZ के फायदे हैं -
- यह आसान है।
- कोई कम-आवृत्ति घटक मौजूद नहीं हैं।
Disadvantages
ध्रुवीय NRZ के नुकसान हैं -
कोई त्रुटि सुधार नहीं।
कोई घड़ी मौजूद नहीं है।
सिग्नल ड्रॉप उन जगहों पर होता है जहां सिग्नल नॉन-जीरो होता है 0 Hz।
ध्रुवीय RZ
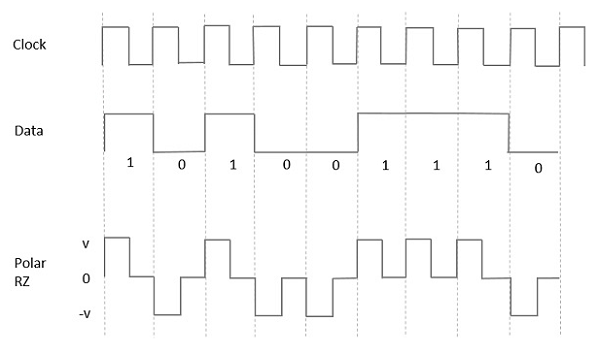
इस प्रकार के ध्रुवीय सिग्नलिंग में, डेटा में एक उच्च, हालांकि एक द्वारा दर्शाया गया है Mark pulse, इसकी अवधि T0प्रतीक की अवधि से कम है। बिट अवधि का आधा हिस्सा उच्च रहता है लेकिन यह तुरंत शून्य पर लौट आता है और शेष अवधि के दौरान पल्स की अनुपस्थिति को दर्शाता है।
हालांकि, कम इनपुट के लिए, एक नकारात्मक पल्स डेटा का प्रतिनिधित्व करता है, और शून्य स्तर बिट अवधि के अन्य आधे हिस्से के लिए समान रहता है। निम्न चित्र में यह स्पष्ट रूप से दर्शाया गया है।
Advantages
पोलर आरजेड के फायदे हैं -
- यह आसान है।
- कोई कम-आवृत्ति घटक मौजूद नहीं हैं।
Disadvantages
ध्रुवीय आरजेड के नुकसान हैं -
कोई त्रुटि सुधार नहीं।
कोई घड़ी मौजूद नहीं है।
ध्रुवीय NRZ के बैंडविड्थ को दोगुना कर देता है।
सिग्नल ड्रॉप उन जगहों पर होता है जहां सिग्नल नॉन-जीरो होता है 0 Hz।
द्विध्रुवी संकेतन
यह एक एन्कोडिंग तकनीक है जिसमें तीन वोल्टेज स्तर होते हैं +, - तथा 0। ऐसे सिग्नल को कहा जाता हैduo-binary signal।
इस प्रकार का एक उदाहरण है Alternate Mark Inversion (AMI)। के लिए1, वोल्टेज स्तर को वैकल्पिक होने से + से - या से - तक एक संक्रमण मिलता है 1sसमान ध्रुवीयता का होना। ए0 शून्य वोल्टेज स्तर होगा।
इस पद्धति में भी, हमारे पास दो प्रकार हैं।
- द्विध्रुवीय NRZ
- द्विध्रुवीय आरजेड
अब तक चर्चा किए गए मॉडलों से, हमने एनआरजेड और आरजेड के बीच अंतर सीखा है। यह यहाँ भी उसी तरह जाता है। निम्न आकृति स्पष्ट रूप से यह दर्शाती है।
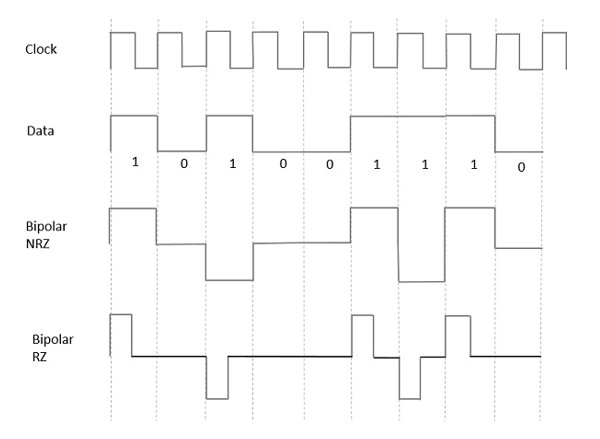
उपरोक्त आंकड़े में द्विध्रुवी NRZ और RZ तरंग दोनों हैं। पल्स अवधि और प्रतीक बिट अवधि NRZ प्रकार में बराबर हैं, जबकि पल्स अवधि RZ प्रकार में प्रतीक बिट अवधि का आधा है।
लाभ
निम्नलिखित फायदे हैं -
यह आसान है।
कोई कम-आवृत्ति घटक मौजूद नहीं हैं।
एकध्रुवीय और ध्रुवीय NRZ योजनाओं की तुलना में कम बैंडविड्थ पर कब्जा करता है।
यह तकनीक एसी युग्मित लाइनों पर संचरण के लिए उपयुक्त है, क्योंकि सिग्नल ड्रोपिंग यहां नहीं होता है।
इसमें एक एकल त्रुटि का पता लगाने की क्षमता मौजूद है।
नुकसान
निम्नलिखित नुकसान हैं -
- कोई घड़ी मौजूद नहीं है।
- डेटा के लंबे तार सिंक्रनाइज़ेशन के नुकसान का कारण बनते हैं।
बिजली की वर्णक्रमीय घनत्व
वह फ़ंक्शन जो वर्णन करता है कि सिग्नल की शक्ति को विभिन्न आवृत्तियों पर कैसे वितरित किया गया, आवृत्ति डोमेन में कहा जाता है Power Spectral Density (PSD)।
PSD ऑटो-सहसंबंध का फूरियर ट्रांसफॉर्म (टिप्पणियों के बीच समानता) है। यह एक आयताकार नाड़ी के रूप में है।
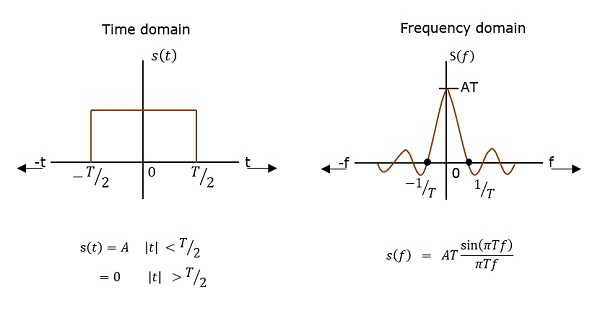
PSD व्युत्पत्ति
आइंस्टीन-वीनर-खिन्टचाइन प्रमेय के अनुसार, यदि एक यादृच्छिक प्रक्रिया के ऑटो सहसंबंध समारोह या पावर वर्णक्रमीय घनत्व ज्ञात है, तो दूसरा बिल्कुल पाया जा सकता है।
इसलिए, पावर वर्णक्रमीय घनत्व को प्राप्त करने के लिए, हम नीचे दिखाए गए अनुसार पावर सिग्नल $ x (t) $ के ऑटो-सहसंबंध $ (R_x (\ tau)) का उपयोग करेंगे।
$_ x (t) x (t + \ tau) dt $
चूंकि $ x (t) $ में आवेग होते हैं, इसलिए $ R_x (\ tau) $ के रूप में लिखा जा सकता है
$ R_x (\ tau) = \ frac {1} {T} \ displaystyle \ sum \ limit_ {n = - \ infty} ^ \ infty R_n \ delta (\ tau - nT) $
जहाँ $ R_n = \ lim_ {N \ rightarrow \ infty} \ frac {1} {N} \ sum_ka_ka_ {k + n} $
वास्तविक संकेतों के लिए $ R_n = R _ {- n} $ का पता होना, हमारे पास है
$ S_x (w) = \ frac {1} {T} (R_0 + 2 \ displaystyle \ sum \ limit_ {n = 1} ^ \ infty R_n \ cos nwT) $
चूंकि पल्स फ़िल्टर में $ (w) \ leftrightarrow f (t) $ का स्पेक्ट्रम है, हमारे पास है
$ s_y (w) = \ mid F (w) \ mid ^ 2S_x (w) $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (\ displaystyle \ sum \ limit_ {n = - \ infty} ^ \ infty R_ne ^ {- jnwT_ {b}}} $
$ = \ frac {\ mid F (w) \ mid ^ 2} {T} (R_0 + 2 \ displaystyle \ sum \ limit_ {n = 1} ^ \ infty R_n \ cos nwT) $
इसलिए, हम पावर स्पेक्ट्रल घनत्व के लिए समीकरण प्राप्त करते हैं। इसका उपयोग करते हुए, हम विभिन्न लाइन कोडों का पीएसडी पा सकते हैं।