स्रोत कोडन प्रमेय
असतत स्मृतिहीन स्रोत द्वारा निर्मित कोड का कुशलता से प्रतिनिधित्व किया जाना चाहिए, जो संचार में एक महत्वपूर्ण समस्या है। ऐसा होने के लिए, कोड शब्द हैं, जो इन स्रोत कोड का प्रतिनिधित्व करते हैं।
उदाहरण के लिए, टेलीग्राफी में, हम मोर्स कोड का उपयोग करते हैं, जिसमें अक्षर द्वारा निरूपित किया जाता है Marks तथा Spaces। यदि पत्रE माना जाता है, जो कि ज्यादातर उपयोग किया जाता है, यह द्वारा निरूपित किया जाता है “.” जबकि पत्र Q जिसका इस्तेमाल शायद ही कभी किया जाता है “--.-”
आइए हम ब्लॉक आरेख पर एक नज़र डालें।
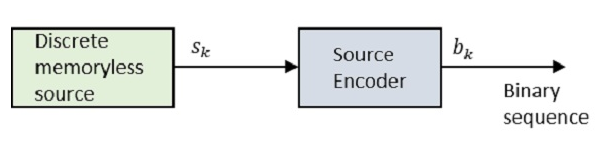
कहाँ पे Sk असतत स्मृतिहीन स्रोत का उत्पादन है और bk स्रोत एनकोडर का आउटपुट होता है जिसे दर्शाया जाता है 0s तथा 1s।
एन्कोडेड अनुक्रम ऐसा है कि यह आसानी से रिसीवर पर डिकोड किया जाता है।
आइए हम मान लें कि स्रोत के पास एक वर्णमाला है k विभिन्न प्रतीकों और है कि kth प्रतीक Sk संभावना के साथ होता है Pk, कहाँ पे k = 0, 1…k-1।
प्रतीक को असाइन किया गया बाइनरी कोड शब्द दें Sk, एनकोडर लंबाई होने से lk, बिट्स में मापा जाता है।
इसलिए, हम स्रोत एनकोडर की औसत कोड शब्द लंबाई L को परिभाषित करते हैं
$$ \ overline {L} = \ displaystyle \ sum \ limit_ {k = 0} ^ {k-1} p_kl_k $$
L प्रति स्रोत प्रतीक बिट्स की औसत संख्या का प्रतिनिधित्व करता है
यदि $ L_ {मिनट} = \: न्यूनतम \: संभव \: मूल्य \: का: \: \ ओवरलाइन {एल} $
फिर coding efficiency के रूप में परिभाषित किया जा सकता है
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
$ \ Overline {L} \ geq L_ {min} $ के साथ हमारे पास $ \ eta \ leq 1 $ होगा
हालांकि, स्रोत एनकोडर को तब कुशल माना जाता है जब $ \ eta = 1 $ हो
इसके लिए $ L_ {min} $ का मूल्य निर्धारित करना होगा।
आइए हम परिभाषा का उल्लेख करते हैं, “एंट्रोपी $ एच (\ डेल्टा) $ के एक असतत स्मृतिहीन स्रोत को देखते हुए, औसत कोड-शब्द की लंबाईL किसी भी स्रोत के लिए एन्कोडिंग को $ \ overline {L} \ geq H (\ delta) $ के रूप में बांधा गया है। "
सरल शब्दों में, कोड शब्द (उदाहरण: QUEUE शब्द के लिए मोर्स कोड है -.- .. .. .. ..-) हमेशा स्रोत कोड (उदाहरण में QUEUE) से अधिक या बराबर होता है। जिसका अर्थ है, कोड शब्द में प्रतीकों स्रोत कोड में वर्णमाला से अधिक या बराबर हैं।
इसलिए $ L_ {min} = H (\ डेल्टा) $ के साथ, Entropy $ H (\ delta) $ के संदर्भ में स्रोत एनकोडर की दक्षता $ के रूप में लिखी जा सकती है
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $ $
इस स्रोत कोडिंग प्रमेय को कहा जाता है noiseless coding theoremके रूप में यह एक त्रुटि मुक्त एन्कोडिंग स्थापित करता है। इसे भी कहा जाता हैShannon’s first theorem।