प्रतिगमन तकनीक
रिग्रेशन एक सांख्यिकीय तकनीक है जो परस्पर आर्थिक चर के बीच संबंधों को योग्य बनाने में मदद करती है। पहले चरण में स्वतंत्र चर के गुणांक का अनुमान लगाना और फिर अनुमानित गुणांक की विश्वसनीयता को मापना शामिल है। इसके लिए एक परिकल्पना तैयार करने की आवश्यकता है, और परिकल्पना के आधार पर, हम एक फ़ंक्शन बना सकते हैं।
यदि कोई प्रबंधक फर्म के विज्ञापन व्यय और उसकी बिक्री राजस्व के बीच संबंध निर्धारित करना चाहता है, तो वह परिकल्पना की परीक्षा से गुजरना होगा। यह मानते हुए कि उच्च विज्ञापन व्यय एक फर्म के लिए उच्च बिक्री का नेतृत्व करते हैं। प्रबंधक एक निश्चित समय में विज्ञापन व्यय और बिक्री राजस्व पर डेटा एकत्र करता है। इस परिकल्पना को गणितीय कार्य में अनुवादित किया जा सकता है, जहां यह होता है -
Y = A + Bx
कहाँ पे Y बिक्री है, x विज्ञापन खर्च है, A तथा B स्थिर हैं।
समारोह में परिकल्पना का अनुवाद करने के बाद, इसके लिए आधार आश्रित और स्वतंत्र चर के बीच संबंध का पता लगाना है। निर्भर चर का मूल्य शोधकर्ताओं के लिए सबसे अधिक महत्वपूर्ण है और अन्य चर के मूल्य पर निर्भर करता है। स्वतंत्र चर का उपयोग आश्रित चर में भिन्नता को समझाने के लिए किया जाता है। इसे दो प्रकारों में वर्गीकृत किया जा सकता है -
Simple regression - एक स्वतंत्र चर
Multiple regression - कई स्वतंत्र चर
सरल प्रतिगमन
प्रतिगमन विश्लेषण का निर्माण करने के लिए निम्नलिखित चरण हैं -
- प्रतिगमन मॉडल निर्दिष्ट करें
- चर पर डेटा प्राप्त करें
- मात्रात्मक संबंधों का अनुमान लगाएं
- परिणामों के सांख्यिकीय महत्व का परीक्षण करें
- निर्णय लेने में परिणामों का उपयोग
सरल प्रतिगमन के लिए सूत्र है -
Y = a + bX + u
Y= आश्रित चर
X= स्वतंत्र चर
a= अवरोधन
b= ढलान
u= यादृच्छिक कारक
क्रॉस सेक्शनल डेटा एक निश्चित समय पर संस्थाओं के समूह के बारे में जानकारी प्रदान करता है, जबकि समय श्रृंखला डेटा समय के साथ एक इकाई पर जानकारी प्रदान करता है। जब हम प्रतिगमन समीकरण का अनुमान लगाते हैं तो इसमें आश्रित और स्वतंत्र चर के बीच सबसे अच्छा रैखिक संबंध खोजने की प्रक्रिया शामिल होती है।
साधारण जानवर वर्गों की विधि (OLS)
साधारण से कम वर्ग विधि को बिंदुओं के बिखराव के माध्यम से एक रेखा को फिट करने के लिए डिज़ाइन किया गया है, इस तरह से लाइन से बिंदुओं के वर्ग विचलन का योग कम से कम किया जाता है। यह एक सांख्यिकीय पद्धति है। आमतौर पर सॉफ्टवेयर पैकेज OLS आकलन करते हैं।
Y = a + bX
निर्धारण का सह-कुशल (R 2 )
निर्धारण का सह-कुशल एक उपाय है जो निर्भर चर में भिन्नता के प्रतिशत को इंगित करता है जो स्वतंत्र चर में भिन्नता के कारण होता है। आर 2 फिट मॉडल की भलाई का एक उपाय है। निम्नलिखित तरीके हैं -
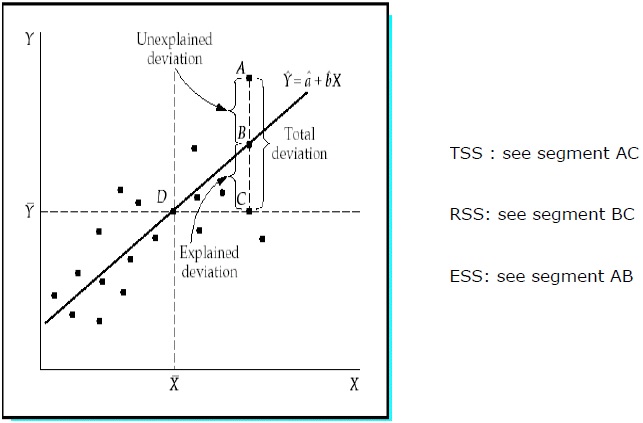
वर्गों का कुल योग (TSS)
Y के माध्य से Y के नमूना मूल्यों के वर्ग विचलन का योग।
TSS = SUM ( Yi − Y)2
Yi = आश्रित चर
Y = आश्रित चर का अर्थ
i = टिप्पणियों की संख्या
चौकों का प्रतिगमन योग (RSS)
वाई के मतलब से वाई के अनुमानित मूल्यों के वर्ग विचलन का योग।
RSS = SUM ( Ỷi − uY)2
Ỷi = Y का अनुमानित मूल्य
Y = आश्रित चर का अर्थ
i = विविधताओं की संख्या
वर्गों का त्रुटि योग (ESS)
वाई के अनुमानित मूल्यों से वाई के नमूना मूल्यों के वर्ग विचलन का योग।
ESS = SUM ( Yi − Ỷi)2
Ỷi = Y का अनुमानित मूल्य
Yi = आश्रित चर
i = टिप्पणियों की संख्या
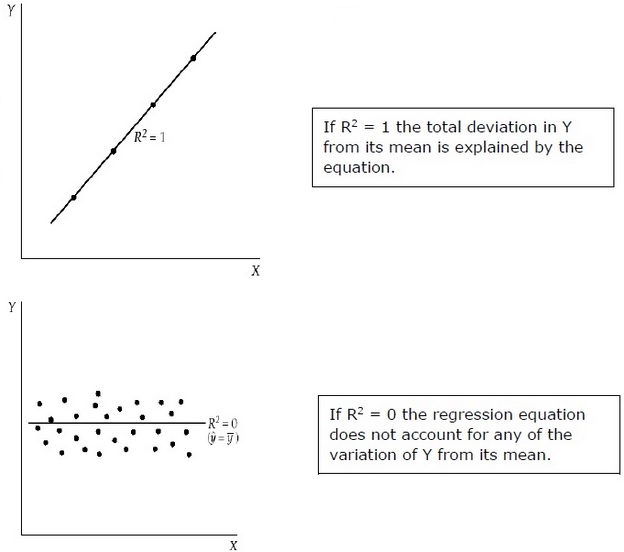
R 2 अपने माध्य से Y के कुल विचलन के अनुपात को मापता है जिसे प्रतिगमन मॉडल द्वारा समझाया गया है। R 2 एकता के करीब है, प्रतिगमन समीकरण की व्याख्यात्मक शक्ति जितनी अधिक होगी। एक आर 2 पास 0 इंगित करता है कि प्रतिगमन समीकरण में बहुत कम व्याख्यात्मक शक्ति होगी।
प्रतिगमन गुणांक के मूल्यांकन के लिए, जनसंख्या का एक नमूना पूरी आबादी के बजाय उपयोग किया जाता है। नमूने के आधार पर आबादी के बारे में धारणा बनाना और इन मान्यताओं के बारे में निर्णय लेना महत्वपूर्ण है।
प्रतिगमन गुणांक का मूल्यांकन
जनसंख्या का प्रत्येक नमूना अपना स्वयं का अवरोधन उत्पन्न करता है। सांख्यिकीय अंतर की गणना करने के लिए निम्नलिखित विधियों का उपयोग किया जा सकता है -
Two tailed test −
अशक्त परिकल्पना: एच 0 : बी = 0
वैकल्पिक परिकल्पना: एच ए : बी oth ०
One tailed test −
अशक्त परिकल्पना: H 0 : b> 0 (या b <0)
वैकल्पिक परिकल्पना: H a : b <0 (या b> 0)
Statistic Test −
बी = अनुमानित गुणांक
ई (बी) = बी = ० (शून्य परिकल्पना)
एसई बी = गुणांक की मानक त्रुटि
।का मूल्य tस्वतंत्रता की डिग्री, एक या दो असफल परीक्षण और महत्व के स्तर पर निर्भर करता है। के महत्वपूर्ण मूल्य का निर्धारण करने के लिएt, टी-टेबल का उपयोग किया जा सकता है। फिर महत्वपूर्ण मान के साथ टी-मूल्य की तुलना आती है। यदि कोई सांख्यिकीय परिकल्पना का निरपेक्ष मान महत्वपूर्ण टी-वैल्यू से अधिक या बराबर है, तो अशक्त परिकल्पना को अस्वीकार करने की आवश्यकता है। अशक्त परिकल्पना को अस्वीकार न करें, मैं सांख्यिकीय परीक्षण का निरपेक्ष मान महत्वपूर्ण t- मूल्य से कम है।
कई प्रतिगमन विश्लेषण
एकाधिक प्रतिगमन विश्लेषण में सरल प्रतिगमन के विपरीत, गुणांक निर्भर चर में परिवर्तन को इंगित करते हैं जो अन्य चर के मूल्यों को स्थिर मानते हैं।
सांख्यिकीय महत्व की परीक्षा को कहा जाता है F-test। एफ-परीक्षण उपयोगी है क्योंकि यह केवल एक व्यक्ति के बजाय पूरे प्रतिगमन समीकरण के सांख्यिकीय महत्व को मापता है। यहाँ शून्य परिकल्पना में, आश्रित चर और आबादी के स्वतंत्र चर के बीच कोई संबंध नहीं है।
सूत्र है - H 0 : b1 = b2 = b3 =…। = बीके = ०
आश्रित चर और के बीच कोई संबंध नहीं है k आबादी के लिए स्वतंत्र चर।
F-test static −
$$F \: =\: \frac{ \left ( \frac{R^2}{K} \right )}{\frac{(1-R^2)}{(n-k-1)}}$$
का महत्वपूर्ण मूल्य Fस्वतंत्रता और महत्व के स्तर के अंश और हर पर निर्भर करता है। एफ-टेबल का उपयोग महत्वपूर्ण एफ-मूल्य निर्धारित करने के लिए किया जा सकता है। महत्वपूर्ण मूल्य (F *) के साथ F-value की तुलना में -
यदि F> F *, हमें अशक्त परिकल्पना को अस्वीकार करने की आवश्यकता है।
यदि एफ <एफ *, शून्य परिकल्पना को अस्वीकार नहीं करते हैं क्योंकि निर्भर चर और सभी स्वतंत्र चर के बीच कोई महत्वपूर्ण संबंध नहीं है।