MATLAB - पथरी
MATLAB विभेदक और अभिन्न कलन की समस्याओं को हल करने के लिए, किसी भी डिग्री के अंतर समीकरणों को हल करने और सीमाओं की गणना के लिए विभिन्न तरीके प्रदान करता है। सबसे अच्छा, आप आसानी से जटिल फ़ंक्शन के ग्राफ़ को प्लॉट कर सकते हैं और मूल फ़ंक्शन, साथ ही इसके व्युत्पन्न को हल करके एक ग्राफ पर मैक्सिमा, मिनीमा और अन्य स्टेशनरी बिंदुओं की जांच कर सकते हैं।
यह अध्याय पथरी की समस्याओं से निपटेगा। इस अध्याय में, हम पूर्व-कैलकुलस अवधारणाओं पर चर्चा करेंगे अर्थात, कार्यों की सीमा की गणना और सीमाओं के गुणों का सत्यापन।
अगले अध्याय डिफरेंशियल में , हम एक अभिव्यक्ति के व्युत्पन्न की गणना करेंगे और एक ग्राफ पर स्थानीय मैक्सिमा और मिनीमा को पाएंगे। हम अंतर समीकरणों को हल करने पर भी चर्चा करेंगे।
अंत में, एकीकरण अध्याय में, हम अभिन्न कलन पर चर्चा करेंगे।
सीमा की गणना
MATLAB प्रदान करता है limitसीमा की गणना के लिए कार्य करते हैं। अपने सबसे बुनियादी रूप में,limit फ़ंक्शन अभिव्यक्ति को एक तर्क के रूप में लेता है और अभिव्यक्ति की सीमा को पाता है क्योंकि स्वतंत्र चर शून्य पर जाता है।
उदाहरण के लिए, चलिए एक फ़ंक्शन की सीमा की गणना करते हैं f (x) = (x 3 + 5) / (x 4 + 7), क्योंकि x शून्य हो जाता है।
syms x
limit((x^3 + 5)/(x^4 + 7))MATLAB उपरोक्त कथन को निष्पादित करेगा और निम्नलिखित परिणाम लौटाएगा -
ans =
5/7सीमा समारोह प्रतीकात्मक कंप्यूटिंग के दायरे में आता है; आप का उपयोग करने की जरूरत हैsymsMATLAB को बताने के लिए फ़ंक्शन करें कि आप किस प्रतीकात्मक चर का उपयोग कर रहे हैं। आप किसी फ़ंक्शन की सीमा की गणना भी कर सकते हैं, क्योंकि चर शून्य के अलावा कुछ संख्या में जाता है। X-> a (f (x)) की गणना करने के लिए , हम तर्कों के साथ सीमा कमांड का उपयोग करते हैं। पहला एक्सप्रेशन है और दूसरा नंबर है, वह एक्स एप्रोच है, यहाँ यह ए है ।
उदाहरण के लिए, हमें x (1) (x-3) = (x-1) के फलन की सीमा की गणना करते हैं, क्योंकि x 1 तक जाता है।
limit((x - 3)/(x-1),1)MATLAB उपरोक्त कथन को निष्पादित करेगा और निम्नलिखित परिणाम लौटाएगा -
ans =
NaNएक और उदाहरण लेते हैं,
limit(x^2 + 5, 3)MATLAB उपरोक्त कथन को निष्पादित करेगा और निम्नलिखित परिणाम लौटाएगा -
ans =
14ऑक्टेव का उपयोग करके सीमा की गणना
निम्नलिखित उपरोक्त उदाहरण का ऑक्टेव संस्करण है symbolic पैकेज, निष्पादित करने और परिणाम की तुलना करने की कोशिश करें -
pkg load symbolic
symbols
x = sym("x");
subs((x^3+5)/(x^4+7),x,0)ऑक्टेव उपरोक्त कथन को निष्पादित करेगा और निम्नलिखित परिणाम लौटाएगा -
ans =
0.7142857142857142857सीमाओं के बुनियादी गुणों का सत्यापन
बीजगणितीय सीमा प्रमेय सीमा के कुछ बुनियादी गुण प्रदान करता है। ये इस प्रकार हैं -
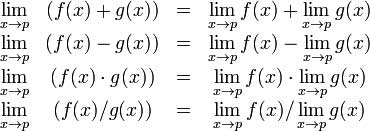
आइए हम दो कार्यों पर विचार करें -
- f (x) = (3x + 5) / (x - 3)
- g (x) = x 2 + 1।
आइए फ़ंक्शन की सीमाओं की गणना करें क्योंकि x दोनों कार्यों के 5 तक जाता है, और इन दो कार्यों और MATRAB का उपयोग करके सीमा के मूल गुणों को सत्यापित करता है।
उदाहरण
एक स्क्रिप्ट फ़ाइल बनाएँ और उसमें निम्न कोड टाइप करें -
syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)जब आप फ़ाइल चलाते हैं, तो यह प्रदर्शित होती है -
l1 =
17
l2 =
17
lAdd =
34
lSub =
0
lMult =
289
lDiv =
1ऑक्टेव का उपयोग करके सीमाओं के बुनियादी गुणों का सत्यापन
निम्नलिखित उपरोक्त उदाहरण का ऑक्टेव संस्करण है symbolic पैकेज, निष्पादित करने और परिणाम की तुलना करने की कोशिश करें -
pkg load symbolic
symbols
x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)ऑक्टेव उपरोक्त कथन को निष्पादित करेगा और निम्नलिखित परिणाम लौटाएगा -
l1 =
17.0
l2 =
17.0
lAdd =
34.0
lSub =
0.0
lMult =
289.0
lDiv =
1.0लेफ्ट और राइट साइडेड लिमिट
जब किसी फ़ंक्शन में वैरिएबल के कुछ विशेष मूल्य के लिए एक छूट होती है, तो सीमा उस बिंदु पर मौजूद नहीं होती है। दूसरे शब्दों में, किसी फ़ंक्शन f (x) की सीमा में x = a पर असंतोष है, जब सीमा का मान, जैसा कि x बाईं ओर से x के समीप आता है, तो सीमा का मान उतना नहीं होता जितना x दाईं ओर से आता है।
यह बाएं हाथ और दाहिने हाथ की सीमाओं की अवधारणा की ओर जाता है। एक बाएं हाथ की सीमा को x -> a के रूप में सीमा के रूप में परिभाषित किया गया है, यानी x <a के मान के लिए, x, a के पास जाता है। एक दाएं हाथ की सीमा को x -> a के रूप में सीमा के रूप में परिभाषित किया गया है, यानी, x, a के मान के लिए, x ए के पास जाता है। जब बाएं हाथ की सीमा और दाहिने हाथ की सीमा बराबर नहीं होती है, तो सीमा मौजूद नहीं होती है।
आइए एक समारोह पर विचार करें -
f(x) = (x - 3)/|x - 3|
हम दिखाएंगे कि लिम x-> 3 f (x) मौजूद नहीं है। MATLAB इस तथ्य को दो तरीकों से स्थापित करने में हमारी मदद करता है -
- फ़ंक्शन के ग्राफ को साजिश रचने और असंगतता दिखाने के द्वारा।
- सीमा की गणना करके और दिखाते हैं कि दोनों अलग हैं।
बाएं और दाएं हाथ की सीमा की गणना अंतिम तर्क के रूप में सीमा के कमांड के 'लेफ्ट' और 'राइट' को पास करके की जाती है।
उदाहरण
एक स्क्रिप्ट फ़ाइल बनाएँ और उसमें निम्न कोड टाइप करें -
f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')जब आप फ़ाइल चलाते हैं, तो MATLAB निम्नलिखित प्लॉट को आकर्षित करता है
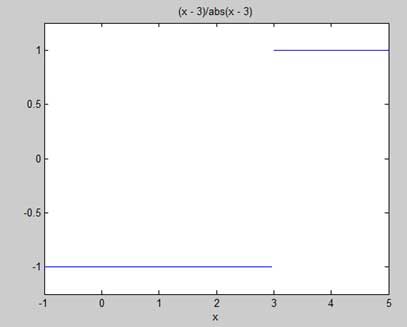
इसके बाद निम्न आउटपुट प्रदर्शित किया जाता है -
l =
-1
r =
1