MATLAB - एकीकरण
एकीकरण दो अनिवार्य रूप से विभिन्न प्रकार की समस्याओं से संबंधित है।
पहले प्रकार में, एक फ़ंक्शन का व्युत्पन्न दिया जाता है और हम फ़ंक्शन को ढूंढना चाहते हैं। इसलिए, हम मूल रूप से भेदभाव की प्रक्रिया को उल्टा करते हैं। इस रिवर्स प्रक्रिया को एंटी-डिफरेंशियल के रूप में जाना जाता है, या आदिम फ़ंक्शन को खोजने, या खोजने के लिएindefinite integral।
दूसरी प्रकार की समस्याओं में बहुत बड़ी मात्रा में बहुत अधिक मात्राएँ शामिल होना और फिर मात्राओं के आकार को शून्य तक ले जाना एक सीमा होती है, जबकि शब्दों की संख्या अनन्तता तक होती है। इस प्रक्रिया की परिभाषा की ओर जाता हैdefinite integral।
निश्चित इंटीग्रल्स का उपयोग क्षेत्र, वॉल्यूम, गुरुत्वाकर्षण के केंद्र, जड़ता के क्षण, एक बल द्वारा किए गए काम और कई अन्य अनुप्रयोगों में खोजने के लिए किया जाता है।
MATLAB का उपयोग करते हुए अनिश्चितकालीन इंटीग्रल ढूँढना
परिभाषा के अनुसार, यदि किसी फ़ंक्शन f (x) का व्युत्पन्न f '(x) है, तो हम कहते हैं कि x के संबंध में f' (x) का अनिश्चितकालीन इंटीग्रेशन f (x) है। उदाहरण के लिए, चूंकि x 2 का व्युत्पन्न (x के संबंध में) 2x है, इसलिए हम कह सकते हैं कि 2x का अनिश्चितकालीन अभिन्न x 2 है ।
प्रतीकों में -
f'(x2) = 2x, इसलिए,
∫ 2xdx = x2.
अनिश्चित इंटीग्रल अद्वितीय नहीं है, क्योंकि एक स्थिर सी के किसी भी मूल्य के लिए x 2 + c का व्युत्पन्न , 2x भी होगा।
इसे प्रतीकों में व्यक्त किया गया है -
∫ 2xdx = x2 + c।
जहाँ, c को 'मनमाना स्थिरांक' कहा जाता है।
MATLAB एक प्रदान करता है intएक अभिव्यक्ति के अभिन्न गणना के लिए आदेश। किसी फ़ंक्शन के अनिश्चितकालीन अभिन्न के लिए एक अभिव्यक्ति प्राप्त करने के लिए, हम लिखते हैं -
int(f);उदाहरण के लिए, हमारे पिछले उदाहरण से -
syms x
int(2*x)MATLAB उपरोक्त कथन को निष्पादित करता है और निम्नलिखित परिणाम देता है -
ans =
x^2उदाहरण 1
इस उदाहरण में, आइए हम कुछ सामान्य रूप से प्रयुक्त अभिव्यक्तियों के अभिन्न का पता लगाएं। एक स्क्रिप्ट फ़ाइल बनाएँ और उसमें निम्न कोड टाइप करें -
syms x n
int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)जब आप फ़ाइल चलाते हैं, तो यह निम्न परिणाम प्रदर्शित करता है -
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)उदाहरण 2
एक स्क्रिप्ट फ़ाइल बनाएँ और उसमें निम्न कोड टाइप करें -
syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))ध्यान दें कि pretty फ़ंक्शन अधिक पठनीय प्रारूप में एक अभिव्यक्ति देता है।
जब आप फ़ाइल चलाते हैं, तो यह निम्न परिणाम प्रदर्शित करता है -
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2MATLAB का उपयोग करके निश्चित इंटीग्रल ढूँढना
परिभाषा के अनुसार, निश्चित अभिन्न मूल रूप से एक राशि की सीमा है। हम निश्चित अभिन्न का उपयोग करते हैं जैसे कि वक्र और x- अक्ष के बीच का क्षेत्र और दो घटता के बीच का क्षेत्र। निश्चित अभिन्न का उपयोग अन्य स्थितियों में भी किया जा सकता है, जहां आवश्यक मात्रा को राशि की सीमा के रूप में व्यक्त किया जा सकता है।
int जिस सीमा पर आप अभिन्न की गणना करना चाहते हैं, उसे पारित करके निश्चित एकीकरण के लिए फ़ंक्शन का उपयोग किया जा सकता है।
की गणना करना
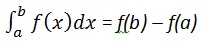
हम लिखते हैं,
int(x, a, b)उदाहरण के लिए,

int(x, 4, 9)MATLAB उपरोक्त कथन को निष्पादित करता है और निम्नलिखित परिणाम देता है -
ans =
65/2उपरोक्त गणना के बराबर ऑक्टेव निम्नलिखित है -
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));ऑक्टेव कोड निष्पादित करता है और निम्नलिखित परिणाम लौटाता है -
Area:
32.500ऑक्टेव द्वारा दिए गए क्वाड () फ़ंक्शन का उपयोग करके एक वैकल्पिक समाधान दिया जा सकता है -
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));ऑक्टेव कोड निष्पादित करता है और निम्नलिखित परिणाम लौटाता है -
Area:
32.500उदाहरण 1
आइए एक्स-एक्सिस और वक्र y = x 3 the2x + 5 के बीच संलग्न क्षेत्र की गणना करें और x = 1 और x = 2 का निर्देशन करें।
आवश्यक क्षेत्र इसके द्वारा दिया गया है -
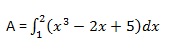
एक स्क्रिप्ट फ़ाइल बनाएँ और निम्न कोड टाइप करें -
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));जब आप फ़ाइल चलाते हैं, तो यह निम्न परिणाम प्रदर्शित करता है -
a =
23/4
Area:
5.7500उपरोक्त गणना के बराबर ऑक्टेव निम्नलिखित है -
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));ऑक्टेव कोड निष्पादित करता है और निम्नलिखित परिणाम लौटाता है -
Area:
5.7500ऑक्टेव द्वारा दिए गए क्वाड () फ़ंक्शन का उपयोग करके एक वैकल्पिक समाधान दिया जा सकता है -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));ऑक्टेव कोड निष्पादित करता है और निम्नलिखित परिणाम लौटाता है -
Area:
5.7500उदाहरण 2
वक्र के नीचे का क्षेत्रफल ज्ञात करें: f (x) = x 2 cos (x) ≤4 ≤ x। 9 के लिए।
एक स्क्रिप्ट फ़ाइल बनाएँ और निम्नलिखित कोड लिखें -
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));जब आप फ़ाइल चलाते हैं, तो MATLAB ग्राफ़ को प्लॉट करता है -
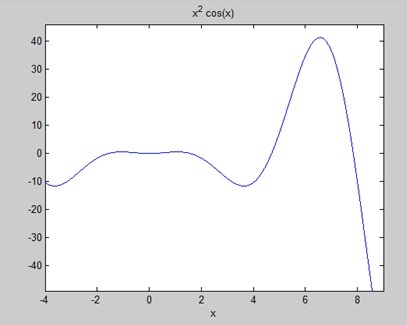
उत्पादन नीचे दिया गया है -
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326उपरोक्त गणना के बराबर ऑक्टेव निम्नलिखित है -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));